![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/丸い三角関数』として書籍化されています。
放課後の図書室。 高校二年生の僕は、後輩のテトラちゃんに $\sin$ と $\cos$ について話している。
僕「$\sin$(サイン)の覚え方として有名なのはこれだよね。筆記体のsを使って《$c$ 分の $b$》という順に分数を作る。sは $\sin$ のsだよ。 《$\sin$ は、 $\theta$ から $\dfrac{b}{c}$ を求める関数》といえるんだ」
$\sin \theta$ の覚え方
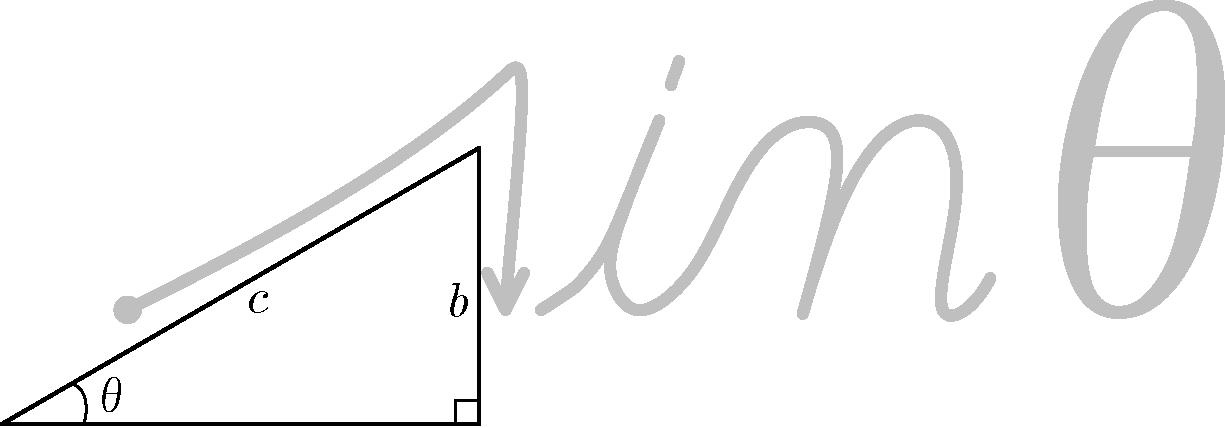
テトラ「ここまで、よくわかりましたっ!」
僕「そして、次にやることは $0^{\circ} < \theta < 90^{\circ}$ の制限を外すことだ」
テトラ「制限を……外す?」
僕「そうだよ。ほら角度 $\theta$ に制限がついているとやっかいだから」
テトラ「あたし、よくそういう制限や条件を忘れるんです……」
僕「角度 $\theta$(シータ)に、 $0^{\circ} < \theta < 90^{\circ}$ という制限がついちゃった理由はわかるよね。 直角三角形を使って $\sin$ を定義したから」
テトラ「はい」
僕「だからね、僕たちはこれから円を使って $\sin$ を定義する」
テトラ「円で三角関数を定義するんですか?」
僕「そうだよ」
テトラ「……ということは、 $\sin$ には二種類あるんですか?」
僕「二種類って?」
テトラ「直角三角形で定義する $\sin$ と、円で定義する $\sin$ と……」
僕「あ、いやいや、そういうわけじゃないよ。 円で定義した $\sin$ も、 $0^{\circ} < \theta < 90^{\circ}$ の範囲では 直角三角形で定義したものとまったく一致するから」
テトラ「はあ……なんだか難しそうです」
僕「いやいや、そんなに難しくはないから大丈夫。このように決めましょうという約束の話だけだよ」
テトラ「はい……」
僕「じゃ、最初に復習しておこうか。これまで僕たちは $\sin$ を直角三角形の二辺の比で定義していた。分数だね」
直角三角形の辺の比で $\sin \theta$ を定義する($0^{\circ} < \theta < 90^{\circ}$)
$$ \sin \theta = \dfrac{b}{c} $$
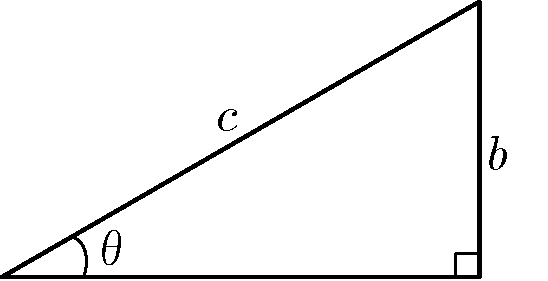
テトラ「はい、そうでした」
僕「ここでは二辺の比、つまり $\dfrac{b}{c}$ の値が重要なんだから、 $c$ の長さを $1$ として考えることにしよう。 直角三角形の各辺を $c$ 分の $1$ にしたと思ってもいいよ」
テトラ「どうしてそういうことをするんですか?」
僕「そうすると、 $\sin \theta = \dfrac{b}{c} = \dfrac{b}{1} = b$ だから、式が簡単になるよね」
テトラ「あ、はい。そうですね」
僕「それに、 $\sin \theta = b$ ということは三角形の一辺がちょうど $\sin$ の値になるし」
直角三角形の辺の比で $\sin \theta$ を定義する($0^{\circ} < \theta < 90^{\circ}$)
$$ \sin \theta = b \qquad \REMTEXT{($c = 1$とした場合)} $$
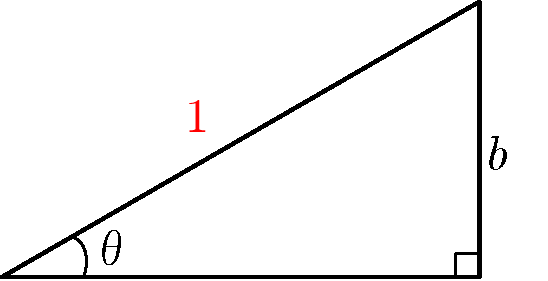
僕「直角三角形の $\theta$ がある頂点を、座標平面の原点の上に置いて、直角は $x$ 軸の上。そして、残った頂点に $P$ という名前をつけるよ」
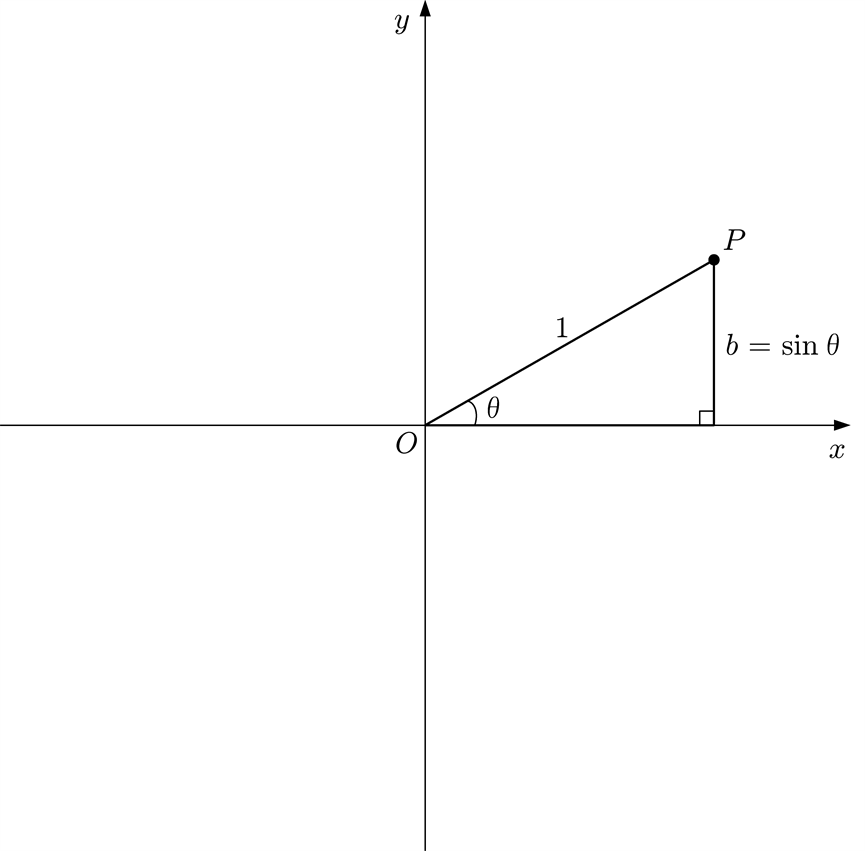
テトラ「……」
僕「このとき、 $c = 1$ と決めているから、頂点 $P$ の《高さ》が $\sin \theta$ になるよね」
テトラ「高さ?」
僕「うん、座標平面で、 $x$ 軸からどれだけ上にあるかということ」
テトラ「あ、はいはい。わかりました」
僕「じゃあ、クイズを出すね。 この図で $\theta$ を変化させると、頂点 $P$ はどんな図形を描くかわかる?」
クイズ
角 $\theta$ を変化させると、頂点 $P$ はどんな図形を描くか。 ただし、点 $O$ と点 $P$ の距離は常に $1$ に等しいとする。

テトラ「どんな図形を描くか? ……すみません。あの、まるい、円ですか?」
僕「そうだよ、円だね。 $O$ と $P$ の距離が $1$ で固定されているから、 $\theta$ を変化させると、 コンパスでぐるっと円を描くような感じになるね」
テトラ「そうですね」
僕「ところで、テトラちゃん……別に《すみません》なんて、あやまる必要はないんだよ」
テトラ「あ、はい!」
クイズの答え
角 $\theta$ を変化させると、頂点 $P$ は円を描く。
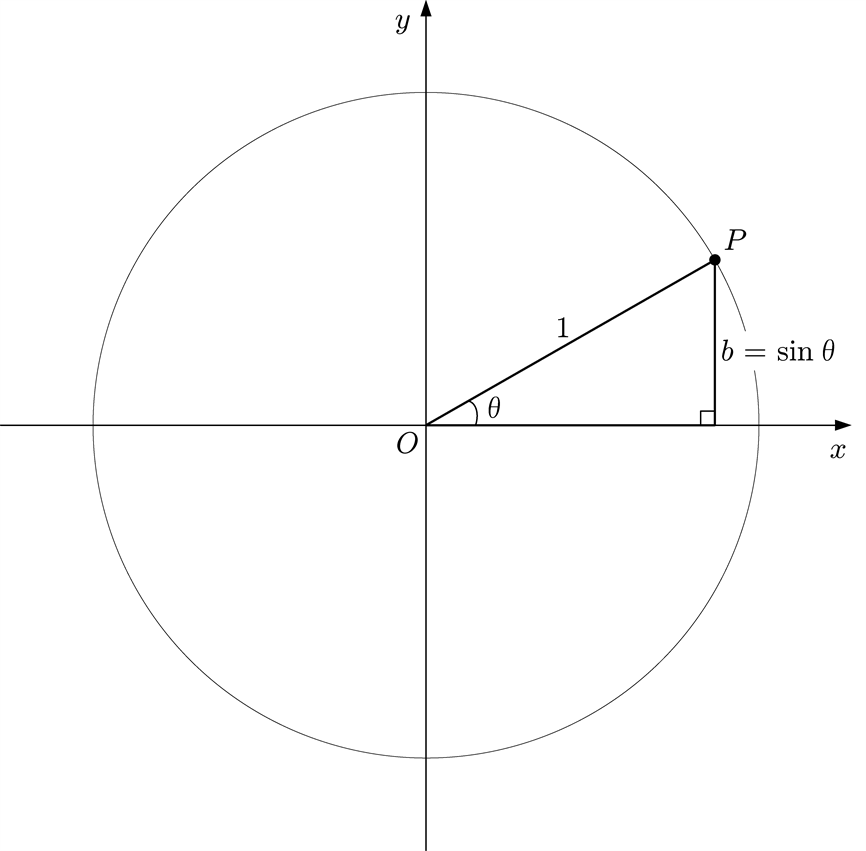
僕「この円のような、半径が $1$ の円のことを単位円っていうんだよ。 この図は特に、原点を中心にした単位円になるね」
テトラ「単位円……と」
テトラちゃんは《秘密ノート》に用語をメモする。
僕「円が出てきたところで、僕たちは直角三角形に縛られるのをやめる」
テトラ「あたしたち、直角三角形に縛られてたんですか?」
僕「そうだよ。だって、僕たちは $\sin \theta$ を直角三角形で定義してたからね。 たとえば、 $\theta = 0^\circ$ になったら、直角三角形は作れないから困ってしまう」
テトラ「あ! 角度が $0^\circ$ だと、直角三角形がぺちゃんとつぶれちゃうからですか」
僕「そうそう。そういうこと。 円を使って $\sin \theta$ を定義するときは、《$\sin \theta$ は点 $P$ の $y$ 座標である》と定める」
テトラ「点 $P$ の $y$ 座標……」
僕「図で見ればすぐわかると思うよ」
単位円上の点 $P$ の $y$ 座標で $\sin \theta$ を定義する
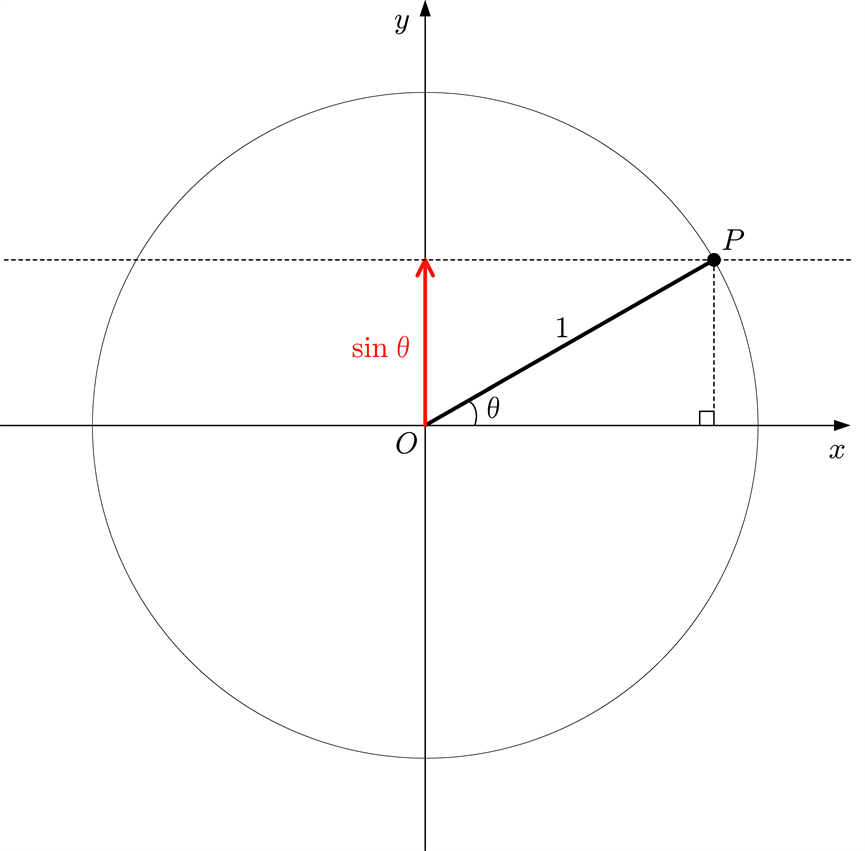
テトラ「……」
僕「この定義だと、 $0^{\circ} < \theta < 90^{\circ}$ の範囲での $\sin \theta$ の値は、 直角三角形で定義したものとまったく一致するのはわかるよね」
テトラ「は、はい。だって、直角三角形が《見え》ますし!」
僕「そうそう」
テトラ「ははあ……やっと先輩のおっしゃる《高さ》というのがわかってきました」
僕「点 $P$ の位置によってはその《高さ》はマイナスになるから、ちょっと注意が必要だけどね」
テトラ「マイナスですか?」
僕「うん、そうだよ。 $\theta$ の値によっては、 $\sin \theta < 0$ になることがあるということ。たとえばこの例のように」
$\sin \theta < 0$ になる例
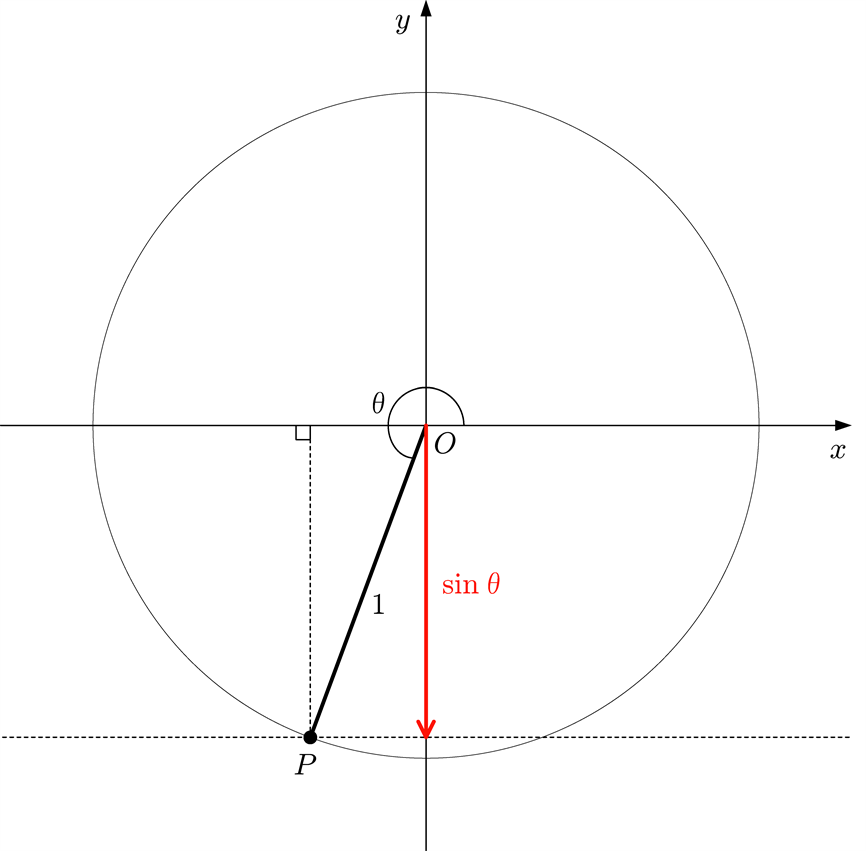
テトラ「なるほど! 下にこう……もぐっちゃうんですね」
僕「$\theta$ の値を少しずつ大きくしたグラフを描いてみればよくわかるよ」
$\theta = 0^\circ, 30^\circ, 60^\circ, 90^\circ$
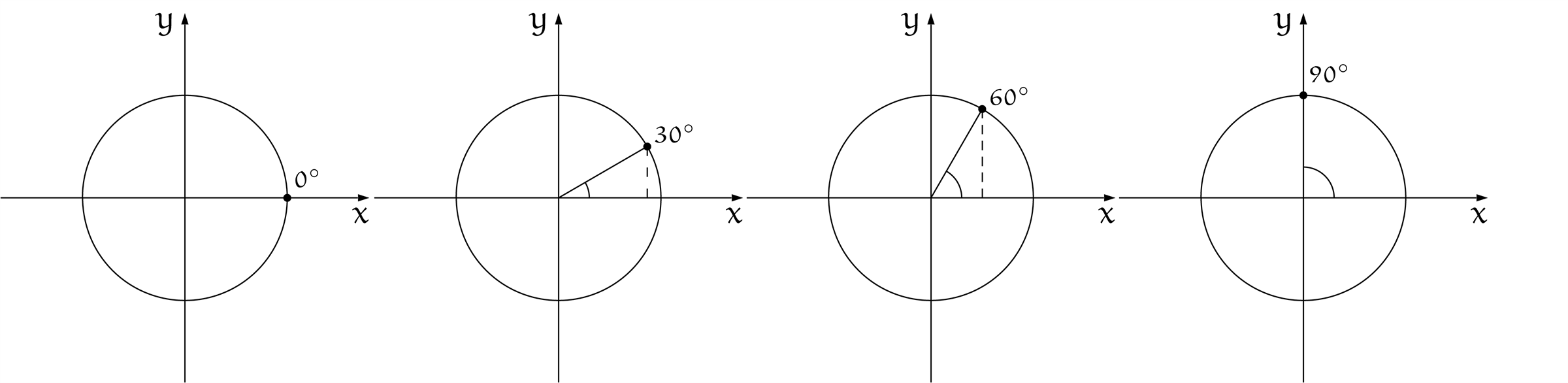
$\theta = 90^\circ, 120^\circ, 150^\circ, 180^\circ$
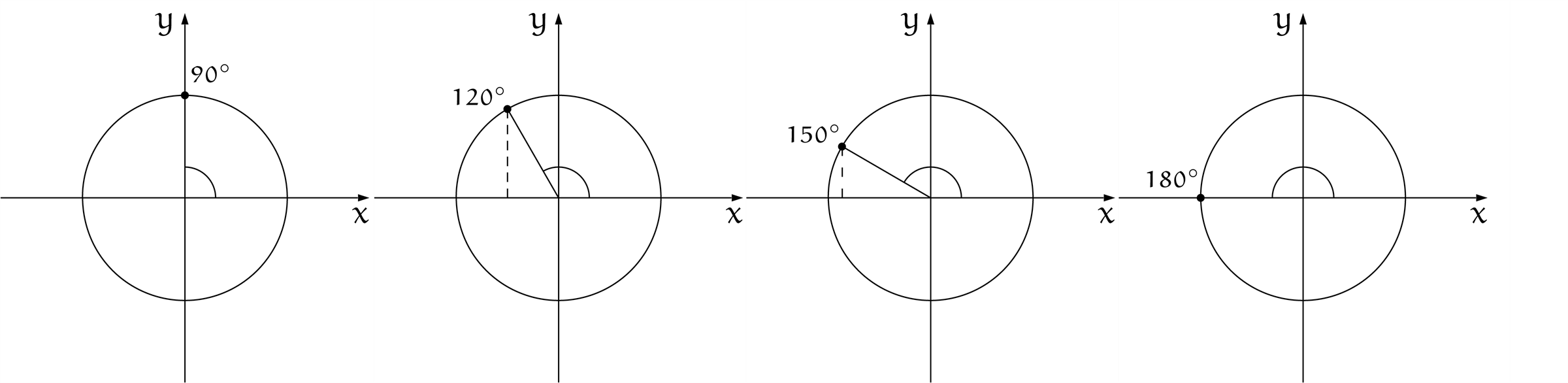
$\theta = 180^\circ, 210^\circ, 240^\circ, 270^\circ$
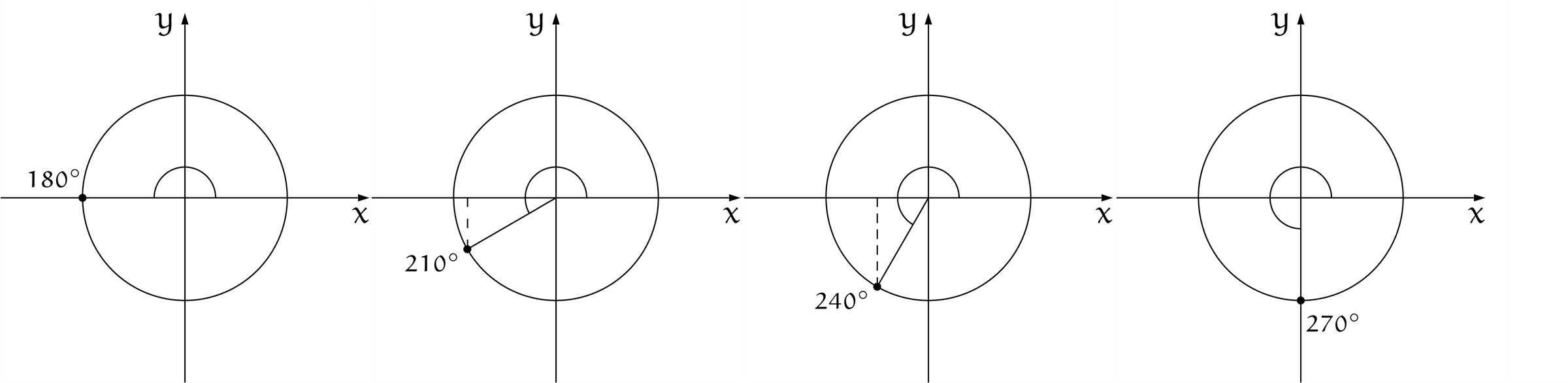
$\theta = 270^\circ, 300^\circ, 330^\circ, 360^\circ$
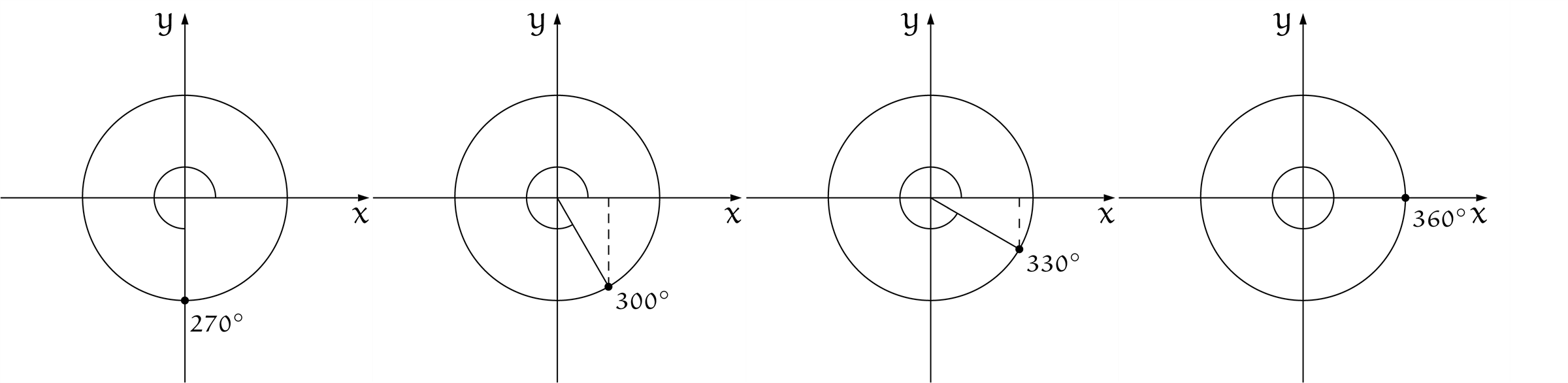
単位円の円周上、点を $30^\circ$ ずつ回転させた
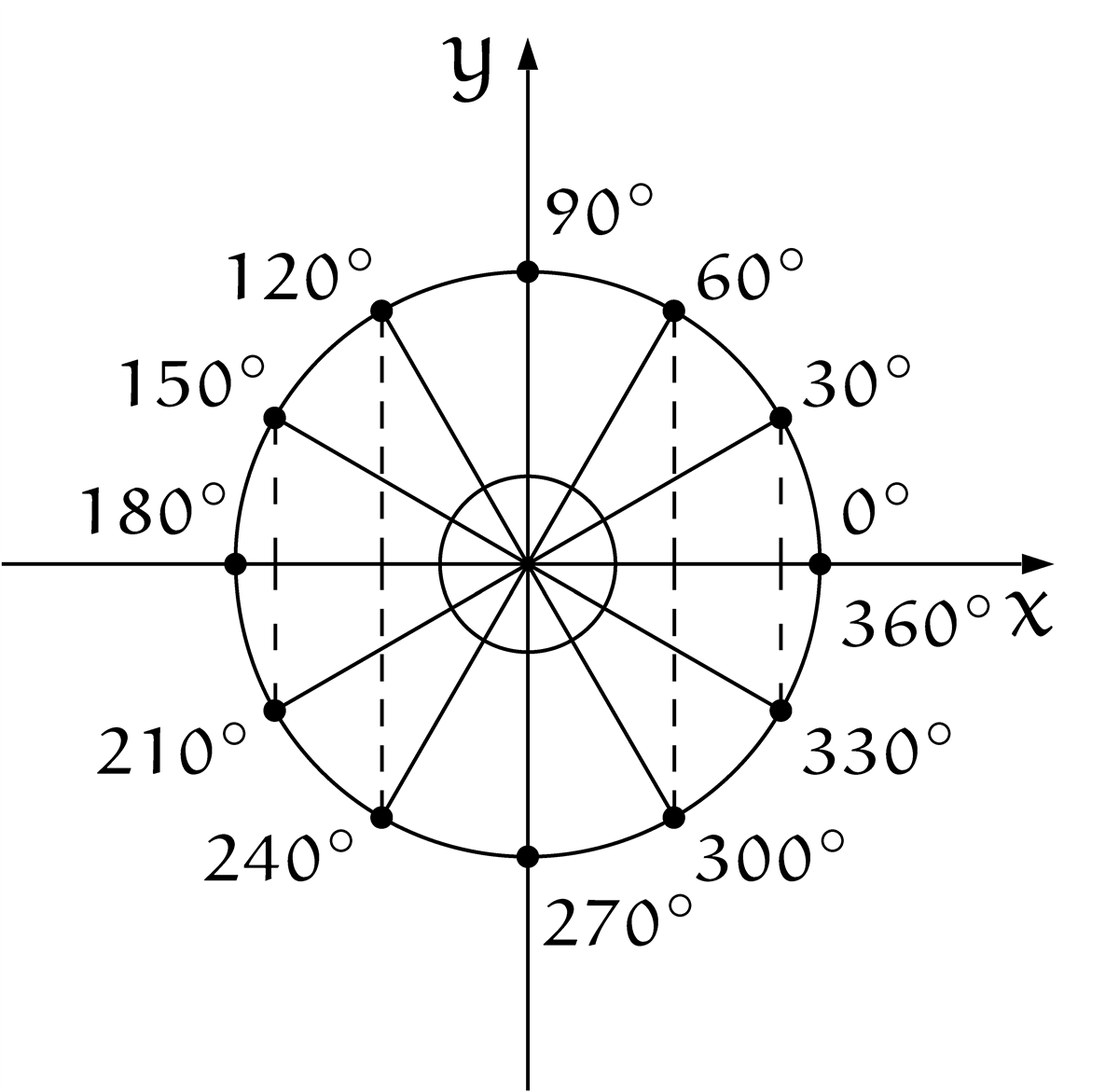
テトラ「なるほど……あっ! 先輩! あの、もしかして、こういう式って、成り立ちますか?」
$$ -1 \leq \sin \theta \leq 1 $$僕「いいね、テトラちゃん! その通りだよ。どうしてそう思ったの?」
テトラ「だって、この円は半径が $1$ ですから、円のいちばん《上》の $y$ 座標は $1$ で、 いちばん《下》の $y$ 座標は $-1$ ですよね。 そして、点 $P$ の $y$ 座標が $\sin \theta$ なので、 $\sin \theta$ は、 $-1$ 以上で $1$ 以下の範囲に入っているはずですっ!」
僕「そうそう、その発見はいいなあ、テトラちゃん! どんな角度 $\theta$ に対しても、 $-1 \leq \sin \theta \leq 1$ が成り立つ。これは $\sin \theta$ の定義からわかる $\sin \theta$ の性質だね」
テトラ「はいっ!」
ミルカ「楽しそうだな」
テトラ「あ、ミルカさん! いま先輩から $\sin$ について教わっていたんです!」
ミルカさんさんは長い黒髪、メタルフレームの眼鏡をした才媛だ。 放課後には僕やテトラちゃんといっしょに数学トークをする。
ミルカ「ふうん……サインカーブはこれからか」
テトラ「サインカーブ……といいますと?」
ミルカさんは、テトラちゃんの隣に座る。 僕の手からナチュラルにシャーペンを奪い、 テトラちゃんに説明を始めた。 クールな様子をしているけれど、 僕にはわかる。 ミルカさんは、サインカーブの説明をしたくてうずうずしているんだ。
ミルカ「テトラ、単位円を置いている座標平面の横軸は何?」
テトラ「横軸は……えっと、 $x$ 軸ですか?」
ミルカ「そう。だから、この単位円上の点の座標を $(x, y)$ とおくと、 この円というグラフは $x$ と $y$ が満たす関係を表現している」
僕「制約だね」
テトラ「あ、はい、そうですね。以前、 $2$ 次関数で放物線を描いたときもそうでした」
ミルカ「この座標平面の右に《横軸を $\theta$ 軸にしたグラフ》を描く。縦軸は $y$ 軸のままだ」
テトラ「横軸を $\theta$ 軸にしたグラフ……」
僕「グラフでは縦軸と横軸が大切だからね、ミルカさん」
ミルカさんは軽く頷いてすぐに話を続ける。ほんとに楽しそうだ。
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 420本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2013年3月29日)
この記事は『数学ガールの秘密ノート/丸い三角関数』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!