![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/微分を追いかけて』として書籍化されています。
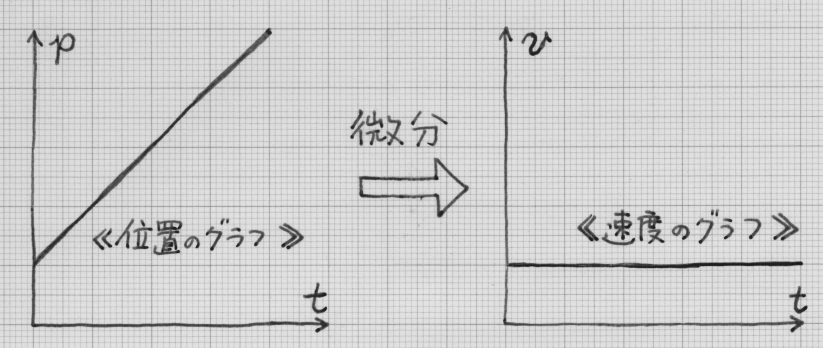
僕「このように《位置のグラフ》から《速度のグラフ》を得ること。これが微分なんだ」
ユーリ「えええ? なにそれ急に」
僕「うん。びっくりするよね」
高校生の僕は、中学生のユーリに《位置のグラフ》と《速度のグラフ》を使って、微分を説明しようとしている。
ユーリ「びっくりするってゆーか……それだけのこと?」
僕「それだけのことだよ。もちろん、いま言った《位置のグラフ》から《速度のグラフ》を得るというのは、 微分の定義じゃなくて、微分の例なんだけどね。 定義を正確に説明するためには数学的な準備が必要だから、速度の例でまずは感覚的にわかってほしいと思って」
ユーリ「例……といっても、《位置のグラフ》から《速度のグラフ》を得ることは微分なんでしょ?」
僕「そうだよ。もうちょっと正確にいうなら『《位置のグラフ》を時間で微分すると《速度のグラフ》が得られる』になるかな」
ユーリ「え? いまお兄ちゃんが言ったこと、さっき言ったことと何か違う?」
僕「違うよ。さっきはただ《微分》と言ったけど、いまは《時間で微分》と言った」
ユーリ「じかんでびぶん……」
僕「うん、そう。《微分する》というときは《何で》微分するのかをいわないと意味がない。 ただ、速度の話をするときには必ず時間で微分することになるから、 さぼって『《位置のグラフ》を微分すると《速度のグラフ》が得られる』といっても間違いじゃないけど」
《位置のグラフ》と《速度のグラフ》
《位置のグラフ》を時間で微分すると《速度のグラフ》が得られる。
ユーリ「お兄ちゃんの話を聞いてると、何だか国語の勉強しているみたい」
僕「え、どうして?」
ユーリ「だって、言葉の使い方うるさいんだもん。位置でしょ、速度でしょ、時間でしょ……それから速度の大きさが速さ。 時間で微分する……」
僕「それはそうだね。国語の勉強というか、用語をていねいに使うのは数学で大切なこと。 なぜかというと」
ユーリ「あれ! お兄ちゃん、おかしいよ!」
僕「……何が?」
ユーリ「あのね。速度って理科で勉強するじゃん。でも微分は数学? 理科みたいな数学みたいな国語? 変なの」
僕「ユーリは、なかなかいいところに気づいたなあ。 理科……ここでは理科の中でも特に物理学だね。 数学は物理学で学ぶいろんな現象をうまく表現する言葉だといってもいい。 だから、ユーリがいま言ったみたいに、理科みたいな数学みたいな国語という感覚は正しい。 とても正しい。だって、もともと学校で習う科目っていうのは便宜的に分けたものだからね」
ユーリ「ベンギテキ?」
僕「科目を分けて勉強した方が教えやすいし学びやすいから、都合上たまたまそうしているってこと」
ユーリ「ふーん」
僕「数学で学ぶ数式は、二つの量の関係を表したりグラフに描いたりするときに便利だよね。 だから、物理学で、ものが動き回る様子を表すために数学……特に数式やグラフを使うのはとても自然なことだよ」
ユーリ「なるほどー」
僕「いまお兄ちゃんがやっているのは逆だけどね」
ユーリ「逆って?」
僕「だからね、物理学のことを研究するために微分を使うんじゃなくて、 微分を説明するために物理学の速度の話を使っているということ」
ユーリ「ほーほー」
僕「話を戻すけど、動く点……動点が一定の速度で位置を変えているときは、 微分がどうこうといっても、変化がないからあまりおもしろくない」
ユーリ「うんうん」
僕「微分がおもしろくなるのは、動点が速度を変えるときだね。 じゃあ、また《位置のグラフ》から考えてみることにしよう」
ユーリ「うん!」
僕「ある直線上を動いている動点の位置が、 この《位置のグラフ》のように変化したとしよう。 このときの《速度のグラフ》を作るのが僕たちのやりたいこと」
《位置のグラフ》の例
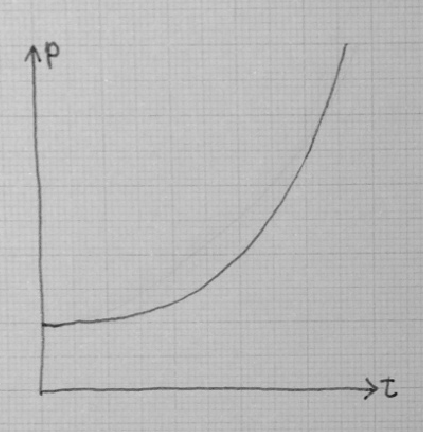
ユーリ「《位置のグラフ》がまっすぐじゃない」
僕「そうだね。直線じゃない」
ユーリ「ぐいーんと速くなってる」
僕「その通り。その《ぐいーん》を数学的に表現すれば《速度のグラフ》になるわけだ」
ユーリ「ねー、ユーリも《位置のグラフ》描いていい?」
僕「いいよいいよ。いくらでも」
ユーリ「あのね、この《位置のグラフ》を見ると、この場所とこの場所で……」
僕「ユーリ、何か文字を書いたほうが説明しやすいよ」
ユーリ「あ、そかそか。……描いたよ。この $A$ の場所だと上にちょっとしか進まない。でも $B$ の場所だと上にすごく進む。 だから、 $B$ のほうが速度が速いんだよ」
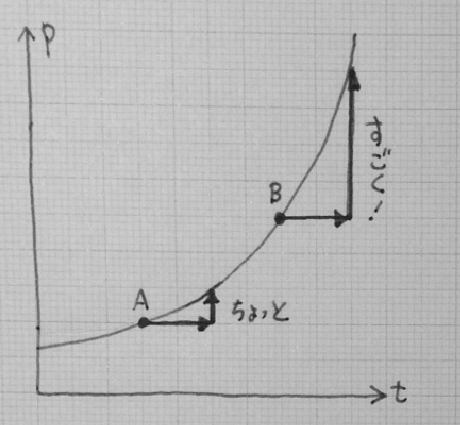
僕「いいね! ユーリのその読み方はとてもいい。《位置のグラフ》をちゃんと読んでる。 でも『速度が速い』は『速度が大きい』と言ったほうがいいよ」
ユーリ「わかった……だから、 $A$ よりも $B$ の場所のほうが速度が大きい」
僕「その通り。いまユーリが描いた《L字》みたいな形を取りだしてみるとよくわかるね」
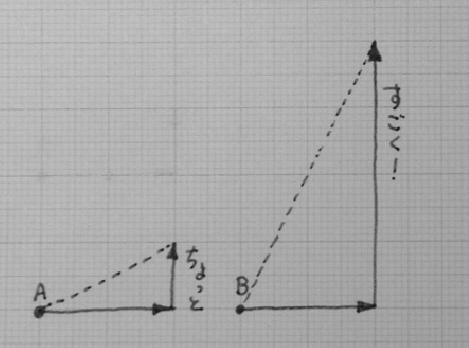
ユーリ「そーそー、エル字の逆だけど、右におんなじだけ進んだときに上に進む大きさが違うんでしょ?」
僕「うん、速度の定義と見比べるとよくわかるね。速度の定義は、いろんな書き方があるけど、たとえばこうだった」
速度の定義
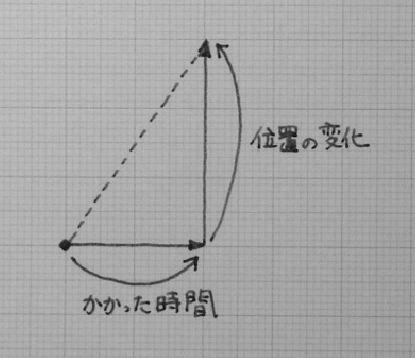
$$ \begin{align*} \REMTEXT{速度} &= \frac{\REMTEXT{位置の変化}}{\REMTEXT{かかった時間}} \\ &= \frac{\REMTEXT{変化後の位置} - \REMTEXT{変化前の位置}}{\REMTEXT{変化後の時刻} - \REMTEXT{変化前の時刻}} \\ \end{align*} $$
ユーリ「……」
僕「さっきのL字形で言えば、《かかった時間》は右に進んだ大きさで、《位置の変化》は上に進んだ大きさになる」
ユーリ「ふんふん」
僕「さっき手書きした《位置のグラフ》から《速度のグラフ》を作ろうとするなら、 《位置のグラフ》上にたくさん点を取ってL字形をたくさん作って割り算をすればいい」
ユーリ「うんうん、そうだね。こーゆー感じ?」
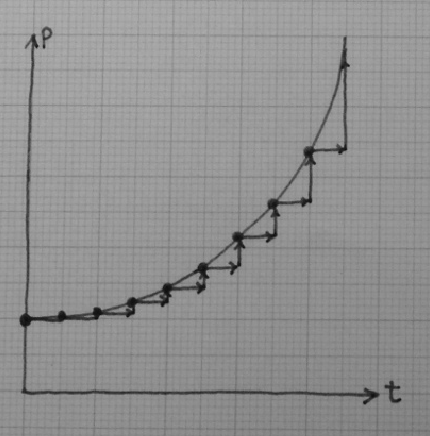
僕「そうなる。そして、これに対する《速度のグラフ》はこうなる」
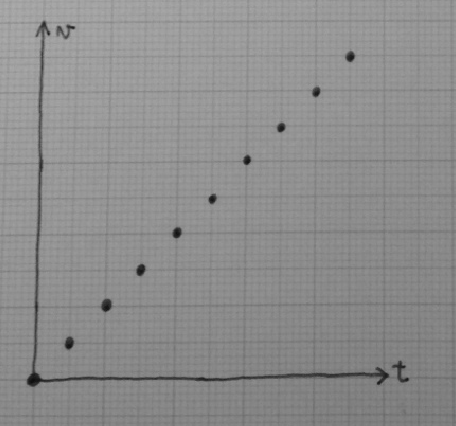
ユーリ「え……でも、こんなにうまい具合に直線に並ぶとは限らないんじゃない?」
僕「そうだね。いまは手描きで《位置のグラフ》を作ったから、これがどんな《速度のグラフ》になるかは、 実際に一つ一つ計算しなくちゃわからないね」
ユーリ「ふーん……」
僕「ところでユーリ。ここで問題が出てくる」
ユーリ「え?」
僕「速度が一定なら問題にならなかったことなんだけどね。 いまL字形を描いて計算していくと、《速度のグラフ》はテンテンでしか描けない。 なぜなら、L字形の時刻で、L字形の横幅の時間がかかった分の速度しかわからないから」
ユーリ「そりゃそーだ。あ、でもエルの横幅を狭くして、たくさんのエルを作ればいーじゃん。めんどくさいけど」
僕「それは一つの方法ではある。横幅を狭くすればテンテンの間隔も細かくなるし、《速度のグラフ》はそれだけ正確になる」
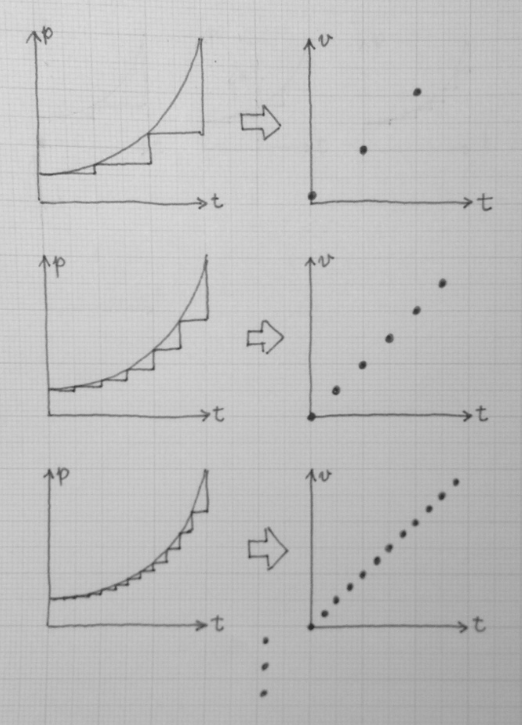
ユーリ「……」
僕「さあ、ユーリ。これでやっとお兄ちゃんが説明したいところまで来た。ここで微分の」
ユーリ「ちょっと待って! お兄ちゃん!」
僕「がく。どうした?」
ユーリ「ユーリ、わかんなくなった」
ユーリ「エルの横幅を狭くすればするほど正確になるってほんと? だってすごく狭くしたらエルの縦がゼロになっちゃうんじゃない?」
僕「いやいや。《エルの横幅を狭くする》っていうのをもう少し正確に話そう。 ユーリが言うのは、《位置のグラフ》の上にたくさん点を取ってエルを作るときに、 《かかった時間》の横幅を狭くするという話だよね」
ユーリ「そう。でもね、そんなことしたら、上に進む量がすごく小さくなって、ゼロになっちゃわない?」
僕「うん、《かかった時間》をすごくすごく小さくしたら《位置の変化》もすごくすごく小さくなる。 でも、僕たちがいま注目しているのは、《位置の変化》じゃなくて、《速度》だ。 速度は《位置の変化》を《かかった時間》で割ったものだった」
ユーリ「だから、なに?」
僕「だから、《位置の変化》がすごく小さくなっても、《かかった時間》のほうもそれに合わせてすごく小さくなれば、 割り算の結果はそう簡単にはゼロにはならないんだよ」
ユーリ「……こーゆーこと?《かかった時間》を $1$ 秒間隔じゃなくて、 $0.1$ 秒にしたとき、《位置の変化》も十分の一になればいいでしょ、ってこと?」
僕「たとえばね」
ユーリ「ごめん、なんかごちゃごちゃしてきた。なに考えてたんだっけ」
僕「うん。ちょっと整理しよう」
ユーリ「うん」
僕「《かかった時間》をすごくすごくすごくすごく短くして、 その間の《位置の変化》を計る。 そして、《位置の変化》を《かかった時間》で割り算する。そうすれば《速度のグラフ》ができる」
ユーリ「そんなのたいへんじゃん」
僕「たいへんだね。 ……じゃ、単純な《位置のグラフ》を数学的に作ることにしよう」
ユーリ「数学的に作る?」
僕「つまり、《位置のグラフ》を数式で作って、その《速度のグラフ》がどうなるかを実際に計算してみようということ」
ユーリ「うわ、めちゃくちゃめんどそう!」
僕「でも、実際に計算してみると微分を実感できるよ。 そうしたら、ユーリがいつも数学で競っている友達に自慢できるんじゃないかなあ……」
ユーリ「え、そっか……」
僕「まあ、確かに多少めんどうだけど、どうする?」
ユーリ「やってみる! 《位置のグラフ》から《速度のグラフ》を作ればいーんだよね?」
僕「うん、そうだよ」
ユーリ「そんで? どーゆー《位置のグラフ》?」
僕「とても簡単だけど、直線じゃないグラフでやってみよう。こういうもの」
これから考える《位置のグラフ》
直線上を動く動点が、時刻 $t$ のときに次のような位置 $p$ にあるとする。
$$ p = t^2 $$
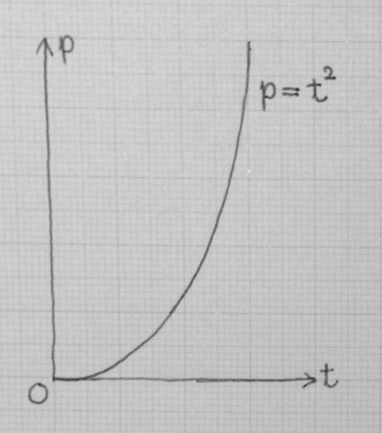
ユーリ「ふーん。《位置のグラフ》を見るとぐいーんと速くなってる感じがするけど……」
僕「ある時刻 $t$ で、動点は $p$ という位置にいる。 そしてその位置 $p$ というのは時刻を使って $p = t^2$ と表せるとする。 たとえばそういう状況を考えてみよう、ということだよ」
ユーリ「うん」
僕「試しに少し計算してみよう。たとえば、時刻が $1$ のとき、位置 $p$ はどうなる?」
ユーリ「えーと。 $t = 1$ のときだから、 $p = 1$ でいーの?」
僕「それでいいよ。 $t = 1$ のとき、 $p = t^2 = 1^2 = 1$ という計算をしたんだよね」
ユーリ「うん。時刻を $2$ 乗すればいいだけだからカンタン」
僕「簡単になるように数式を使って《位置のグラフ》を作ったからね。 それじゃ、時刻が $2$ のとき、位置 $p$ はどうなる?」
ユーリ「$2$ 乗するんだから、 $4$」
僕「そうそう。 $t = 2$ のとき、 $p = t^2 = 2^2 = 4$ になる」
ユーリ「カンタンカンタン」
僕「これで、時刻が $1$ から $2$ に変化したときの《位置の変化》がわかったから、速度を計算してみよう。 速度の定義……」
ユーリ「速度の定義にあてはめるんでしょ? ユーリがやる!」
時刻が $1$ から $2$ に変化したときの速度を求める(かかった時間は $1$)
$$ \begin{align*} \REMTEXT{速度} &= \frac{\REMTEXT{位置の変化}}{\REMTEXT{かかった時間}} \\ &= \frac{\REMTEXT{変化後の位置} - \REMTEXT{変化前の位置}}{\REMTEXT{変化後の時刻} - \REMTEXT{変化前の時刻}} \\ &= \frac{2^2 - 1^2}{2 - 1} \\ &= \frac{4 - 1}{2 - 1} \\ &= \frac{3}{1} \\ &= 3 \\ \end{align*} $$
ユーリ「だから……速度は $3$ でしょ?」
僕「そうそう。その通り。時刻が $1$ から $2$ に変化したときの速度は $3$ になる。 ここで《かかった時間》は $2-1 = 1$ だ。それでね、ここから《かかった時間》を短くして計算してみる」
ユーリ「どんくらい短くするの?」
僕「たとえば、十分の一にしてみよう。つまり時刻が $1$ から $1.1$ に変化したときの速度を求めるということ」
ユーリ「カンタンだよ。だって、おんなじ計算すればいいんでしょ?」
僕「そうだね」
ユーリ「計算、しよー!」
時刻が $1$ から $1.1$ に変化したときの速度を求める(かかった時間は $0.1$)
$$ \begin{align*} \REMTEXT{速度} &= \frac{\REMTEXT{位置の変化}}{\REMTEXT{かかった時間}} \\ &= \frac{\REMTEXT{変化後の位置} - \REMTEXT{変化前の位置}}{\REMTEXT{変化後の時刻} - \REMTEXT{変化前の時刻}} \\ &= \frac{1.1^2 - 1^2}{1.1 - 1} \\ &= \frac{1.21 - 1}{1.1 - 1} \\ &= \frac{0.21}{0.1} \\ &= 2.1 \\ \end{align*} $$
僕「できたね」
ユーリ「今度は $2.1$ になった……あれ? さっきは $3$ だったよ。速度が変わったってこと?」
僕「《かかった時間》を変えれば、速度は変わるよ。 時刻が $1$ から $2$ までの速度は大きい($3$)けど、 $1$ から $1.1$ までの速度はそれほどじゃない($2.1$)というわけだね」
ユーリ「……」
僕「この動点は、時間が経てば経つほど速度が大きくなっていくわけだから、 《かかった時間》を小さくすれば、速度は小さくなる」
ユーリ「……じゃ、やっぱり、《かかった時間》を小さくしたらゼロになるんじゃないの?」
僕「それを確かめるために、いまコツコツと計算しているんだから、もうちょっと先に進もう」
ユーリ「むー、そっか」
僕「では次に、《かかった時間》をさらに十分の一にして速度を計算しよう」
ユーリ「$1$ から $1.01$ だね!」
時刻が $1$ から $1.01$ に変化したときの速度を求める(かかった時間は $0.01$)
$$ \begin{align*} \REMTEXT{速度} &= \frac{\REMTEXT{位置の変化}}{\REMTEXT{かかった時間}} \\ &= \frac{\REMTEXT{変化後の位置} - \REMTEXT{変化前の位置}}{\REMTEXT{変化後の時刻} - \REMTEXT{変化前の時刻}} \\ &= \frac{1.01^2 - 1^2}{1.01 - 1} \\ &= \frac{1.0201 - 1}{1.01 - 1} \\ &= \frac{0.0201}{0.01} \\ &= 2.01 \\ \end{align*} $$
僕「計算ミスしてない? 桁には特に注意だよ」
ユーリ「だいじょーぶだって。今度は速度は $2.01$ になった。やっぱり小さくなったけど……でも、《かかった時間》ほどは小さくなってない……」
僕「お、いい観察」
ユーリ「ねーハカセ」
僕「どこに博士が」
ユーリ「ユーリ、思ったんだけど」
僕「ん?」
ユーリ「ユーリ、思ったんだけど、かかった時間を $0.001$ にしたら、速度は $2.001$ になるんじゃないかにゃ?」
僕「どうしてそう思ったのかにゃ?」
ユーリ「まねするなー……! あのね、《かかった時間》を $1 \to 0.1 \to 0.01$ って変えたとき、 速度は $3 \to 2.1 \to 2.01$ ってなったから。規則的じゃん? 特に $2.1$ と $2.01$ のとこ」
$$ \begin{array}{c|llllll} \hline \REMTEXT{《かかった時間》} & 1 & 0.1 & 0.01 & \cdots \\ \hline \REMTEXT{《速度》} & 3 & 2.1 & 2.01 & \cdots \\ \hline \end{array} $$僕「ん? ユーリの目には $3$ は規則的に見えない?」
ユーリ「へ? お兄ちゃんには規則的に見えるの?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 420本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2013年8月30日)
この記事は『数学ガールの秘密ノート/微分を追いかけて』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!