![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
テトラちゃんと僕は図書室で数学に取り組んでいる。 絶対値を使ったグラフについて話し合っていると、 急にテトラちゃんが大声を出した。
テトラ「先輩! あたし、すごい問題おもいついてしまいましたっ!」
僕「問題?」
テトラ「これです!」
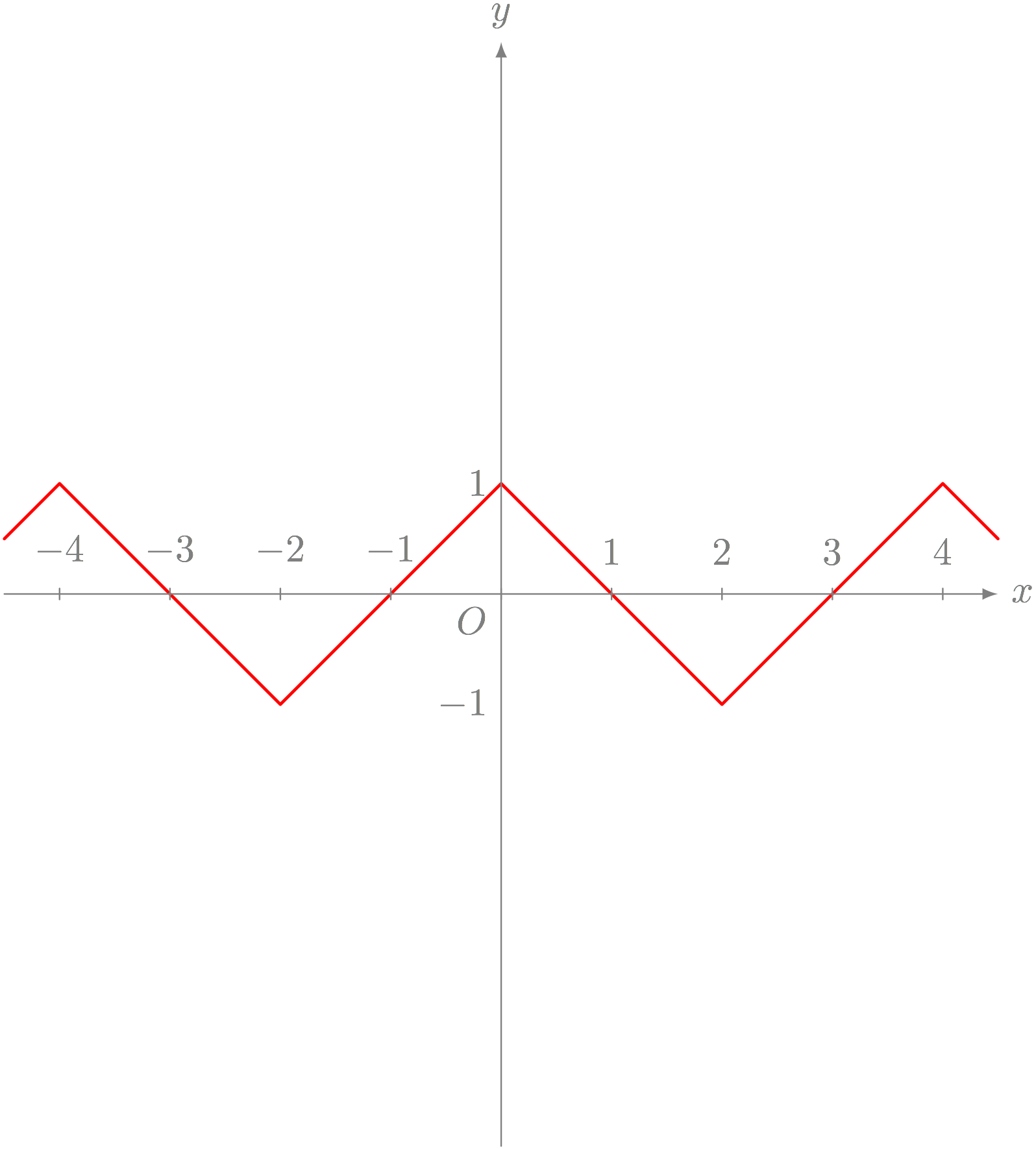
問題X
以下のグラフを表す方程式を答えよ。
僕「おっと!」
テトラ「このジグザグはどんな式で表せるんでしょうか?!」
僕「……このグラフ、ずっと続いているってことだよね?」
テトラ「はい、そうですっ! 無限のかなたから、無限のかなたまで!」
テトラちゃんは、大きな目をキラキラさせて僕を見つめている。
僕「なるほどねえ……テトラちゃんはどんなふうに考える?」
テトラ「はい。先ほど先輩は《$x$ の範囲を工夫して場合分け》なさっていましたよね。 あれと同じように考えればいいんじゃないかと思います(第81回参照)」
僕「うんうん」
テトラ「つまり、山と谷に分ければすぐにできそうですっ!」
山と谷に分ける
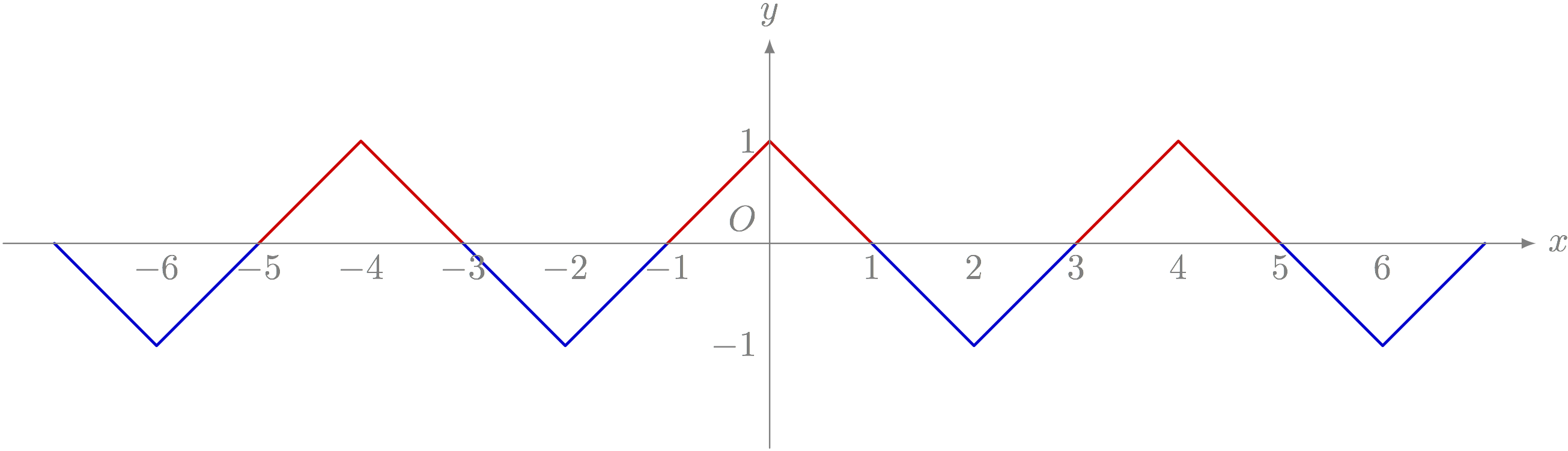
僕「うん、それは自然な発想だよね。ところで $x$ の範囲と、範囲ごとの方程式は書ける?」
テトラ「まず、真ん中の山は先ほど求めました。 $-1 < x < 1$ の範囲で $y = -\ABS{x} + 1$ です」
僕「そうだね」
テトラ「それから、右の山は $3 < x < 5$ の範囲で……あ、 $y = -\ABS{x} + 1$ じゃない……」
僕「うん、右に $4$ だけ平行移動しなきゃいけないね」
テトラ「ということは、 $x$ を $4$ 増やすから $y = -\ABS{x + 4} + 1$ ですね」
僕「違うよ、逆なんだ。それ、すごく間違いやすいところ。 《グラフを右に $4$ 動かす》というときは $x$ を $x - 4$ に変えた方程式にしなくちゃいけないんだよ。 つまり、 $y = -\ABS{x} + 1$ を $y = -\ABS{x - 4} + 1$ にするんだね」
テトラちゃんはそこでしばらく考え込んだ。
テトラ「そうですね……わかりました。 《$x$ が $-1$ から $1$ まで動くとき》と同じ形を《$x$ が $3$ から $5$ まで動くとき》に描く……ということは、 確かに $x$ を $x - 4$ にしないとまずいですね」
僕「あわてると、それよく間違えるんだよ」
テトラ「えっと、ですから、 $3 < x < 5$ の範囲で $y = -\ABS{x - 4} + 1$ になります」
僕「そうだね。左の山は?」
テトラ「左の山は、 $-5 < x < -3$ の範囲で $y = -\ABS{x + 4} + 1$ です。こっちは逆に $x + 4$ にするんですね」
僕「うん、いいね」
テトラ「右の谷は……これは右に $2$ 動かしますから、 $1 \leqq x \leqq 3$ の範囲で $y = \ABS{x - 2} - 1$ です。 左の谷は、 $-3 \leqq x \leqq -1$ の範囲で $y = \ABS{x + 2} - 1$ です……」
僕「そのくらい調べたら、規則性を見つけて、一般的に表現できそうだね。 何しろ無数の山と谷を相手にしなくちゃいけないから、一般的に表現しないとまずい」
テトラ「はい……整理します。まず、山の方から」
山の整理
$$ y = \left\{\begin{array}{llll} -\ABS{x + 4} + 1 & (-5 < x < -3) \\ -\ABS{x} + 1 & (-1 < x < 1) \\ -\ABS{x - 4} + 1 & (3 < x < 5) \\ \end{array}\right. $$
僕「さあ、この三個から規則性を見つけられる?」
テトラ「……はい、できそうです。左右に $4$ ずつ動かせばいいので、 $4$ の倍数を作ればいいんですね?」
山を一般的に表す
$$ y = -\ABS{x - 4n} + 1 \qquad (4n - 1 < x < 4n + 1) $$
$n$ は整数($\ldots, -3,-2,-1,0,1,2,3, \ldots$)
僕「いいねえ。 $n = -1, 0, 1$ で検算すると……うん、あってる」
テトラ「同じように谷も整理します」
谷の整理
$$ y = \left\{\begin{array}{llll} \ABS{x + 6} - 1 & (-7 \leqq x \leqq -5) \\ \ABS{x + 2} - 1 & (-3 \leqq x \leqq -1) \\ \ABS{x - 2} - 1 & (1 \leqq x \leqq 3) \\ \ABS{x - 6} - 1 & (5 \leqq x \leqq 7) \\ \end{array}\right. $$
僕「こっちもすぐ一般的に書けそうだ」
テトラ「はい!」
谷を一般的に表す
$$ y = \ABS{x - 4n - 2} - 1 \qquad (4n + 1 \leqq x \leqq 4n + 3) $$
$n$ は整数($\ldots, -3,-2,-1,0,1,2,3, \ldots$)
僕「これで完成だね」
テトラ「そうですね……」
テトラちゃんの解答X
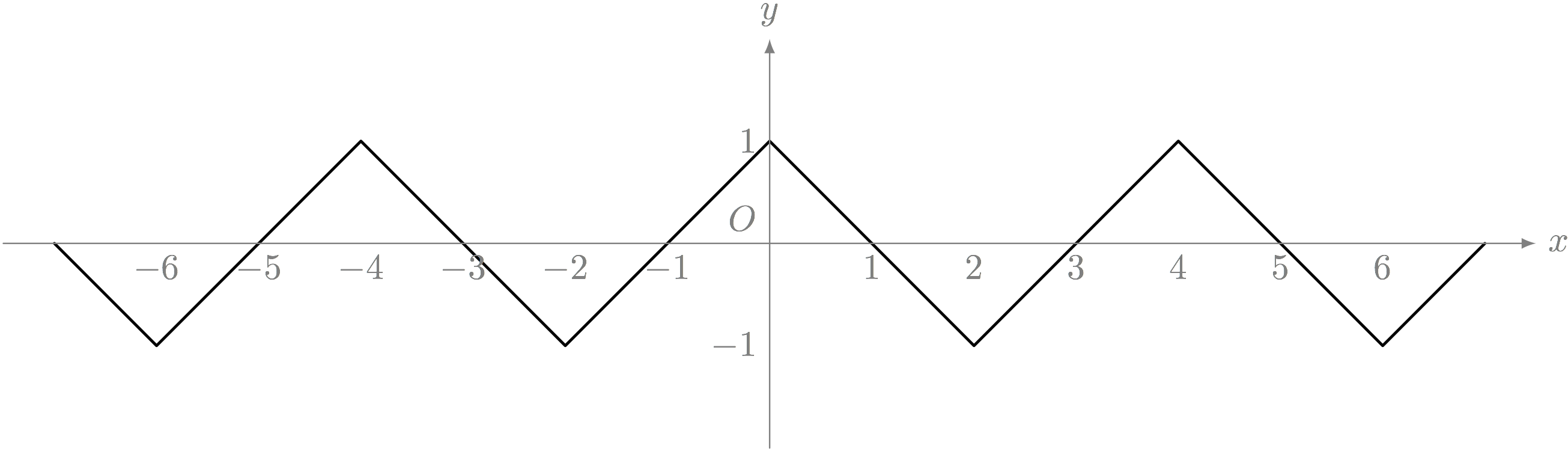
$$ y = \left\{\begin{array}{llll} -\ABS{x - 4n} + 1 & (4n - 1 < x < 4n + 1) \\ \ABS{x - 4n - 2} - 1 & (4n + 1 \leqq x \leqq 4n + 3) \\ \end{array}\right. $$
$n$ は整数($\ldots, -3,-2,-1,0,1,2,3, \ldots$)
テトラ「すぐにできそう!って言っちゃったんですが、 思った以上に大変でした……」
僕「そうだね。こういう場合分けは神経使うし」
テトラ「先輩はこの問題、どのように考えますか?」
僕「テトラちゃんは山と谷に分けて考えたけど、 僕はポリアの問いかけ《似てるものを知らないか》が思い浮かんだなあ」
テトラ「似ているもの……ですか」
僕「うん、このグラフを見ていると最初に思ったのは $y = \cos x$ と似ているなあということ」
$y = \cos x$ のグラフ
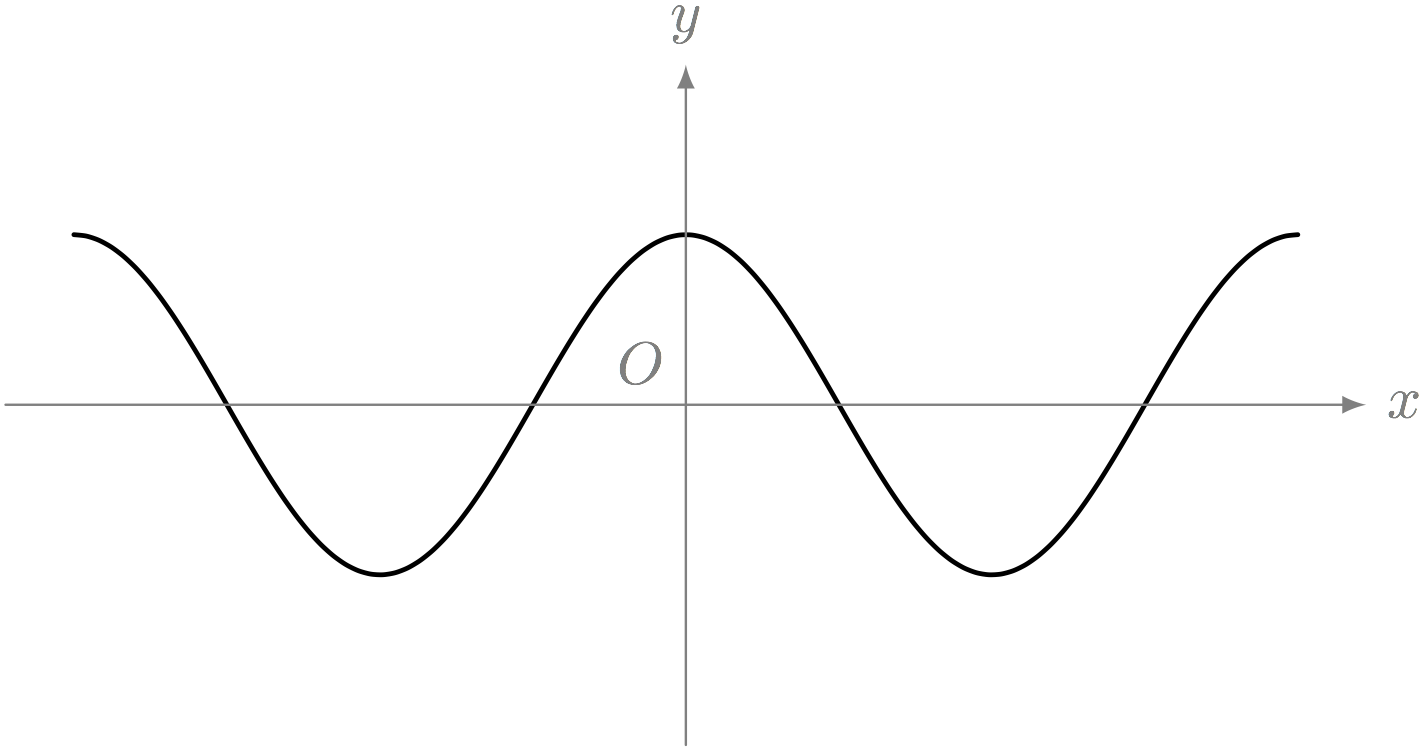
テトラ「なるほどです!あとはこれをまっすぐにすればいいんですね!」
僕「でも、このサインカーブをまっすぐにするのは思いつかなかった。 それから思ったのは、どうしてこの問題Xのグラフが $y = \cos x$ のグラフと似ているかというと、 《周期性》があるからなんだね。つまり、 $x$ が変化したときに $y$ は周期的に同じ値を取る」
テトラ「そうですね」
僕「それで僕が思いついたのは $(-1)^n$ なんだ」
テトラ「$-1$ の $n$ 乗……」
僕「うん。 $(-1)^n$ で、 $n$ を $0,1,2,3,\ldots$ と変化させると、 $n$ が偶数のときは $(-1)^n = 1$ で、 $n$ が奇数のときは $(-1)^n = -1$ になる」
$$ \begin{array}{c|ccccccccccccccccc} n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & \cdots \\ \hline (-1)^n & 1 & -1& 1 & -1& 1 & -1& 1 & \cdots \\ \end{array} $$
テトラ「確かにそうですが……」
僕「だから、 $(-1)^n$ は周期的に同じ値を取る」
テトラ「で、でも先輩、 $(-1)^n$ の $n$ は整数ですよね……」
僕「そうだね。グラフを描くときは、 $x$ は整数だけじゃなくて実数全体を動いてしまう。 だから、こう考えたんだ。《実数から整数を得る関数》を利用すればいいなって」
テトラ「実数から整数を得る関数……といいますと?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 420本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2014年7月11日)