![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/ビットとバイナリー』として書籍化されています。
登場人物紹介
僕:数学が好きな高校男子。
ユーリ:僕のいとこの中学女子。僕のことを《お兄ちゃん》と呼ぶ。
ユーリ「あけおめー」
僕「おめー」
ユーリ「ことよろー」
僕「よろー」
ユーリ「ねー、お兄ちゃん知ってた? $2015$ って、 $2$ 進法で書くと左右対称なんだって」
僕「へえ、そうなんだ」
ユーリ「えーっとね、 $2015$ を $2$ 進法で書くと $11111011111$ なんだよー」
$2015$ を $2$ 進法で書くと左右対称になる
$$ \begin{array}{cc} \REMTEXT{$10$進法} & \REMTEXT{$2$進法} \\ \hline 2015 & 11111011111 \\ \end{array} $$
僕「ユーリ、そんなのよく気付いたなあ」
ユーリ「ネットで話題になってた」
僕「そうなんだ」
ユーリ「それからね、平成 $27$ 年の $27$ も $2$ 進法で書くと左右対称になるんだよ。 $11011$ だって!」
$27$ を $2$ 進法で書くと左右対称になる
$$ \begin{array}{cc} \REMTEXT{$10$進法} & \REMTEXT{$2$進法} \\ \hline 27 & 11011 \\ \end{array} $$
僕「おもしろいな……ユーリ、それメモしてたの?」
ユーリ「そーだよ。お兄ちゃんに教えてあげよーと思って」
僕「そりゃどうも」
ユーリ「こないだお兄ちゃんから $2$ 進法教えてもらってから、 ちょっと興味あるの」
僕「$2$ 進法の話なんてしたっけ?」
ユーリ「したじゃん。ほらほら《数当てマジック》のとき(『数学ガールの秘密ノート/整数で遊ぼう』参照)」
僕「なるほど。 $2$ 進法は好きだよ。 $2$ 進法がらみでは、いろんな数学者が出てくるけど、ライプニッツの話が特に好きだな」
ユーリ「誰それ」
僕「がく。ライプニッツは有名な数学者だよ。 ニュートンと並んで微分を考えた人でもある」
ユーリ「ふーん」
僕「ライプニッツはね、 $10$ 進法で数列を書くよりも $2$ 進法で書いた方が、 パターンを見つけやすくなるっていってる」
ユーリ「パターン?」
僕「うん。数列が持っているパターンが見つけやすくなるということは、 数列が持っている性質を見つけやすくなるってことだね」
ユーリ「そーなんだ」
僕「さっきユーリがいってた《左右対称》っていうのもパターンの一種といえるかも」
ユーリ「どーして、 $2$ 進法だとパターンが見つけやすいの?」
僕「どうして見つけやすいか……そうだなあ。 $2$ 進法で使われている数字は $0$ と $1$ しかないからかもね。 $10$ 進法だと $0$ から $9$ まで使うから、 数の並びがあったときにどれとどれが同じかわかりにくい。 でも $2$ 進法だと $0$ と $1$ だけだから、《$0$ が連続している》や 《いつも右端に $1$ が来る》や《左右対称》みたいな性質に気付きやすいのかな」
ユーリ「ふーん……」
ユーリ「ところで、 $2$ 進法って $0$ と $1$ しか使わないの?」
僕「えっ! そうだよ。だって、 $2$ 進法だと、 $2$ になったら繰り上がりが起きるから」
ユーリ「あ、そっか」
僕「ほんとにわかってるのかなあ」
ユーリ「わーってるって」
僕「$0,1,2,3,4,5,\ldots$ を、 $2$ 進法で数えられる?」
ユーリ「えーと、たぶんね。最初 $0$ でしょ。次が $1$ で、そん次が $10$(イチゼロ)」
僕「そら、そこで繰り上がりが起きてるよね。 $1$ に $1$ 足したら、 $2$ 進法だと $10$ になる。繰り上がりして $2$ 桁の数になった」
ユーリ「そだね。ユーリ、表を作れるよ」
$10$ 進法と $2$ 進法の対応表 $$ \begin{array}{rr} \REMTEXT{$10$進法} & \REMTEXT{$2$進法} \\ \hline 0 & 0 \\ 1 & 1 \\ 2 & 10 \\ 3 & 11 \\ 4 & 100 \\ 5 & 101 \\ 6 & 110 \\ 7 & 111 \\ 8 & 1000 \\ 9 & 1001 \\ 10 & 1010 \\ 11 & 1011 \\ 12 & 1100 \\ 13 & 1101 \\ 14 & 1110 \\ 15 & 1111 \\ \vdots & \vdots \\ \end{array} $$
ユーリ「ね? ちゃんとわかってるでしょ?」
僕「そうだね。ライプニッツの言う通り、 この表だけでもパターンがいくつか見えるよね」
ユーリ「縦読みするんでしょ? 一番右端の数は $0,1,0,1,0,1,\ldots$ になってる」
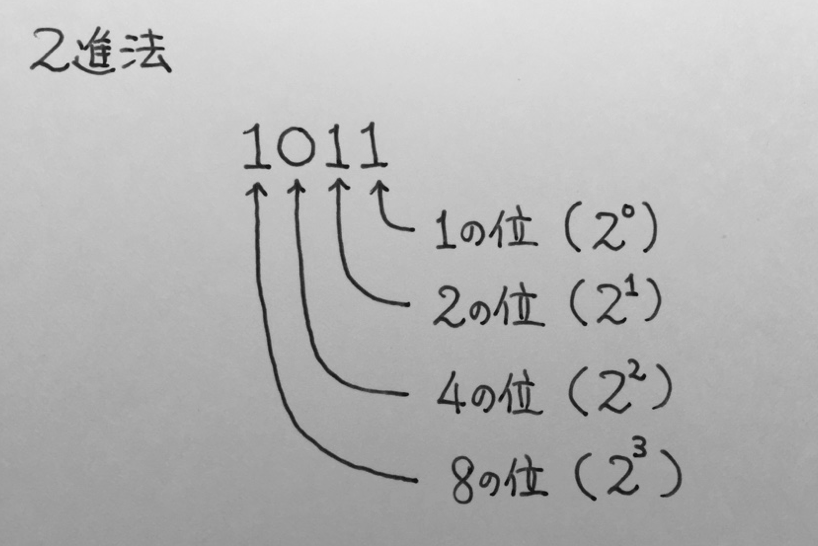
僕「うん。一番右端の数は、 $2$ 進法の《$1$ の位(くらい)》だね。 この数が $0$ ならば偶数だし、この数が $1$ ならば奇数だ」
ユーリ「それから、縦読みすると、右から二番目の数は $0,0$ と $1,1$ がかわりばんこ」
僕「右から二番目の数は、 $2$ 進法の《$2$ の位》になるね。 $10$ 進法だと《$1$ の位》《$10$ の位》《$100$ の位》《$1000$ の位》……になるけど、 $2$ 進法だと《$1$ の位》《$2$ の位》《$4$ の位》《$8$ の位》……になるんだよ」
ユーリ「ふんふん」
$10$ 進法と $2$ 進法の位(くらい)

僕「じゃ、ここでクイズを出すよ」
ユーリ「なになに?」
僕「$10$ 進法で書いたときに $19$ になる数を、 $2$ 進法で書いたらどうなる?」
ユーリ「わかんない。覚えてないもん」
僕「がく。お兄ちゃんだって覚えていないよ。どうなるかを考えてほしいんだけど」
ユーリ「えー……あ、そっか。さっき $15$ までの表を作ったから、 そこから始めればいっか。 $15$ が $1111$ で、 $16$ が $10000$ で、 $17$ が $10001$ で、 $18$ が $10010$ だから、 $19$ は $10011$ だ!」
僕「はい正解。 $10$ 進法で $19$ と表す数は、 $2$ 進法では $10011$ と表せるね」
$10$ 進法と $2$ 進法(続き) $$ \begin{array}{rr} \REMTEXT{$10$進法} & \REMTEXT{$2$進法} \\ \hline \vdots & \vdots \\ 14 & 1110 \\ 15 & 1111 \\ 16 & 10000 \\ 17 & 10001 \\ 18 & 10010 \\ 19 & 10011 \\ \vdots & \vdots \\ \end{array} $$
ユーリ「かんたんだよ」
僕「じゃ、 $39$ を $2$ 進法で書いたらどうなる?」
ユーリ「おんなじじゃん! $20$ のときは $10100$ ……みたいに書いてけばいーよね! めんどいからやりたくないけど」
僕「うん、そういうと思ったよ。ユーリがさっきやったみたいに、 $1$ ずつ増やしていく方法は悪くない。でも、大きな数を $2$ 進法で表そうとしたときには、 すごくめんどうなことになってしまうよね」
ユーリ「そだね……でも、他に方法あるの?」
僕「それが問題になる」
問題1
$10$ 進法で書くと $39$ になる数を、 $2$ 進法で書くとどうなるか。
ユーリ「どーすんのかにゃあ……」
僕「たとえば、こんなやりかたがある。 $10$ 進法で書かれた数を読むときに $1,10,100,1000,10000,\ldots$ と唱えるよね」
ユーリ「うん、やるやる。いち、じゅう、ひゃく、せん、まん」
僕「$2$ 進法でもそれと同じようにやってみる。 ただし、 $1,2,4,8,16,32,\ldots$ と唱える」
ユーリ「$2$ 進法だから $2$ 倍に?」
僕「そうだね。いま調べたいのは $39$ の書き方だから、 $39$ に近くなるまではその方法を使う。 $\underbrace{1,2,4,8,16,32}_{\REMTEXT{$6$個}}$だから、$2$進法で$100000$という$6$桁の数は$32$になる。 あとはこれに $10$ 進法の $7$ 、つまり $2$ 進法の $111$ を足せばいい。 $2$ 進法で $100000 + 111$ を計算すれば $100111$ だね。これが $39$ に相当する」
ユーリ「$7$ ってどっから来たの?」
僕「すでにわかった $32$ から、いま表したい数 $39$ まで進むのにあと $7$ ってこと。 つまり $39 - 32 = 7$ だね」
ユーリ「あ、そっか、わかった」
解答1
$10$ 進法で書くと $39$ になる数を、 $2$ 進法で書くと $100111$ になる。
僕「いまのは、自分が $2$ 進法で表したい数の近くまでは、 倍々で進んでいくという方法だね。これだと $1$ ずつ増やすよりずっと楽だ」
ユーリ「でもさー、もっと大きな数だとやっぱりめんどくなるよ」
僕「うん、そろそろ一般的に《$10$ 進数を $2$ 進数で表す方法》を考えた方がよさそうだ。 そもそも、 $10$ 進法で $39$ になる数が、 $2$ 進法で $100111$ と書けるというのは、 どういうことかを考えてみよう。これは、こういうことなんだ」
$$ \begin{align*} 39 & = 32 + 4 + 2 + 1 \\ & = 2^5 + 2^2 + 2^1 + 2^0 \\ & = \BIGUL{1}\cdot2^5 + \BIGUL{0}\cdot2^4 + \BIGUL{0}\cdot2^3 + \BIGUL{1}\cdot2^2 + \BIGUL{1}\cdot2^1 + \BIGUL{1}\cdot2^0 \\ \end{align*} $$
ユーリ「?」
僕「つまり、 $39$ という数を、 $1,2,4,8,16,32,\ldots$ という $2$ の冪乗(べきじょう)の数の《和》の形で 表しているということ」
ユーリ「あー、そーだった。そんな話してたねー」
僕「$39$ という数は、 $32, 4, 2, 1$ という $2$ の冪乗の和に書ける。 これはそれぞれ $2^5, 2^2, 2^1, 2^0$ という形。 途中の $2^4$ と $2^3$ は飛ばしている。これを入れちゃうと $39$ は作れないから。 どの数を使って、どの数を飛ばすかは、 $1$ を掛けるか $0$ を掛けるかで表す。 $2$ 進法では $2$ の冪乗を使うことになっているから、 あとは、その $1$ と $0$ の並びさえわかればいいってことになる。 このときの $1$ と $0$ の並びが《$2$ 進法で書かれた数》すなわち《$2$ 進数》になる」
$$ 39 = \BIGUL{1}\cdot2^5 + \BIGUL{0}\cdot2^4 + \BIGUL{0}\cdot2^3 + \BIGUL{1}\cdot2^2 + \BIGUL{1}\cdot2^1 + \BIGUL{1}\cdot2^0 $$
下線部の $1$ と $0$ の並びは $100111$ になる。
ユーリ「ふんふん」
僕「この《$2$ の冪乗のうち、どれを足してどれを足さないか》を表したものが $2$ 進数だとわかっていれば、 $10$ 進数を $2$ 進数に変換する方法も見つけることができるんだよ」
ユーリ「へー!」
僕「ひとことでいえば《繰り返して $2$ で割って余りを調べていく》というやり方なんだ」
ユーリ「どゆこと?」
僕「$39$ の例でいおう。 $39$ を $2$ で割ったときの余りは?」
ユーリ「$39 \div 2$ は $19$ で余りは $1$」
僕「そうだね。そしてこの余り $1$ は、 $39$ を $2$ 進法で表したときの一番右に来る数になる。《$1$ の位》」
ユーリ「なんで?」
僕「なぜだと思う?」
ユーリ「……あ! そりゃそーじゃん。 $2$ 進数だと、偶数は $0$ で終わるし、奇数は $1$ で終わるもん。 $2$ で割って余り $1$ っていうのは要するに奇数ってことだし」
僕「そうだね。さっきの数式を思い出してもわかる。《$1$ の位》はちょうど $2$ で割った余りに相当する」
$$ \begin{align*} 39 & = \BIGUL{1}\cdot2^5 + \BIGUL{0}\cdot2^4 + \BIGUL{0}\cdot2^3 + \BIGUL{1}\cdot2^2 + \BIGUL{1}\cdot2^1 + \BIGUL{1}\cdot2^0 \\ & = \underbrace{2\left( \BIGUL{1}\cdot2^4 + \BIGUL{0}\cdot2^3 + \BIGUL{0}\cdot2^2 + \BIGUL{1}\cdot2^1 + \BIGUL{1}\cdot2^0 \right)}_{\REMTEXT{$2$でくくった}} + \underbrace{\BIGUL{1}\cdot2^0}_{\REMTEXT{$2$で割ったあまり}} \\ \end{align*} $$
ユーリ「ほほー。そっか $2^0$ のところがちょうど余りになるんだ」
僕「これで、《$1$ の位》はわかったね。 そして、いま《$2$ でくくった》と書いたところをよく見ると、 ここも同じように考えればいいってことがわかる。 つまり、さっき《$39$ を $2$ で割ったときの商 $19$》を、 さらに $2$ で割って余りを求めるということ。これで《$2$ の位》がわかる」
ユーリ「ははーん、さっきお兄ちゃんが言った 《繰り返して $2$ で割って余りを調べていく》ってそーゆーこと?」
僕「実際に $39$ でやってみよう。こんなふうになる」
$39$ を $2$ 進法で表す

僕「これで、余りのところを順番に見ていくと $1,1,1,0,0,1$ だね。 これは下の位から見ていることになるから、逆転させて $100111$ になる。 $39$ を $2$ 進法で書くと、 $100111$ になるということだね」
ユーリ「あれ? これやったことある。 ほら、お兄ちゃんが描いてくれた変なワニが出てきたやつ!」
僕「そうそう、そうだったね。 この方法を使えば、自分の手で $2015$ を $2$ 進法で書いたらどうなるかを調べられるよ」
僕「いまは $39$ を例に使って $2$ 進数の話をしたけど、 シグマ $\sum$ を使えば、もっと一般的に書くことができるよ」
ユーリ「キター! お兄ちゃん得意の《一般的に書く》だ!」
僕「何興奮してんの」
ユーリ「お兄ちゃん、一般化するの好きだよね」
僕「まあね。さっきの $39$ の式をじっと見れば、一般的にどう書けばいいかはすぐわかるよ」
ユーリ「じー」
$$ \BIGUL{1}\cdot2^5 + \BIGUL{0}\cdot2^4 + \BIGUL{0}\cdot2^3 + \BIGUL{1}\cdot2^2 + \BIGUL{1}\cdot2^1 + \BIGUL{1}\cdot2^0 $$
僕「まずは、 $0$ と $1$ の部分を $a_k$ という文字を使って書いてみよう。 $a_k$ という文字は、《$2^k$ の位》の数字が何になるかを表しているもの、ということに決めて」
$$ a_5\cdot2^5 + a_4\cdot2^4 + a_3\cdot2^3 + a_2\cdot2^2 + a_1\cdot2^1 + a_0\cdot2^0 $$
ユーリ「ほほー……ねー、この $a_5$ とか、 $a_4$ って、 $0$ か $1$ かのどっちかだよね?」
僕「そうそう。それでと。いまは $6$ 桁の $2$ 進数固定になっているから、 $n$ 桁の $2$ 進数に変えてみよう。 途中にテンテン($\cdots$)を入れる」
$$ {a_{n-1}}\cdot2^{n-1} + {a_{n-2}}\cdot2^{n-2} + {a_{n-3}}\cdot2^{n-3} + \cdots + {a_2}\cdot2^2 + {a_1}\cdot2^1 + {a_0}\cdot2^0 $$
ユーリ「何で $n-1$ なの? ……わかった! $0$ から始めたからだね!」
僕「そうだね。《$n$ 桁の $2$ 進数》だとしたら、最上位は《$2^{n-1}$ の位》になる。 こういうのはすごくまちがいやすいところだね」
ユーリ「ねー、《$n+1$ 桁の $2$ 進数》を表すってことにすれば $a_n$ から $a_0$ まででちょーどいーんじゃないの?」
僕「うん、そういう表し方をしてもいいよ。それから、《$2^k$ の位》の数字を $a_{k+1}$ にするというやり方もある。 これは約束ごとなんだから、書く人が自由に決めていい。何を表しているかをはっきり言えば」
ユーリ「約束ごと……ね」
僕「さて、こんなふうにテンテンを使った足し算の形にうまく書けたら、シグマまではもう一息。 何しろシグマは足し算なんだから」
$$ \begin{align*} & {a_{n-1}}\cdot2^{n-1} + {a_{n-2}}\cdot2^{n-2} + {a_{n-3}}\cdot2^{n-3} + \cdots + {a_2}\cdot2^2 + {a_1}\cdot2^1 + {a_0}\cdot2^0 \\ &= \sum_{k=0}^{n-1} a_{k}2^{k} \\ \end{align*} $$
ユーリ「うわ、すごくややこし……くもないか」
僕「足し算を置き換えているだけだから、ぜんぜん、ややこしくないよね。 これで、 $2$ 進法で表した $0$ 以上の整数を、シグマで表現することができた」
$0$ 以上の整数 $N$ が、 $2$ 進法で、 $$ a_{n-1}a_{n-2}\ldots a_{2}a_{1}a_{0} $$ と表記できたとする。 ここで $a_k$ は《$2^k$ の位》の数字を表しているものとする。 $a_k$ は $0$ または $1$ である。
このとき、 $$ N = \sum_{k=0}^{n-1} a_{k}2^{k} $$ が成り立つ。
僕「これで、 $2$ 進数を数式で書くことができたね」
ユーリ「お兄ちゃんってほんとに、数式好きなんだね」
僕「そうだね。 そうだ! ユーリがいってた《左右対称な $2$ 進数》もやってみようよ」
ユーリ「何をやるの?」
僕「数式……シグマを使って表してみるんだよ」
問題2
$2$ 進法で書いたときに《左右対称》になる数をシグマを使った数式で表せ。
ユーリ「どゆ意味?」
僕「さっきは $\SUM_{k=0}^{n-1} a_k2^k$ という数式で、 $2$ 進数を書くことができたよね」
ユーリ「うん」
僕「どんな $2$ 進数でもこの数式で表現できる。 けれど今度は、左右対称な $2$ 進数に限って表現するような数式を作ろうということ」
ユーリ「左右対称……って、そんなこと数式で書けんの?」
僕「もちろん書けるよ。つまりこれは《言い換え》なんだ」
ユーリ「言い換え?」
僕「そう。さっき、 $2$ 進数はパターンが見やすいという話をしたよね。 $111101111$ や $11011011$ のように数字が並んでいると、パッと見て《あ、左右対称だ》ってわかる」
ユーリ「うん」
僕「それは見て分かるということ。 ではそれを数学の言葉……数式で表現し直してみよう。言い換えてみよう」
ユーリ「ふんふん。左右対称……さっぱりわかんない」
僕「じゃね、まずは数式じゃなくてもいいから自分の言葉で表現してみよう。 $11011011$ のような $2$ 進数は左右対称だよね」
ユーリ「そだね」
僕「なぜ、左右対称っていえるんだろう」
ユーリ「だって、左端から $1,1,0,1$ と並んでいて、右端からも同じく $1,1,0,1$ って並んでるから」
僕「そうだね! 一つずついこう。 《左端が $1$ で右端も $1$》つまり《左端と右端が等しい》」
ユーリ「$2$ 番目もそうだよ。左から $2$ 番目と右から $2$ 番目も等しい」
僕「$1$ 番目、 $2$ 番目、 $3$ 番目……ずっとそうだね。それが《左右対称》ということ」
ユーリ「あたりまえじゃん」
僕「ところで、僕たちはこんなふうにして $2$ 進数を数式で表現できる」
$$ {a_{n-1}}\cdot2^{n-1} + {a_{n-2}}\cdot2^{n-2} + {a_{n-3}}\cdot2^{n-3} + \cdots + {a_2}\cdot2^2 + {a_1}\cdot2^1 + {a_0}\cdot2^0 $$ユーリ「さっきやった」
僕「これで、左端の数字ってなんだろう」
ユーリ「えーっと、 $a_{n-1}$ かにゃ?」
僕「そう。じゃ、右端は?」
ユーリ「$a_0$ でしょ?」
僕「そうだね。ところで、左端の数字と右端の数字が等しいということは」
ユーリ「あっ! $a_{n-1} = a_0$ だ!」
僕「そうなるね。いいぞ!」
ユーリ「でも、こんなイコールをシグマに入れるの?」
僕「ちがうちがう。 $a_{n-1} = a_0$ ということは、 $a_{n-1}$ の代わりに $a_0$ を入れてもいいってことだよね。 だから、両端が等しい数字になった $2$ 進数っていうのはこんな形ってことだよね」
$$ {a_0}\cdot2^{n-1} + \cdots + {a_0}\cdot2^0 $$ユーリ「あ、わかった。もー、いわなくっていい!同じこと繰り返せばいいんだね! こーだ!」
$$ {a_0}\cdot2^{n-1} + {a_1}\cdot2^{n-2} + {a_2}\cdot2^{n-3} + \cdots + {a_2}\cdot2^2 + {a_1}\cdot2^1 + {a_0}\cdot2^0 $$僕「そうだね! これでほとんど正解なんだけど、一点注意が必要になる」
ユーリ「真ん中でしょ? そかそか、 $n$ 桁のちょうど半分まで行くから、 $\frac{n}{2}$ まで……から $1$ 個ずれるから、うわめんどい」
$$ \begin{align*} & {a_0}\cdot2^{n-1} + {a_1}\cdot2^{n-2} + {a_2}\cdot2^{n-3} + \cdots + a_{\frac{n}{2}}\cdot2^{n - \frac{n}{2}} \\ & \quad + a_{\frac{n}{2}}\cdot2^{\frac{n}{2} - 1} + \cdots + {a_2}\cdot2^2 + {a_1}\cdot2^1 + {a_0}\cdot2^0 \\ \end{align*} $$僕「うん、これでほとんど正解。ただしこれは、 $n$ が偶数の場合だよね。 $11$($2$ 桁)や $1001$($4$ 桁)や、 $110011$($6$ 桁)のように、 偶数桁の場合は左右対称で《真ん中》に相当する数がない」
ユーリ「そっか、奇数の場合も考えると……?」
僕「《場合分け》になるね」
解答2
左右対称の $2$ 進数は、以下のように表現できる。
偶数桁($n$ が偶数)の場合:
$$ \begin{align*} & {a_0}\cdot2^{n-1} + {a_1}\cdot2^{n-2} + {a_2}\cdot2^{n-3} + \cdots + a_{\frac{n}{2}-1}\cdot2^{n - \frac{n}{2}} \\ & + a_{\frac{n}{2}-1}\cdot2^{\frac{n}{2} - 1} + \cdots + {a_2}\cdot2^2 + {a_1}\cdot2^1 + {a_0}\cdot2^0 \\ & = \sum_{k=0}^{\frac{n}{2} - 1} a_{k}\left(2^{n-k-1} + 2^k\right) \\ \end{align*} $$
奇数桁($n$ が奇数)の場合:
$$ \begin{align*} & {a_0}\cdot2^{n-1} + {a_1}\cdot2^{n-2} + {a_2}\cdot2^{n-3} + \cdots + a_{\frac{n-1}{2}-1}\cdot2^{n - \frac{n-1}{2}} \\ & \quad + a_{\frac{n-1}{2}}\cdot2^{\frac{n-1}{2}} \\ & \quad \quad + a_{\frac{n-1}{2}-1}\cdot2^{\frac{n-1}{2} - 1} + \cdots + {a_2}\cdot2^2 + {a_1}\cdot2^1 + {a_0}\cdot2^0 \\ & = \sum_{k=0}^{\frac{n-1}{2} - 1} a_{k}\left(2^{n-k-1} + 2^k\right) + a_{\frac{n-1}{2}}2^{\frac{n-1}{2}} \\ \end{align*} $$
ユーリ「うわ……できたけど、すごくめんどい……」
僕「うーん、分数に持ち込んだのが敗因かな」
ユーリ「どゆこと?」
僕「ほら、《$n$ 桁の $2$ 進数》を表現しようとしたから、 $\frac{n}{2}$ や $\frac{n-1}{2}$ というのが出てきちゃったんだ」
ユーリ「だって、しょーがないじゃん」
僕「偶数桁は《$2m$ 桁の $2$ 進数》にして、奇数桁は《$2m+1$ 桁の $2$ 進数》にすれば、 もっとずっとすっきり書ける!」
解答2'
左右対称の $2$ 進数は、以下のように表現できる。
偶数桁($2m$ 桁)の場合:
$$ \begin{align*} & {a_0}\cdot2^{2m-1} + {a_1}\cdot2^{2m-2} + {a_2}\cdot2^{2m-3} + \cdots + {a_{m-1}}\cdot2^{2m - m} \\ & \quad + {a_{m-1}}\cdot2^{m-1} + \cdots + {a_2}\cdot2^2 + {a_1}\cdot2^1 + {a_0}\cdot2^0 \\ &= \sum_{k=0}^{m - 1} a_{k}\left(2^{2m-k-1} + 2^k\right) \\ \end{align*} $$
奇数桁($2m + 1$ 桁)の場合:
$$ \begin{align*} & {a_0}\cdot2^{2m-0} + {a_1}\cdot2^{2m-1} + {a_2}\cdot2^{2m-2} + \cdots + a_{m-1}\cdot2^{2m - (m-1)} \\ & \quad + a_{m}\cdot2^{m} \\ & \quad\quad + a_{m-1}\cdot2^{m - 1} + \cdots + {a_2}\cdot2^2 + {a_1}\cdot2^1 + {a_0}\cdot2^0 \\ &= \sum_{k=0}^{m - 1} a_{k}\left(2^{2m-k} + 2^k\right) + a_{m}2^{m} \\ \end{align*} $$
ユーリ「あ、分数なくなった」
僕「そうだね。この方がずっとすっきりした」
ユーリ「あ! お兄ちゃん、これおかしーよ!」
僕「何が?」
ユーリ「これだとね、たとえば、 $110$ も左右対称になってしまうもん!」
僕「何で? ああっ、そうか。最上位の $0$ か……」
ユーリ「まー、でも $110$ を $0110$ だと思えば、左右対称になってるけど」
僕「うーむ……」
ユーリ「ねーお兄ちゃん」
僕「なに?」
ユーリ「ややこしいよーな、おもしろいよーな、変な感じ」
僕「そう?」
ユーリ「うん。あのね、数式はやっぱり、ややこしいんだけど、 何度も書いているうちに、何だか少し見慣れてきたのかなー。 それから分数がなくなったときは、おーっと思ったし」
僕「うんうん」
ユーリ「でもね、たとえば、この式 $\SUM_{k=0}^{m - 1} a_{k}\left(2^{2m-k} + 2^k\right) + a_{m}2^{m}$ みても《左右対称》って感じがしないの。だから変な感じ」
僕「なるほどね……非対称に見えるのは、 $2^{2m-k} + 2^k$ の部分だけだよね。 本来なら $s = 2m-k, t = k$ と置いて $2^s + 2^t$ のようにするといいんだけどね。 $0 \leqq t < m, s + t = 2m$ の条件を満たす整数 $s,t$ の範囲で和を取ることになる」
ユーリ「ふーん……ところで、 $2$ 進数じゃなくて $1$ 進数ってないの?」
僕「$1$ 進数?」
僕「いや、 $1$ 進数というのは……どうかな。だって繰り上がりできないし」
ユーリ「あのね、こーゆーの。 $1,11,111,1111,11111,\ldots$」
僕「ほう?」
ユーリ「その数の分だけ $1$ を並べちゃうの! これって $1$ 進法っぽくない?」
僕「確かに、$n$を表すのに$\underbrace{111\cdots111}_{\REMTEXT{$n$個}}$という 書き方をすることにすれば、数は表しているな。でも『$1$ 進法』 と呼ぶのは苦しいなあ」
ユーリ「えー、そっかなー。なんで?」
僕「ほら、 $10$ 進法だと、 $10$ を表す数字はないよね。 $0,1,2,3,4,5,6,7,8,9$ の $10$ 種類の数字を使って一つの桁を表している」
ユーリ「うん」
僕「同じように、 $2$ 進法では、 $2$ を表す数字はなくて、 $0,1$ という $2$ 種類の数字を使って一つの桁を表す。 だから、もしも $1$ 進法があるとしたら、 $1$ を表す数字は使えない」
ユーリ「そっか……あっ! だったら $0$ を並べればいいっ!……ちょっと無理があるか」
僕「そうだね。でも、そんなふうに概念を拡張して考えるのは楽しいよね」
ユーリ「$0$ 進法もダメだし……そうだ! 《$-2$ 進法》は? ねーお兄ちゃん! これならできるじゃん?」
僕「マイナス $2$ 進法……えっと、ん? できるのか?」
ユーリ「お兄ちゃんならできるよ、きっと! 問題にしちゃえ!」
問題3
$10$ 進法で書いたときに $0,1,2,3,4,5,6,7,8,9,10$ となる数を、 それぞれ、 $-2$ 進法で表してみよー!
僕「$-2$ 進法って何だろう。 $-2$ になるごとに繰り上がり?」
ユーリ「わけがわかんないね」
僕「いや、ちがうな。そこが本質じゃないんだ」
ユーリ「どこが本質?」
僕「$10$ 進法は、各桁の数字に $10$ の冪乗を掛けて表した。 $1,10,100,1000,10000,\ldots$ という具合に」
ユーリ「ふんふん?」
僕「同じように $2$ 進法は、 $2$ の冪乗を使った。 $1,2,4,8,16,32,\ldots$ だった。これは $2^0,2^1,2^2,2^3,2^4,2^5,\ldots$」
ユーリ「そーだったね。あ!」
僕「そうだ。もしも $-2$ 進法があるとしたら、 《$-2$ の冪乗》を使うんじゃないか? つまり、 $(-2)^0,(-2)^1,(-2)^2,(-2)^3,(-2)^4,(-2)^5,\ldots$ を使う」
ユーリ「おー! ……でも、使う数字は?」
僕「よくわからないけど、 $0$ と $1$ でやってみよう。 うわ!」
ユーリ「どしたの?」
僕「そうか。 $-2$ の冪乗を使うってことは、正と負が入り交じる!」
ユーリ「へ?」
$-2$ 進数で数を表したらどうなるか
$$ \begin{array}{rrr} \REMTEXT{$-2$進数} & \REMTEXT{値を求める式} & & \REMTEXT{$10$進数} \\ \hline 0 & 0\cdot(-2)^0 &= 0 & 0 \\ 1 & 1\cdot(-2)^0 &= 1 & 1 \\ 10 & 1\cdot(-2)^1 + 0\cdot(-2)^0 &= -2 + 0 & -2 \\ 11 & 1\cdot(-2)^1 + 1\cdot(-2)^0 &= -2 + 1 & -1 \\ 100 & 1\cdot(-2)^2 + 0\cdot(-2)^1 + 0\cdot(-2)^0 &= 4 + 0 + 0 & 4 \\ 101 & 1\cdot(-2)^2 + 0\cdot(-2)^1 + 1\cdot(-2)^0 &= 4 + 0 + 1 & 5 \\ 110 & 1\cdot(-2)^2 + 1\cdot(-2)^1 + 0\cdot(-2)^0 &= 4 - 2 + 0 & 2 \\ 111 & 1\cdot(-2)^2 + 1\cdot(-2)^1 + 1\cdot(-2)^0 &= 4 - 2 + 1 & 3 \\ \vdots & \vdots & & \vdots \\ \end{array} $$
ユーリ「うっわ! $0,1,-2,-1,4,5,2,3$ なんて、順番ぐちゃぐちゃ」
僕「いや、わかったぞ。 $0,1$ のあと、 $2$ を作るためには $4-2$ だと考えればいいんだ。 つまり、軽いジャンプがあるんだよ。 《$(-2)^k$ の位》の数字を $a_k$ としたとき、 この一般式をじっと見て考えればわかる」
$-2$ 進数
$$ a_{n-1}(-2)^{n-1} + \cdots + a_3(-2)^3 + a_2(-2)^2 + a_1(-2)^1 + a_0(-2)^0 $$
ユーリ「この式見てわかんの……?」
僕「少し頭をひねらないと難しいかな……いや、できるできる!」
$-2$ 進数で数を表したらどうなるか
$$ \begin{array}{rrl} \REMTEXT{$-2$進数} & \REMTEXT{$10$進数} & \REMTEXT{メモ} \\ \hline 0 & 0 & \\ 1 & 1 & \\ 110 & 2 & \REMTEXT{$(-2)^2 = 4$に、負数$(-2)^1 = -2$を加える} \\ 111 & 3 & \REMTEXT{上に$1$加える} \\ 100 & 4 & \REMTEXT{$(-2)^2 = 4$} \\ 101 & 5 & \REMTEXT{上に$1$加える} \\ 11010 & 6 & \REMTEXT{$(-2)^4 = 16$に、負数$(-2)^3 = -8$と$(-2)^1 = -2$を加える} \\ 11011 & 7 & \REMTEXT{上に$1$加える} \\ \vdots & \vdots & \vdots \\ \end{array} $$
ユーリ「あれ……お兄ちゃん! パターンが見える! ほらほら、縦読みすれば!」
僕「ほんとだ!」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 420本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第101回終わり)
(2015年1月9日)
この記事は『数学ガールの秘密ノート/ビットとバイナリー』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!