![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/行列が描くもの』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。僕のことを《お兄ちゃん》と呼ぶ。
ユーリ「ねー、お兄ちゃん。ゼロって何?」
僕「なんだよ、いきなり」
ユーリ「いーから! ねー、ゼロっていったい何?」
僕「ゼロは……ゼロだよ。数の $0$ のことだろ?」
ユーリ「他にゼロなんてないよ」
僕「$0$ とは何か。それはいろんな説明の仕方があるよ。 たとえば、《どんな数 $a$ に加えても、値が変わらない数のこと》とかね。 つまりそれは、 $$ a + 0 = a $$ になるような数がゼロだといってるわけだけど」
ユーリ「うーん」
僕「他にもあるよ。《どんな数 $a$ に掛けても、それ自身になってしまう数のこと》 とか。つまりそれは、 $$ a \times 0 = 0 $$ になるような数がゼロだと」
ユーリ「まーそーだけど」
僕「ゼロは大事な数だよ。足し算の話をするなら、正の数から負の数を作るときはゼロを使ったよね。 つまり、 $a > 0$ のとき、 $$ a + a' = 0 $$ になるような $a'$ として $-a$ を作ったわけだ」
ユーリ「……」
僕「掛け算でもゼロは重要だよ。 $a \times b = 0$ という式ができたら、 $a = 0$ または $b = 0$ になる。これは重要な性質だよ。 方程式を解くときにこれを使う」
ユーリ「おっと! それそれ! その話もっと聞きたい!」
僕「え? 何で急に食いついてきたんだ?」
ユーリ「いーから、いまの話もっぺん!」
僕「掛け算でのゼロは重要だという話? つまり、こういうことだよ。 $a \times b$ はふつうは $ab$ と書くから……」
$$ ab = 0 \LEFTRIGHTARROW a = 0 \MATAWA b = 0 $$ユーリ「うん、これ知ってる。どっちかはゼロってことでしょ?」
僕「そうだね。 $ab = 0$ ならば、 $a = 0$ または $b = 0$ が成り立っている。 つまり、 $a$ か $b$ か、少なくともどちらか片方は $0$ に等しい」
ユーリ「両方 $0$ でもいーんでしょ?」
僕「もちろん。いま言ったのは、右向きの《ならば》の話。つまり、 $$ ab = 0 \RIGHTARROW a = 0 \MATAWA b = 0 $$ の話だね。 $ab = 0$ ならば、何がいえるかを考えた。 この逆、つまり左向きの《ならば》もいえる。つまり、 $$ ab = 0 \LEFTARROW a = 0 \MATAWA b = 0 $$ ということ。 $a$ と $b$ の少なくともどちらか片方が $0$ に等しかったら、積 $ab = 0$ が成り立つ」
ユーリ「あいかわらずくどいけど、わかってるよん」
僕「がく。そしてこのことは、たとえば $x^2 - 5x + 6 = 0$ みたいな方程式を解くときに使うね」
ユーリ「因数分解でしょ? できるできる!」
$$ \begin{align*} x^2 -5x + 6 &= 0 \\ (x - 2)(x - 3) &= 0 && \REMTEXT{左辺を因数分解した} \\ \end{align*} $$僕「そうそう。 《因数分解をする》というのは《積の形にする》ということ。 そしてなぜ積の形にしたかというと……さっきの $$ ab = 0 \LEFTRIGHTARROW a = 0 \MATAWA b = 0 $$ を使いたいからだよね」
$$ (x - 2)(x - 3) = 0 \LEFTRIGHTARROW x - 2 = 0 \MATAWA x - 3 = 0 $$ユーリ「$x = 2, 3$ でしょ?」
僕「そうだね。ていねいに書くなら《$x = 2$ または $x = 3$》になる。 $x^2 - 5x + 6 = 0$ という《和の形》だとよく見えなかったけれど、 $(x - 2)(x - 3) = 0$ という《積の形》だと、方程式の解がよく見える……でも、 ユーリはもうこんな話はわかってるだろ? 何を考えてるんだ?」
ユーリ「あのね、こないだね、友達が学校で変なこと言ってたの」
僕「例のボーイフレンド」
ユーリ「違うって!……こういう数があるっていう話。こんな数、あるの?」
こんな数、あるの?
《$AB$ がゼロなのに、 $A$ と $B$ の両方ともゼロとはかぎらないような数》
僕「積がゼロなのに、どちらもゼロとは限らない数ということ?」
ユーリ「そー! そんな数、ないって言ったんだけど、 《あいつ》は《作ればいい》って言うんだよ。《数を作る》って、どゆこと?」
僕「《数を作る》って? ああ、まあ、そうだね。 僕たちがふだん使っている《数》とは違うけれど、 そういう数のようなものを定義することはできるね。 たとえば《行列》はそうなるな」
ユーリ「ぎょうれつ? なにそれ」
僕「数のように足したり引いたり掛けたりできるものだね。 積はゼロだけど、それぞれはゼロじゃないことがある。 うん、確かに」
ユーリ「数みたいだけど、数じゃない数?」
僕「行列はもう勉強したから説明できるよ。最初から説明しようか?」
ユーリ「ユーリにもわかる? 難しくない?」
僕「だいじょうぶ。数とは違う不思議な感覚がしておもしろいよ」
ユーリ「へー!」
僕「じゃ、行列の簡単な例から話していくよ」
ユーリ「あ、ちょっと待って」
僕「がく」
ユーリ「あのね。《数を作る》ってどーゆーこと?」
僕「うん、だから、いまからその話をするんだよ。 《数を作る》というか、数に似ているけれど普通の数とは違うものを作るというか。 とにかく、全部《定義》していくから大丈夫」
ユーリ「てーぎ」
僕「そうだよ。自分で定義してしまえばいい。 数学に出てくるものは全部そうやって作るんだから」
ユーリ「数も?」
僕「そうだね」
ユーリ「うーん……ま、いーや。ではセンセー、始めて」
僕「まず、行列の簡単な例から話すね。 こんなふうに数を並べたものを行列という」
行列の例 $$ \left(\begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right) $$
ユーリ「いち、に、さん、よん」
僕「そうだね。 $1,2,3,4$ のところに書くのはどんな数でもいいんだけど、 とにかくこんなふうに並べる」
ユーリ「へー」
僕「上の $1\quad 2$ のところを《$1$ 行目》といって、次の $3\quad 4$ のところを《$2$ 行目》という」
ユーリ「はー」
僕「そして、左に縦にならんでいる $\begin{array}{c}1\\3\end{array}$ のことを《$1$ 列目》といって……」
ユーリ「次の $\begin{array}{c}2\\4\end{array}$ が《$2$ 列目》でしょ?」
僕「そういうこと。難しくないだろ?」
ユーリ「難しくないけど、面白くもない」
僕「そうだよね。横に並んでいる数を《行》といって、 縦に並んでいる数のことを《列》というってだけの話だから」
ユーリ「ああ、行と列があるから《行列》なの?」
僕「そうだね。 $1,2,3,4$ の代わりに別の数を入れたものも、 ぜんぶ行列の例になるよ。こんなふうに」
さまざまな行列
$$ \left(\begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right) \qquad \left(\begin{array}{cc} 3 & 1 \\ 4 & 1 \end{array} \right) \qquad \left(\begin{array}{cc} 10 & 21 \\ \tfrac12 & -4.25 \end{array} \right) $$
ユーリ「ふんふん?」
僕「いま書いたのは全部、 $2$ 行と $2$ 列からできている行列で、 これを《$2\times2$ 行列》と呼ぶ。でも、行列は何行何列あってもいい」
行と列の数がさまざまな行列
$$ \left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{array} \right) \quad \REMTEXT{$3\times3$行列} $$
$$ \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ \end{array} \right) \quad \REMTEXT{$2\times4$行列} $$
$$ \left( \begin{array}{c} 1 \\ 2 \\ \end{array} \right) \quad \REMTEXT{$2\times1$行列} $$
ユーリ「はいはい。ぜんぜん難しくないじゃん」
僕「言っただろ?」
ユーリ「むー」
僕「まとめると、これが行列……ここでは $2 \times 2$ 行列の定義」
$2 \times 2$ 行列
$a,b,c,d$ を数とするとき、 $$ \left(\begin{array}{cc} a & b \\ c & d \end{array} \right) $$ を $2 \times 2$ 行列という。
僕「ここからは $2 \times 2$ 行列だけを使って説明するね」
ユーリ「早く、数……みたいなものを作ってほしいんだけど」
僕「うん。いまから作るよ。 数だとすれば、足し算引き算をしたくなる。 だから《行列と行列の足し算》を定義してやればいい。 つまり《行列の和》を定義するということ」
行列の和
$$ \left(\begin{array}{cc} a_1 & b_1 \\ c_1 & d_1 \end{array} \right) + \left(\begin{array}{cc} a_2 & b_2 \\ c_2 & d_2 \end{array} \right) = \left(\begin{array}{cc} a_1+a_2 & b_1+b_2 \\ c_1+c_2 & d_1+d_2 \end{array} \right) $$
僕「ね。これで定義できただろ?」
ユーリ「『ね』とか言われても、わかんないよ! こんな式だけ出されてもさー」
僕「ユーリは《わかんない!》とはっきり言ってくれるから話しやすいな。 まず、 $a_1,b_1,c_1,d_1$ や $a_2,b_2,c_2,d_2$ などはぜんぶ数だとしよう。 そうすると、これは行列だよね?」
$$ \left(\begin{array}{cc} a_1 & b_1 \\ c_1 & d_1 \end{array} \right) $$ユーリ「そだね。数並べてるから」
僕「いまから僕たちは《行列の和》を定義したい。 つまり、次の式が何を意味しているかを決めたいということ」
この式は何を意味しているか
$$ \left(\begin{array}{cc} a_1 & b_1 \\ c_1 & d_1 \end{array} \right) + \left(\begin{array}{cc} a_2 & b_2 \\ c_2 & d_2 \end{array} \right) $$
ユーリ「何を意味してるかって……足してるんじゃないの?」
僕「そうだね。でも、僕たちは《数の足し算》は知ってるけど、 《行列の足し算》は知らない。お兄ちゃんは知ってるけど、ユーリは知らない」
ユーリ「うん」
僕「だからこの《行列の足し算》 $\left(\begin{array}{cc} a_1 & b_1 \\ c_1 & d_1 \end{array} \right) + \left(\begin{array}{cc} a_2 & b_2 \\ c_2 & d_2 \end{array} \right)$ の意味を、《数の足し算》を使って定義してみよう。 それがさっき書いたこの式なんだ」
行列の和
$$ \left(\begin{array}{cc} a_1 & b_1 \\ c_1 & d_1 \end{array} \right) + \left(\begin{array}{cc} a_2 & b_2 \\ c_2 & d_2 \end{array} \right) = \left(\begin{array}{cc} a_1+a_2 & b_1+b_2 \\ c_1+c_2 & d_1+d_2 \end{array} \right) $$
ユーリ「なんとなくわかった……かも? でもまだバシッとはわかってない」
僕「行列 $\left(\begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right)$ の中に書かれている数 $1,2,3,4$ のことを、 この行列の《成分》っていうんだ。《要素》というときもあるかな。 $\left(\begin{array}{cc} a & b \\ c & d \end{array} \right)$ の成分は何だかわかる?」
ユーリ「何って……そりゃ、 $a,b,c,d$ じゃないの?」
僕「そうだね。成分という言葉を使えば《行列の和》は、 《《成分同士の和》を成分とする行列》として定義できるわけだ」
《行列の和》は《《成分同士の和》を成分とする行列》として定義する
$$ \left(\begin{array}{cc} a_1 & b_1 \\ c_1 & d_1 \end{array} \right) + \left(\begin{array}{cc} a_2 & b_2 \\ c_2 & d_2 \end{array} \right) = \left(\begin{array}{cc} a_1+a_2 & b_1+b_2 \\ c_1+c_2 & d_1+d_2 \end{array} \right) $$
ユーリ「成分同士の和っていうのは、 $a_1+a_2$ のこと?」
僕「そうだね! 右辺に書いてあるような、 $a_1+a_2, b_1+b_2, c_1+c_2, d_1+d_2$ という四つの数を成分とする行列が、 左辺の二つの行列の和になるわけだ」
ユーリ「なんで?」
僕「いや、これは定義だから、理由はないんだよ。 このように決めました……決めてみましたよ、定めてみましたよ、 こういうルールにしてみましたよ、ということ」
ユーリ「ルールを作ったってこと?」
僕「まさにそうだよ。ルールを作ったってこと。 行列の和を求めるためのルールを作った。 計算方法を決めたといってもいいかな」
ユーリ「そんなの……決めてもいいの?」
僕「決めてもいいよ。でも、めちゃめちゃなルールだと困るから、 《一貫性》や《整合性》が必要になるね」
ユーリ「よくわかんない」
僕「その話の前に、一つだけ計算練習してみようか。行列の足し算練習に挑戦!」
ユーリ「何ハイになってんの?」
問題
次の行列の和を求めよ。
$$ \left(\begin{array}{cc} 10 & 20 \\ 30 & 40 \end{array} \right) + \left(\begin{array}{cc} 5 & 3 \\ -10 & 0 \end{array} \right) $$

僕「これは計算できる?」
ユーリ「カンタンじゃん。だって、数を足せばいーんでしょ?」
僕「成分同士」
ユーリ「あー、はいはい。成分同士を足せばいーんでしょ? だから……」
$$ \begin{align*} \left(\begin{array}{cc} 10 & 20 \\ 30 & 40 \end{array} \right) + \left(\begin{array}{cc} 5 & 3 \\ -10 & 0 \end{array} \right) &= \left(\begin{array}{cc} 10+5 & 20+3 \\ 30-10 & 40+0 \end{array} \right) \\ &= \left(\begin{array}{cc} 15 & 23 \\ 20 & 40 \end{array} \right) \\ \end{align*} $$ユーリ「だから、行列の和は $\left(\begin{array}{cc} 15 & 23 \\ 20 & 40 \end{array} \right)$ だね!」
僕「はい、答えは正解です」
ユーリ「引っかかる言い方」
僕「途中の計算で、 $30-10$ ってやってたけど、 あれは $30+(-10)$ のつもりで書いたんだよね?」
ユーリ「え、あ? あー、はいはい。そーだよん。もちろん。 だって、成分同士の和だもん! (意識してなかったケド……)」
僕「細かい話だけど、定義通りに考えるとしたら、 $30+(-10)$ のように和にするわけだね。 もちろん結果は同じ」
ユーリ「ふーん」
解答
$$ \left(\begin{array}{cc} 10 & 20 \\ 30 & 40 \end{array} \right) + \left(\begin{array}{cc} 5 & 3 \\ -10 & 0 \end{array} \right) = \left(\begin{array}{cc} 15 & 23 \\ 20 & 40 \end{array} \right) $$
僕「難しくないだろ?」
ユーリ「難しくないけど、やっぱりそれほど面白くもない」
僕「これで《行列の和》ができた。 つまり、行列同士で $+$ という計算ができるようになったわけだ。 《数の和》のための $+$ を使って、《行列の和》のための $+$ を定義したともいえる」

ユーリ「ほほー! 同じプラスなのに違う意味!」
僕「じゃ、次は《行列の差》を定義してみよう」
ユーリ「《行列の差》を定義しよう……って、引き算すればいいんじゃないの?」
僕「何の?」
ユーリ「あー、はいはい。《成分同士の引き算》ね。 お兄ちゃんってそういう《先生トーク》よくやるよね」
僕「《先生トーク》って何だろう」
ユーリ「自分は答えを知ってて、ユーリが何かまちがったこというと、 聞き返すの。『何の?』とか『そうかな?』とか『その理由は?』とかね。 それって、すんごくセンセイっぽい」
僕「そんなにしょっちゅうは聞き返さないと思うけどなあ」
ユーリ「《行列の差》はこれで定義できるでしょ?」
《行列の差》は《《成分同士の差》を成分とする行列》として定義する
$$ \left(\begin{array}{cc} a_1 & b_1 \\ c_1 & d_1 \end{array} \right) - \left(\begin{array}{cc} a_2 & b_2 \\ c_2 & d_2 \end{array} \right) = \left(\begin{array}{cc} a_1-a_2 & b_1-b_2 \\ c_1-c_2 & d_1-d_2 \end{array} \right) $$
僕「そうだね。それでいい。計算練習はしなくてもいいよね。 さあ、これで準備ができたよ!」
ユーリ「準備って……何の?」
僕「ゼロを作る準備だよ、もちろん」
ユーリ「ゼロを……作る?」
僕「いま僕たちは数を……数のようなものを作っているんだよね。 行列というものを用意して、和と差は定義できた。 成分の和と差で定義した。 さあ、ここでユーリの発想が光るときだよ! 《行列の世界でゼロに相当するもの》を定義するにはどうしたらいいだろう」
ユーリ「行列の……ゼロ」
僕「そうだね。零行列という名前で呼ばれているものがあるんだけど、 それはどんな姿をしているんだろうか」
ユーリ「たぶん、成分がぜんぶ $0$ の行列?」
僕「それは、こういう行列のこと?」
$$ \left(\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right) $$ユーリ「うん、そう」
僕「なぜユーリはそう思ったの?」
ユーリ「あー、まちがったかー!」
僕「え?」
ユーリ「まちがいなんでしょ。だって、ほら、聞き返してきたじゃん。 正解だったら、お兄ちゃんは『正解です!ユーリは賢いなあ!』ってゆーもん」
僕「いやいや、ユーリの考えは正解だよ」
ユーリ「え? そなの? $\left(\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right)$ がゼロでいいの?」
僕「そうだよ。 $\left(\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right)$ が零行列だ」
零行列
$$ \left(\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right) $$
ユーリ「じゃ、なんで聞き返したの? 『なんでそう思ったか』って」
僕「知りたかったからだよ。ユーリが $\left(\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right)$ を零行列だと思った根拠を」
ユーリ「根拠ったって……それっぽいし、だって、そう定義すればいーんでしょ。 理由はいらないって言ったじゃん」
僕「確かにね。でも、《一貫性》や《整合性》は必要になる」
ユーリ「だから、それ意味わかんないって」
僕「つまりね、ユーリの疑問がここで輝いてくるんだよ。 ユーリはさっき言ったじゃないか。『ゼロって何だろう』って」
ユーリ「うん」
僕「数の場合のゼロはどんな性質を持っていたかというと……」
ユーリ「数のゼロは、足しても変わんない」
僕「そうだね。どんな数 $a$ に対しても $0$ を足しても変わらない。 $a + 0 = a$ になる。 $0$ にはそういう性質がある」
ユーリ「あ! わかったわかったわかった! 行列もおんなじじゃん!」
零行列の性質
$$ \left(\begin{array}{cc} a & b \\ c & d \end{array} \right) + \left(\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right) = \left(\begin{array}{cc} a & b \\ c & d \end{array} \right) $$
僕「そうだね。どんな行列に対して $\left(\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right)$ を足しても変わらない。 そんな行列だから、これを零行列としよう。数との一貫性があってうれしい」
ユーリ「んー、でも変わんないのはあたりまえだよね。成分に $0$ を足してるだけだから」
僕「そうだね。ねえ、ユーリって、わからないときにはわからないって言うよね」
ユーリ「うん?」
僕「そして、ちゃんと理解したら喜ぶ。そういうのを積み重ねているから、 《あたりまえ》だっていえるんだと思うな。一歩一歩をきちんと進めている。 ユーリは偉いぞ」
ユーリ「照れるじゃん」
僕「ところで、もう一つ。 等しい行列が二つあって、その差を求めたとしよう。 どうなるだろう」
ユーリ「行列の差って、成分同士引き算すればいーんだから、 ゼロになるんじゃないの?」
僕「何が?」
ユーリ「……成分が全部 $0$ になるんでしょ? あ、零行列になるっていえばいいのか」
僕「そうだね」
等しい行列の差は零行列になる
$$ \left(\begin{array}{cc} a & b \\ c & d \end{array} \right) - \left(\begin{array}{cc} a & b \\ c & d \end{array} \right) = \left(\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right) $$
ユーリ「あっ! これも数とおんなじ! $a - a = 0$ だもん」
僕「そうそう。これもあたりまえのことだけど、《行列の和と、差と、零行列》は、 《数の和と、差と、 $0$》とよく似ているわけだね。ここまでで、 行列に対する $+$ と $-$ がよくわかっただろ」
ユーリ「カンタンすぎ! 行列に対する $+$ と $-$ なんて、そのまんまじゃん……あれ?」
僕「何かおかしい?」
ユーリ「イコールは? 行列に対するイコール($=$)って定義してないじゃん」
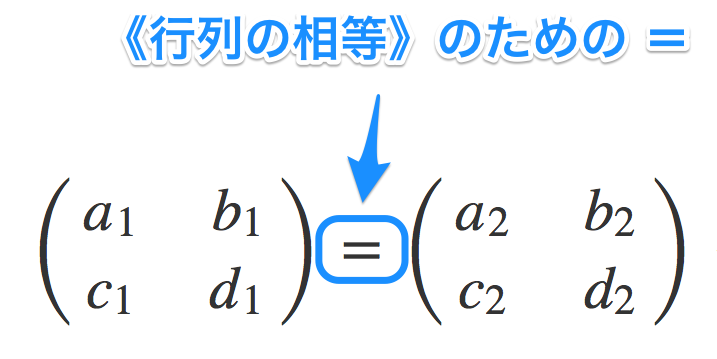
僕「おおっと、そうだね。ユーリは賢いなあ。 二つの行列が等しいとはどういうことかを定義してなかったね。 ほんとうはこれを一番最初に定義しなきゃいけなかったんだ。 《行列の相等》」
行列の相等
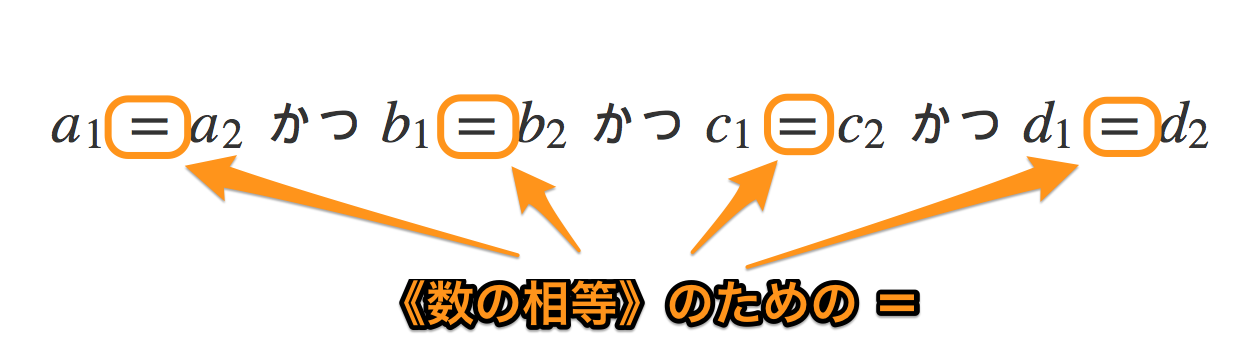
$$ \begin{align*} \left(\begin{array}{cc} a_1 & b_1 \\ c_1 & d_1 \end{array} \right) = \left(\begin{array}{cc} a_2 & b_2 \\ c_2 & d_2 \end{array} \right) \LEFTRIGHTARROW a_1 = a_2 \KATSU b_1 = b_2 \KATSU c_1 = c_2 \KATSU d_1 = d_2 \end{align*} $$
ユーリ「ふんふん。これは《成分同士が等しい》という意味だね?」
僕「その通り。《数の相等》のためのイコールを使って、《行列の相等》のためのイコールを定義したんだよ」
僕「これで、行列の相等($=$)と和($+$)と差($-$)が定義できて、 零行列 $\left(\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right)$ も定義できたね。 つまり、これで、等しいかどうかを調べることと、 足し算と、引き算ができる《数のようなもの》を作ったことになる。 ゼロも作った」
ユーリ「にゃるほど。ねえ、じゃ、次は? 次は何を作るの?」
僕「それはもちろん、アレだよ」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 420本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第111回終わり)
(2015年4月3日)
この記事は『数学ガールの秘密ノート/行列が描くもの』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!