第201回 シーズン21 エピソード1

最初に最後を考えて（前編） ただいま無料

僕の部屋

ユーリ「あー、退屈退屈ー！」

僕「人の部屋に遊びに来ておいて、退屈を連発するのはないよなあ」

ユーリ「だって、退屈だもん。ねー、お兄ちゃん。なんかおもしろいことないの？　クイズとかパズルとか」

僕「そんなこと急に言われてもね」

ユーリ「あっ！　それじゃゲームしよゲーム！　オセロとか」

僕「オセロねえ……あんまり」

ユーリ「お兄ちゃん、なにげに弱いもんね（『数学ガールの秘密ノート／数列の広場』参照）」

僕「それに、ほら、オセロは登録商標だし」

ユーリ「理由になってなーい！」

僕「うん、じゃあ、こんなゲームをしようか。単純だけどおもしろいよ」

ユーリ「なになに、どんなの？」

ゲーム

僕「うん、まず最初にジャンケンで先攻後攻を決めよう。ジャンケン……」

ユーリ「ポン！」

僕「ユーリがチョキで僕がパーだから、ユーリが先攻だね」

ユーリ「そんでそんで？」

僕「ちょっと待って、準備するから」

ユーリ「ふむふむ？」

僕「このマルを交互に消していくんだ。何個消すかは自分で選べるけど、 必ず $1$ 個は消さなくちゃいけない。それから、 $4$ 個以上消しちゃだめ」

ユーリ「消す数は $1,2,3$ 個のどれかってこと？」

僕「そういうこと。かわりばんこに消していって、最後のマルを消した人の負け」

ユーリ「オッケー、わかった！　何個消そうかな……」

僕「それから、何個消すかを決めるのに時間を掛けちゃだめ」

ユーリ「時間？」

僕「相手が $10,9,8,\ldots$ とカウントダウンしていって、 $0$ になるまでに消すこと。もたもたしちゃだめだよ。 じゃあ、スタート！　 $10,9,8,\ldots$」

ユーリ「えっ、ええええっ……えーっと！」

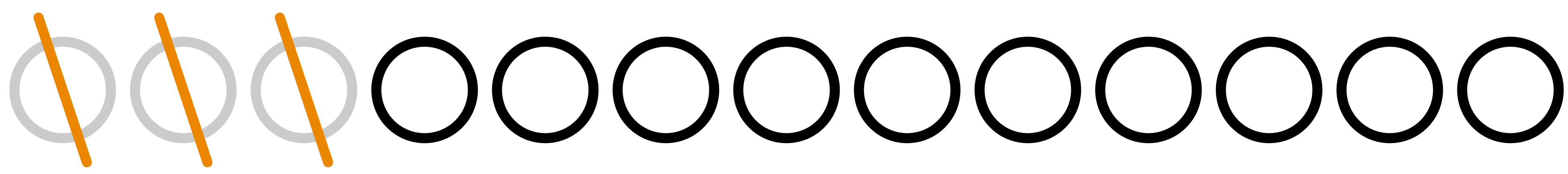
僕「$3$ 個消したんだね。じゃ、今度は僕が消す番だ」

ユーリ「急にカウントダウン始めるの、ずるいよー。 $10,9,8,7,6,5,4,3,2,1,0$ 　はい時間！はい時間！」

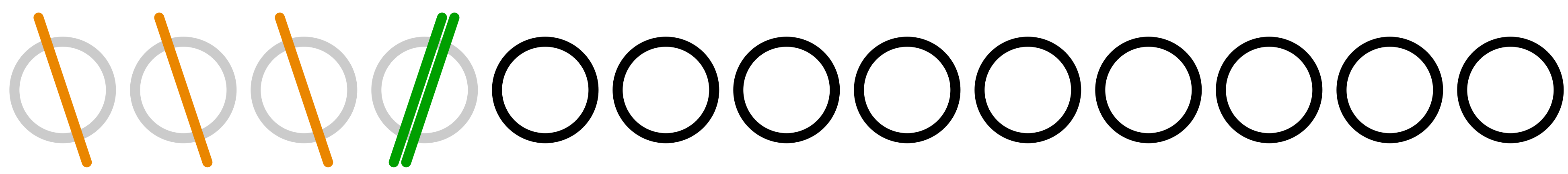
僕「ずるいと言いながら、そんなに早口でカウントダウンするなよ、ユーリ」

ユーリ「へへー」

僕「じゃ、ユーリの番だよ。 $10,9,8,7,6,5,4,3,2,1,0$ 　はい、消した？」

ユーリ「お兄ちゃんだって、早口じゃん！　いま消す！」

僕「消したね」

ユーリ「$10,9,8$」

僕「消したよ」

ユーリ「え？　もー消したの？」

僕「$10,9,8,7,6,5$」

ユーリ「待って待って！……残りが少ない！　はい、消した！」

僕「はい、消したよ」

ユーリ「あっ……最後の $1$ 個……」

僕「ということで、最後に $1$ 個残ったマルを消したユーリの負け！　今回の勝負は僕の勝ち！」

ユーリ「なんだそりゃー！！」

ユーリ「うー！　スリルあっておもしろいけど、負けたのはくやしー！　だいたい、ルール説明直後すぐにカウントダウン始めるのってずるくない？」

僕「でも、もう様子はわかっただろ？」

ユーリ「わかった。もっかいやる！」

第2回戦

僕「じゃあ、もう一回、先攻後攻決めるジャンケンしようか。公平にね」

ユーリ「お兄ちゃんが先に消すんだね」

僕「ちょっと待って、準備するから」

ユーリ「じゃ、いっくよー！　 $10,9,\ldots$」

僕「はい、消した」

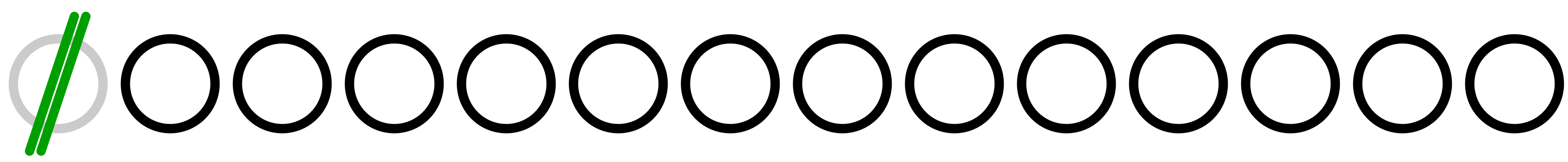
ユーリ「早っ！」

僕「$10,9,8,7,6,5,4,3,2,1,0$ 　消した？」

ユーリ「消したよん」

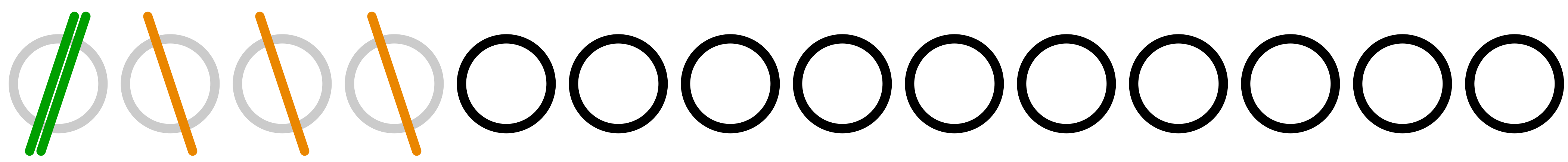
僕「はい消した」

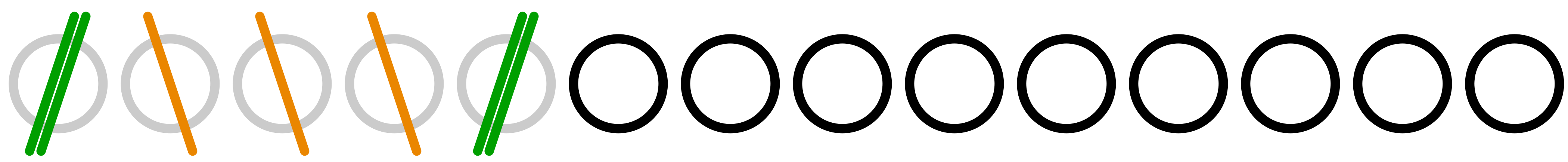
ユーリ「何でそんなに早いの？　まだカウントダウンしてないよっ！」

僕「ということで、ユーリの負け」

ユーリ「……」

僕「第3回戦、やる？　もう飽きた？」

ユーリ「……むー。もっかいやる」

僕「じゃ、また、先攻後攻をジャンケンで決めようか。公平に……」

ユーリ「ダウト」

僕「何がダウト？」

ユーリ「お兄ちゃん！　ユーリの目はごまかせませんぜ。なんだか変！　お兄ちゃんが必ず勝つようなトリックがある！」

僕「ジャンケンにトリック？」

ユーリ「ちがう……そうじゃなくて、 お兄ちゃんは、ジャンケンして先攻後攻を決めた後になってから、マルを書いてるよね。二回とも」

僕「ぎく」

ユーリ「さっきの紙、もっかい見せて！」

僕「……」

ユーリ「ねー、お兄ちゃん。ユーリ先攻のときはマルが $13$ 個でスタートしたけど、 ユーリ後攻のときはマルが $14$ 個でスタートしてるよねー。これは？」

僕「よく気がついたなあ」

ユーリ「……待って待って。し・か・も、ユーリ後攻の第2回戦で、お兄ちゃんはさっさとマルを $1$ 個消したよね。 ってことは、ユーリの番でマルは $13$ 個になってる。これって第1回戦と同じ状態じゃん！　さー、正直に言っちまいな。何を企んだのかね？」

僕「はいはい、正直に説明しますよ。ユーリ探偵。このゲームは《残り $13$ 個で相手の番にしたら必ず勝てる》んだよ。 つまり、必勝法が存在するってことだね」

ユーリ「ひっしょうほう！　必ず勝つ方法！　何それひどーい！　いたいけな乙女を惑わすなんてしくしく……」

僕「探偵じゃなかったのか」

ユーリ「乙女な探偵なの！　……でも、なんで《残り $13$ 個で相手の番にしたら必ず勝てる》の？　 $13$ ってそんな不思議な数なの？」

僕「それが問題になる」

ユーリ「わかった！　 $13$ だけじゃないね、お兄ちゃん！」

僕「わかった？」

ユーリ「わかった。 $$ 1,5,9,13 $$ なんでしょ？」

僕「その通りだね。名探偵ユーリは、謎をすべて解いたのかな？」

ユーリ「解いたよん！」

僕「『名探偵、皆を集めてさてと言い』」

ユーリ「何それ……あのね、最初に、最後を考えたの」

僕「最初に最後を考える？」

ユーリ「最後にどうなったら勝つかを考えるの。最後の $1$ 個を消した人が負けるんだから、 《最後の $1$ 個を相手に消させたら勝つ》わけでしょ？　相手の番で、残りが $1$ 個なら、自分が勝つ」

僕「うん、そうなるね」

ユーリ「てことは、自分の番で残りが $2$ 個、 $3$ 個、 $4$ 個のどれかになってれば、勝てる。 だって、自分の番で残りが $2$ 個なら $1$ 個消す、 $3$ 個なら $2$ 個消す、 $4$ 個なら $3$ 個消せばいいもん。 そーすれば、相手に最後の $1$ 個を押しつけられる」

僕「いいねえ」

ユーリ「自分の番で残りが $2,3,4$ 個になってれば勝てるんだから、 《相手の番で $5$ 個にすれば勝つ》わけでしょ」

僕「それはどうして？」

ユーリ「だって、相手の番で残り $5$ 個だったら、相手が $1$ 個消したら残り $4$ 個、 $2$ 個消したら残り $3$ 個、 $3$ 個消したら残り $2$ 個だけど、 残り $4,3,2$ 個のどれでも、自分の番で残り $1$ 個にできるから」

僕「いいねえ。ユーリの推理はすばらしいな！」

ユーリ「えへへ。あとはその繰り返しでしょ。 $4$ 個ずつ増やしていけばいい！」

• 相手の番で残り $1$ 個なら、自分が勝つ。
• 相手の番で残り $5$ 個なら、自分が勝てる。
• 相手の番で残り $9$ 個なら、自分が勝てる。
• 相手の番で残り $13$ 個なら、自分が勝てる。

僕「……」

ユーリ「ジャンケンで公平に見せかけておいて、 ユーリが先攻になったら、 $13$ 個のマルを書く。 ユーリが後攻になったら、 $14$ 個のマルを書いておいて、お兄ちゃんはすぐに $1$ 個消す！」

僕「……」

ユーリ「お兄ちゃんは、 $1,5,9,13$ ってゆー数を覚えてたんでしょ！ ユーリの番に回すときに、必ず $1,5,9,13$ になるよーに毎回残りの個数を数えてたんだ！　謎はすべて解けた！　反論はあるかね？」

僕「すばらしい名推理！　その通りなんだけど、一点だけ違うことがある」

ユーリ「何？」

僕「ユーリの番に回すときに、 $1,5,9,13$ になるように調整していたのは確かなんだけど、 毎回残りを数えていたわけじゃない。 $13$ にしてユーリに回した後は、《ユーリが消した数》と《自分が消す数》の合計が $4$ になるようにしていただけなんだよ。 ユーリが $1$ 個消したら自分は $3$ 個消す。ユーリが $2$ 個消したら自分は $2$ 個消す。 $3$ 個消したら自分は $1$ 個消す」

ユーリ「ほほー」

僕「毎回残りを数えていたら時間が掛かるだろ？　だから、いったん必勝パターンを作ったら、 相手の消した個数に合わせて自分の消す個数を決める方が早いんだ」

ユーリ「にゃるほど……」

僕「必勝法があるのに公平なふりしてごめんよ」

ユーリ「つーん……でも、おもしろかったからゆるしたげる。感謝したまえ」

僕「それはそれは、アリガタキシアワセ。 ところで、 $13$ 個じゃなくてもっと多い数から始めることもできるよ」

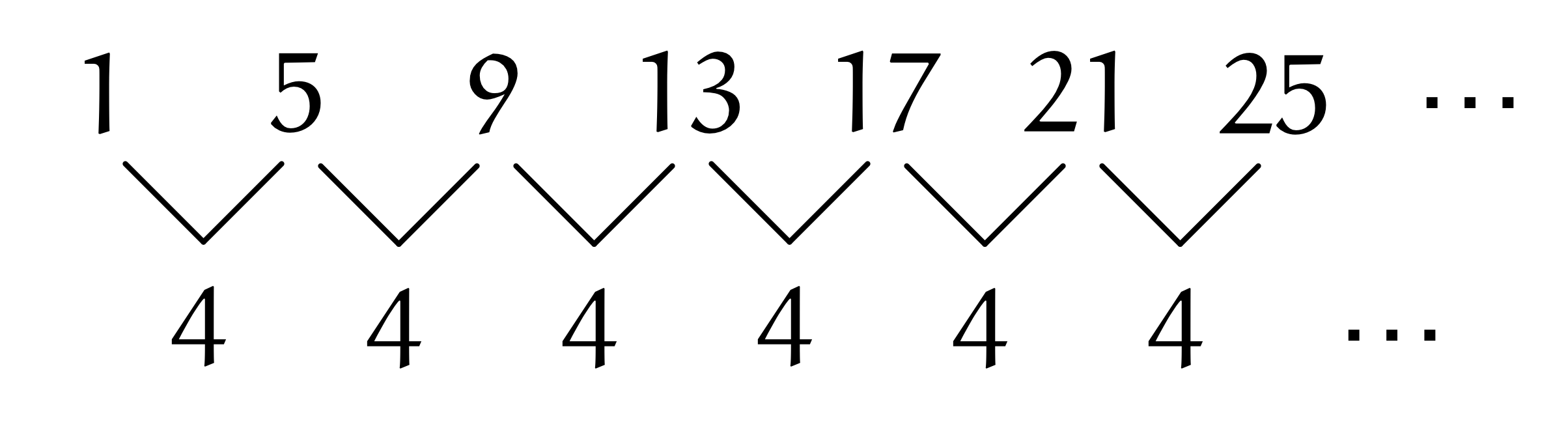
ユーリ「あー、そだね。 $4$ 個ずつ増やせばいーから、 $$ 1,5,9,13,17,21,25,\ldots $$ なんでしょ？」

僕「そういうことだね。一般的に書くなら、 《相手の番になったときに、残りの個数が $4n+1$ 個のとき》が必勝パターンといえるね」

ユーリ「出たな《一般化の帝王》」

僕「何その二つ名……」

ユーリ「だって、お兄ちゃんは必ず《一般化すると……》とか、 《一般的に書くと……》とか言うじゃん。だから、《一般化の帝王》」

僕「まあ、いいけどね。でも、 $$ 1,5,9,13,17,21,25,\ldots $$ のような数列を見ると、一般項を考えたくならない？　この数列は $1$ で始まって $4$ ずつ増えている、等差数列だよね」

ユーリ「ふんふん。 $4$ ずつ増えているってことは、階差数列が $4,4,4,4,4,4,\ldots$ になるやつだね！」

僕「そういうこと。ユーリは階差数列好きだよね」

ユーリ「好き好き。ユーリのことは《階差数列の女王》と呼びたまえ！」

僕「またわけのわからないことを……ともかく、この数列 $1,5,9,13,17,21,25,\ldots$ の一般項は、 $4n + 1$ として表せるわけだね」

ユーリ「いっぱんこう……ダウト？」

僕「え？　いやいや、 $4n + 1$ は間違いじゃないよ」

ユーリ「だって、最初は $1$ だよ？」

僕「ん？　……ああ、わかった。ユーリは $n = 1,2,3,\ldots$ で考えたんだね。 僕は $n = 0,1,2,3,\ldots$ で考えたんだ。ごめん。ふわふわっと言っちゃったね。ちゃんといえば、こういうこと」

ユーリ「あー、そゆことね。 $0$ から始めたんだ」

僕「学校で数列を習うときは $1$ から始めることが多いかも。 どちらでも同じことなんだけど、たとえば $1$ から始めてみようか」

ユーリ「にゃるほど。 $n = 0,1,2,3,\dots$ で考えたら $4n + 1$ で、 $n = 1,2,3,4,\ldots$ で考えたら $4n - 3$ で表せる」

僕「そういうことだね。こういうのは暗記するものじゃなくて、試すものだから」

ユーリ「？」

僕「自分が $n = 0,1,2,3,\ldots$ で考えていて、一般項が $4n + 1$ だなと思ったときには、 心の中で《ほんとにそうかな。 $n = 0$ のときちゃんと最初の $1$ が出てくるかな》と確かめるってことだよ。 自分が $n = 1,2,3,4,\ldots$ で考えているときには、 $4n - 3$ の $n$ に $1$ を代入してみて最初の $1$ が出てくるかを確かめる。 自分がうっかりミスしていないかどうかは、小さな数で試してみれば確かめられるね」

ユーリ「あー、はいはい。先生トーク先生トーク」

数列あれこれ

僕「さっきは、 $$ 1,5,9,13,17,21,25,\ldots $$ という数列を、 $$ \begin{align*} a_0 &= 1 \\ a_1 &= 5 \\ a_2 &= 9 \\ a_3 &= 13 \\ a_4 &= 17 \\ a_5 &= 21 \\ a_6 &= 25 \\ &\vdots \\ \end{align*} $$ と考えて、 $$ a_n = 4n + 1 $$ という一般項も出したけど、今度は別の数列を考えてみようか。そうだなあ」

ユーリ「わかった！　答えはフィボナッチ数列だ！」

僕「……まだ問題出してないよ」

ユーリ「だって、お兄ちゃんは、何かってゆーとフィボナッチ数列出してくるじゃん」

僕「はいはい。それはさておき、この数列の一般項はどう書けるだろう」

ユーリ「これはカンタンだよー。 $(-1)\times(-1) = 1$ を使うんでしょ？　えーっと、 $0$ 乗のとき $1$ になるから、 $$ c_n = (-1)^n $$ でいい？」

僕「はい、正解です」

ユーリ「やたっ！」

僕「もちろん、正解はひとつじゃないよ。たとえば、 $$ c_n = (-1)^{n+2} $$ だとしても、まちがいじゃない」

ユーリ「あ、そだね。でも $+2$ は無駄じゃん」

僕「ほかにはこんなのもできるね」

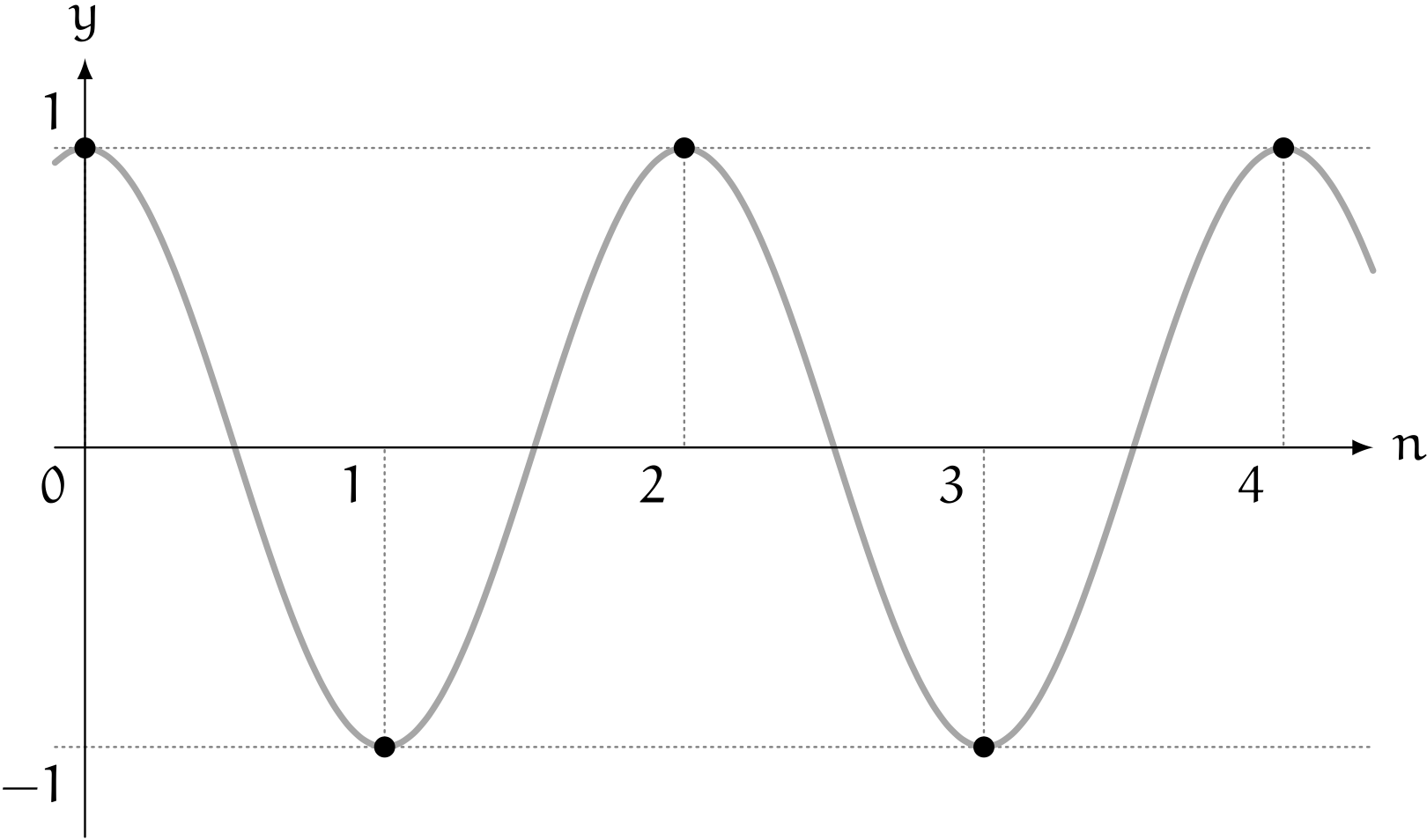
$$ c_n = \cos n\pi $$

ユーリ「突然コサイン出てきちゃった！」

僕「三角関数の $\sin$ や $\cos$ は、周期があって同じ値を繰り返し取るから、うまく調整してやると、 $1,-1,1,-1,1,-1,\ldots$ という繰り返しに合わせることもできるんだね」

ユーリ「だったら、サインでもできるの？」

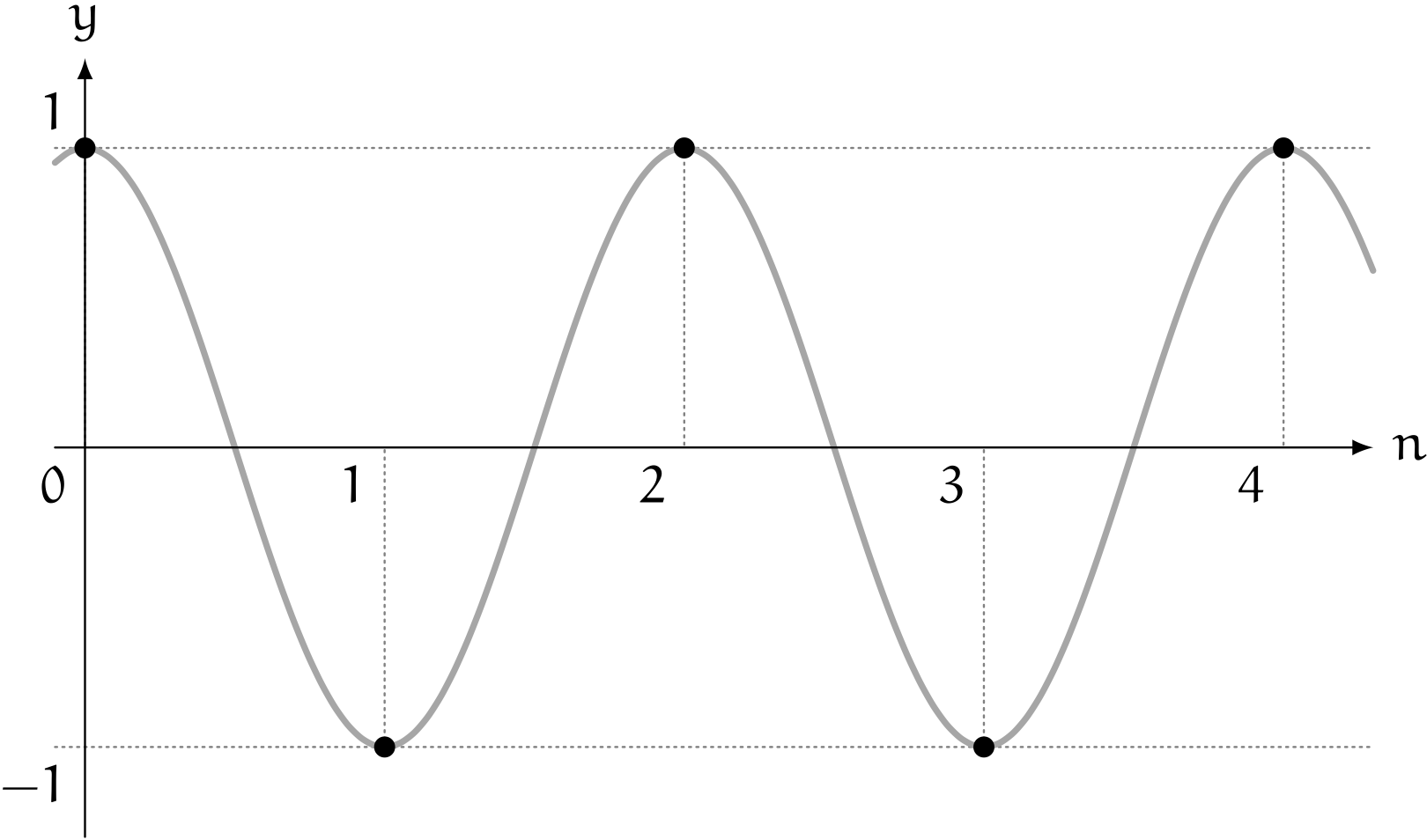
僕「できるよ。 $y = \sin x$ のグラフを描いて考えてみよう。 $y = 1$ になるところはどこにあるかな？」

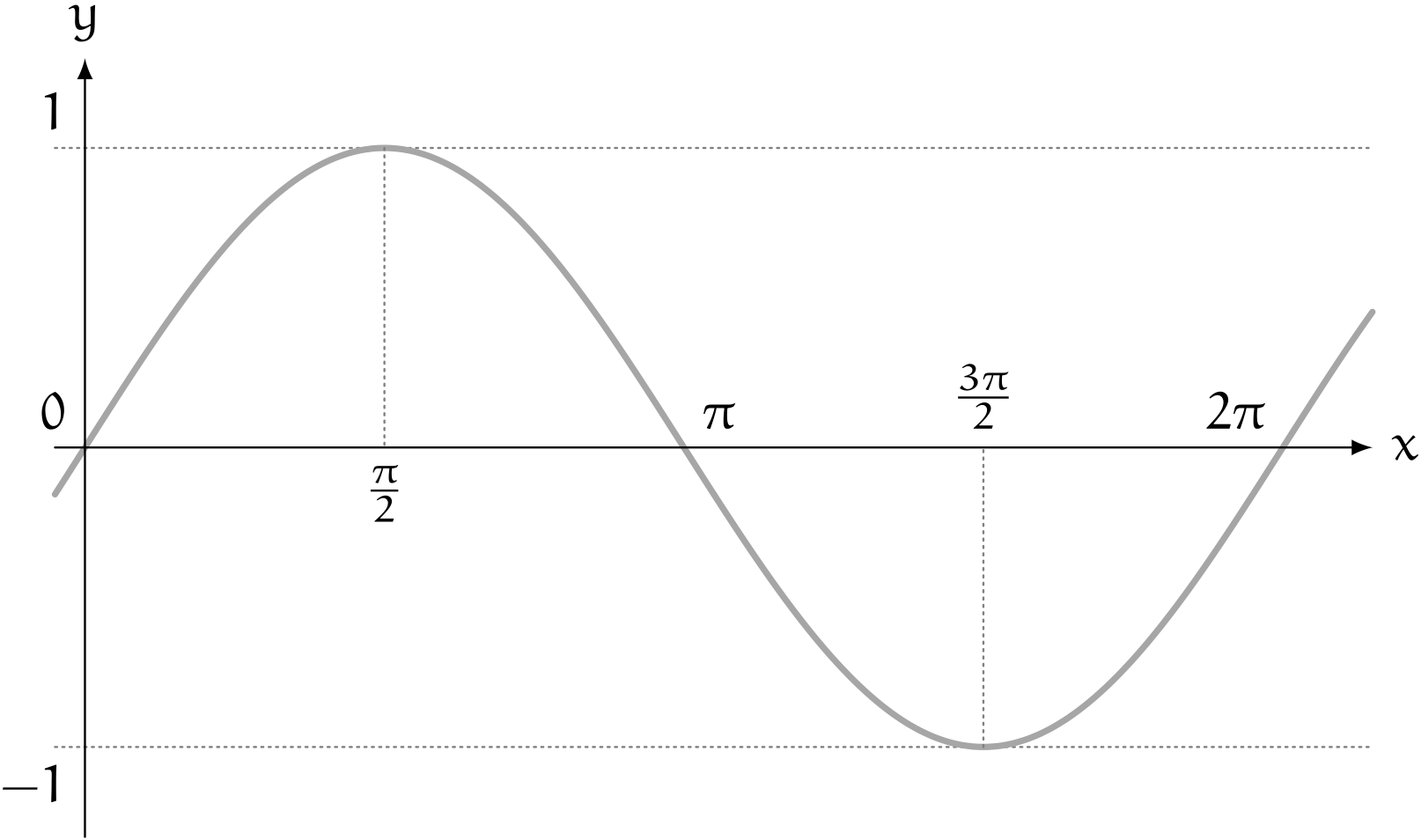
ユーリ「えーっと？　 $x = \frac{\pi}{2}$ で $y = 1$ になる？」

僕「そうだね。 $$ \sin \frac{\pi}{2} = 1 $$ で、 そこから $\pi$ だけ増やすと、 $$ \sin \frac{3\pi}{2} = -1 $$ になる」

ユーリ「……」

僕「$x = \frac{\pi}{2}$ からスタートして、 $x$ が $\pi$ 増えるたびに、 $\sin x$ は $1$ と $-1$ を繰り返す。 だから、 $n$ が $1$ 増えるたびに $x$ が $\pi$ 増えるようにしてやればいい。 ということで、 $$ c_n = \sin \left(n\pi + \frac{\pi}{2}\right) $$ にすれば、 $1,-1,1,-1,\ldots$ という数列を $\sin$ で書いたことになるね。結局それは $\cos n\pi$ と同じ形のグラフになるんだけどね」

ユーリ「……」

僕「……」

ユーリ「……なんか、似てる」

僕「？」

ユーリ「いまの話、さっきの話と、似てる」

僕「さっきの話？」

ユーリ「$n$が$1$増えたら$4$増えるような数列のとき、$4n+\REMTEXT{なんとか}$ってゆー式を考えたよね？」

僕「そうだね」

ユーリ「そして、 $n = 0$ のときにうまく $1$ になるように、 $4n + 1$ って式を作った」

僕「うん」

ユーリ「サインでも同じことやってる。$n$が$1$増えたら$\pi$増えるようにするために、$n\pi+\REMTEXT{なんとか}$ってゆー式にして、 それで……」

僕「うんうん。それで？」

ユーリ「それで、 $n = 0$ のときにうまく $\frac{\pi}{2}$ になるように、 $n\pi + \frac{\pi}{2}$ って式を作った……」

僕「そうだね。どちらも《何倍かして何かを足す》という形になってる。ユーリのいう通り、似ているね！」