![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ここは僕の部屋。いまは土曜日。
いとこのユーリがいつものように遊びに来ている。
ユーリ「お兄ちゃん! 退屈だよー! なんか楽しいクイズない?」
僕「ユーリ、ひとの部屋に来て、いつもそれ言うよね」
ユーリ「いつも? いま《いつも》って言った? 《いつも》じゃないもん! そーゆーの《誤った一般化》なんだぞー」
僕「はいはい、突っかかるなよ。それだけ退屈してるんだね。クイズか……じゃ、 こういうのはどうだろう」
ユーリ「わくわく」
クイズ
サイコロの置き方は全部で何通りあるか。

ユーリ「$6$ 通り」
僕「え?」
ユーリ「え?」
僕「……」
ユーリ「違うの? だって、サイコロは $6$ 面じゃん?」

僕「ああ、そうかそうか。ごめんごめん。 問題をもっとちゃんというよ。 サイコロの置き方は……うっ、意外に難しいな」
ユーリ「問題出す前に《意外に難しい》とか言わないでよ」
僕「言いたいことはこうなんだ。サイコロを平らな机に置く」
ユーリ「ふんふん。転がらないように」
僕「それで、ええと、サイコロの横の四つの面が、それぞれ東西南北に向かうように置く」
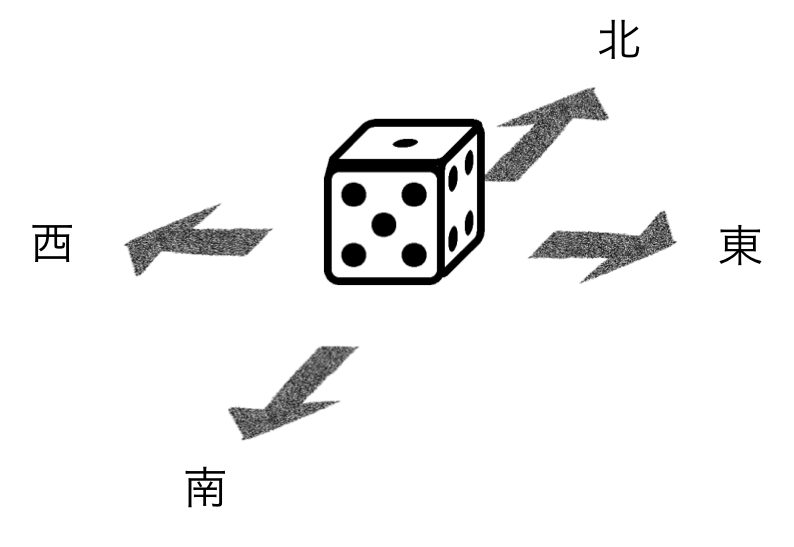
ユーリ「ふんふん。それで呪文を唱えると、召喚獣が現れる」
僕「現れない。サイコロの面は $6$ 面ある。上・下・東・西・南・北にどんな面が向かうかは、 サイコロの置き方で変わる。そこで……サイコロの置き方は全部で何通りあるか」
ユーリ「$24$ 通り」
僕「ユーリ、速いな! 正解!」
ユーリ「へへー。お兄ちゃんが説明している間、考えてたんだもん」
僕「で? どんなふうに考えたんだろう」
ユーリ「どんなふーにって? $6$ 面あって $4$ 通りだから、 $6 \times 4 = 24$ 通りじゃないの?」
僕「いやいや、それは考え方の説明になってないよね」
ユーリ「$24$ 通りでいいんでしょ?」
僕「いいよ。答えはそれでいいんだけど、ユーリがどんなふうに考えたかに興味があるんだ」
ユーリ「頭の中で、サイコロ転がしたの。コロンって転がすと、 $1,2,3,4,5,6$ のどれかが出るよね?」
僕「出るねえ」
ユーリ「だから、最初 $6$ 通りって答えた」
僕「うん、そうだね。その考えは正しいね。《サイコロの置き方は全部で何通りあるか》という問いに対して、 ユーリは上に来る面の種類で答えたわけだ」
サイコロの上に来る面は $6$ 通り

ユーリ「くどく言えばね。 そんで、お兄ちゃんの話で、サイコロを東西南北にきっちり向けるんでしょ。 そうすると、くるくる回すと $4$ 通りあるわけじゃん?」
僕「そうなるね。上面と下面はそのままにして、サイコロを回すと、いつも $4$ 通りある」
サイコロの上面と下面をそのままにして回すと $4$ 通り(図は上面が $1$ で下面が $6$ の例)
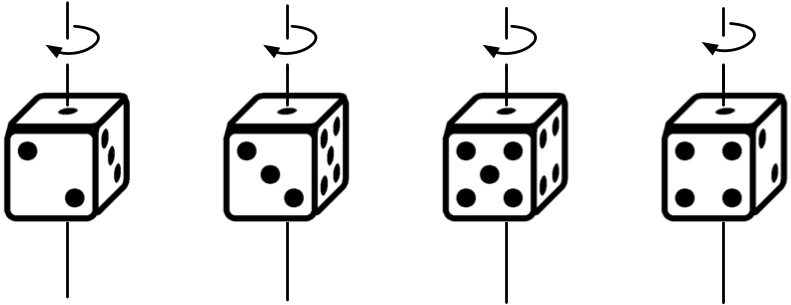
ユーリ「上に来る面が $6$ 通りあって、回すのが $4$ 通りあるから、 $6 \times 4 = 24$ 通り」
僕「いいねえ! ユーリの説明はよくわかったよ」
ユーリ「えへん」
僕「ユーリの説明を聞いていると《確かにそれで正しい》と確信が持てるよ。 それは、《もれなく、だぶりなく》数えているようすがよくわかるから。 そしてそういう話を聞くのは気持ちがいい」
ユーリ「へ? 《もれなく、だぶりなく》ってどーゆーこと?」
僕「意識してなかったんだ。単に答えを出せばいいんじゃなくて、 どんなふうに考えたかを意識するのが大事なんだよ、ユーリ」
ユーリ「はいはい《先生トーク》炸裂だにゃ」
僕「このクイズのように何かの《場合の数》を求めるときには、 《もれなく、だぶりなく》という考え方がとても大事なんだ」
ユーリ「《もれなく》って、もらさないように数えるってこと?」
僕「そうだよ。そして《だぶりなく》というのは、だぶらずに数えるということ。 数えもれがあると少なくなってしまうし、だぶりがあると多くなってしまう。 だから《もれなく、だぶりなく》というのが大事なんだ」
ユーリ「お兄ちゃん、熱く語ってるけど、それって当たり前では? 数えるときに、少なく数えたり、多く数えたりするなー! ちゃんと数えろー! ってことじゃん?」
僕「そうなんだけど、《ちゃんと》数えろだとはっきりしないよね。 《がんばって》数えろとか、《まちがえないように》数えろというのはあいまいだ。 でも《もれなく、だぶりなく》数えろというのは、具体的な方針を示している」
ユーリ「ほほー。にゃるほど。それで? ユーリの $6\times4$ のどこが《もれなく、だぶりなく》なの?」
僕「うん。ユーリはまず《上に来る面は何か》と考えた。 上に来る面は $1,2,3,4,5,6$ の $6$ 通りある」
ユーリ「あたりまえ」
僕「その $6$ 通りで《もれなく》数えているよね。 サイコロの面で $7$ が出たりしないし、 $0$ が出たりしない」
ユーリ「あたりまえの二乗」
僕「それから《だぶりなく》数えてもいる。 サイコロの面で $1$ と $3$ が同時に上に来るということはないから、 $1$ と $3$ は別に数えてかまわないということ」
ユーリ「$1$ と $3$ が同時に上に来たら、もうそれサイコロじゃないし!」
僕「そうだね。だから《上に来る面は何か》と考えて、 $6$ 通りあるというのは《もれなく、だぶりなく》数えている。 そんなふうに確信を持っていえるということになる」
ユーリ「お兄ちゃん、すごいね」
僕「なにが?」
ユーリ「よくそれだけ、当たり前のことをくどくいえるにゃあ……でも、嫌いじゃないぜ」
僕「キャラぶれてるぞ。それから、《上に来る面は何か》を考えた後、 上と下の面は変わらないようにして、サイコロを回したよね」
ユーリ「ふんふん。たとえば $1$ を上にしたままで、東西南北の $4$ 通りに回せる」
僕「そうだよね。それもまた《もれなく、だぶりなく》数えている」
ユーリ「えーと? 《もれなく》ってゆーのは、 東・西・南・北のどこを向くかで全部考えたってことだよね」
僕「そうだね。 $1$ の面を上にしたら、 $2$ の面は必ず側面に来る。側面に来る $2$ は東西南北の $4$ 通りのどれかですべてを尽くしている。 $2$ の面が南東や北北西を向く場合は考えなくていい」
ユーリ「それから、《だぶりなく》ってゆーのは?」
僕「ある面が東を向くと同時に、同じ面が西を向くということがない」
ユーリ「あー、さっきと同じ」
僕「だから横の面が何になるかについても《もれなく、だぶりなく》数えている。 上の面が何になるかを考えて、そのそれぞれに対して横の面が何になるか、《もれなく、だぶりなく》数えたことになる。だから、《正しい》と確信を持っていえる」
ユーリ「めちゃめちゃくどいけど、わかった……ところでお兄ちゃん。 ユーリからもクイズあるんだけど」
僕「お、どんなクイズ?」
ユーリ「いま思いついたんだけど、こんなの」
ユーリのクイズ
サイコロの置き方は $24$ 通りある。
$4$ の階乗 $4!$ は $24$ である。
この謎を解け。召喚獣を呼んでも構わない。
僕「召喚獣こだわるなあ」
ユーリ「そこはスルーしろー!」
僕「なるほど。サイコロの置き方は $24$ 通りで、 $4!$ は $24$ になるね、確かに。 どうしてユーリはそんなことに気付いたんだろう」
ユーリ「$10!$ までは暗記しろって先生言ってたから。 $24$ って $4!$ でしょ?」
$$ \begin{array}{c|rrrrrrrrrr} n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline n! & 1 & 2 & 6 & \FBOX{24} & 120 & 720 & 5040 & 40320 & 362880 & 3628800 \\ \end{array} $$僕「実際、 $$ 4! = 4 \times 3 \times 2 \times 1 = 24 $$ にはなるけど……」
ユーリ「これって偶然? 偶然かもしんない?」
僕「いや、何だか関係がありそうだよ……ちょっと待って、考える」

ユーリ「……」
僕「……」
ユーリ「……わかった?」
僕「……うーん、たぶん。でも納得していない」
ユーリ「納得してないのに、わかったの?」
僕「……うーん」
ユーリ「ほれほれ、何考えているか、お姉さんに話してみ?」
僕「キャラぶれてるぞ。まず《求めるものは何か》と問いかけてみる。 すると、《サイコロの置き方が $4!$ になる理由》を求めていることがわかる」
ユーリ「ふんふん。そだね」
僕「《与えられているものは何か》を考えると、サイコロが与えられている」
ユーリ「ふーん」
僕「《似た問題を知らないか》と考えると、ひらめきがやってきた」
ユーリ「なになに?」
僕「《$4$ 個のものを並べ替える場合の数は $4!$ になる》ということ」
ユーリ「あー、順列だね!」
僕「そういうこと。たとえば $A,B,C,D$ の $4$ 個のものを並べる順列は $4! = 24$ 通りある」
$A,B,C,D$ を並べ替える順列は $4! = 24$ 通り
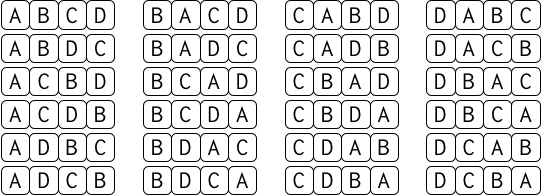
僕「これは重要なひらめきだと思った。なぜなら、 《サイコロの置き方》を《$4$ 個のものの並べ替え》に結びつければいいわけだから」
ユーリ「お兄ちゃん、あったまいいね!」
僕「つまり、サイコロで何か $4$ 個のものを探して、 $A,B,C,D$ と名前を付けて、その順列を見つけ出せばいいんだ……けど」
ユーリ「けど?」
僕「でも、順列では $4$ 個のものの順番を自由に入れ換えられる。 でも、サイコロの場合にはもう形があるんだから、自由に入れ換えられるんだろうか、と思った」
ユーリ「サイコロの $4$ 個のものって何?」
僕「お兄ちゃんが考えたのはサイコロの側面は $4$ 個あるな、と思ったんだけど、 でも順列が作れるほど自由に入れ換えるわけにはいかないね」
ユーリ「あー、そゆこと?面が駄目なら頂点とか辺とか」
僕「サイコロ……立方体の面は $6$ 個で、辺は $12$ 本で、頂点は $8$ 個。どれも $4$ 個じゃないね」
ユーリ「頂点 $8$ 個だったら $2$ で割って $4$ 個にすれば?」
僕「いやいや、そんな勝手に考えてもだめだよ。そもそも頂点は入れ換えたりできないんだから、 順列とは関係がないし……」
ユーリ「そっか」
僕「……いや、待って。頂点は入れ換えられないというのはウソだな」
ユーリ「サイコロゆがんじゃうよ」
僕「サイコロの $8$ 個の頂点のうち、 $4$ 個はいつも机に接している。 机には $4$ 個の場所があって、サイコロの置き方を変えると、机に接する頂点が変わる」
ユーリ「あ?」
僕「もしかして、頂点にうまく名前を付けると、 $4$ 個の順列になるのか?」
ユーリ「待って待って、お兄ちゃん、何いってるかわかんない」
僕「うん。こういうことだよ。机の四箇所に $1,2,3,4$ という番号を付けておく。 ちょうどサイコロの頂点が来る場所にね。そしてサイコロの頂点の方には名前を付けておく。 $A,B,C,D$ のように $4$ 個の名前を付ける」
$4$ 個の場所と、机に接する $4$ 個の頂点
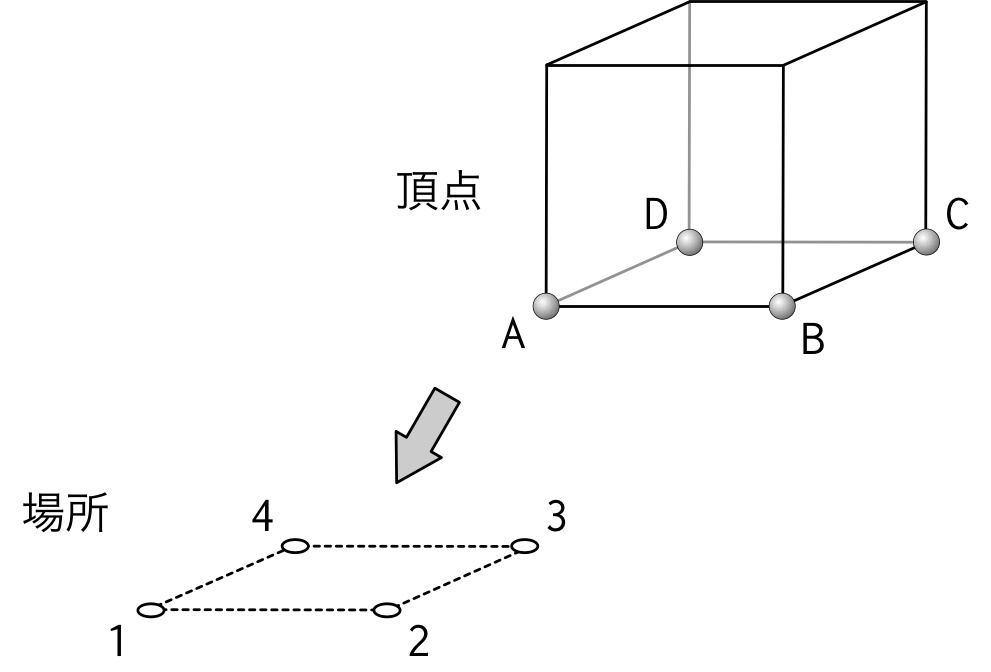
ユーリ「頂点は $8$ 個あるよ?」
僕「だから、同じ名前が付いた頂点を二つ作る。ああ、でも、ややこしくなるから、 $A',B',C',D'$ のようにしたほうがいいかな……おお! うまくいくんじゃないか?」
ユーリ「説明途中で感動しないでよー」
僕「うん。サイコロの置き方は $24$ 通りあるんだけど、 そのそれぞれについて、 机の場所に来る頂点が $A,B,C,D,A',B',C',D'$ から $4$ 個選んだパターンにちょうど合ってるんじゃないかなと思うんだ。 そして $A$ と $A'$ の違いを無視すると、 うまい具合に $4$ 個の順列とサイコロの置き方がぴったり一対一に対応しているはず!と予想」
ユーリ「待って。それおかしいよー。だって、コロンと転がしたら、頂点 $A$ と $A'$ が同時に机に接するかもしんないじゃん!」
僕「ユーリ、それは鋭い指摘だ……おおおおお!」
ユーリ「説明途中で感動しないでってば!」
僕「ユーリのその指摘で、謎が解けたよ。 $A$ と $A'$ が同時に机に接しないようにする方法がある。 $A$ から一番遠い頂点に $A'$ と名前を付けるんだ! $B,C,D$ についても同じようにする。立方体の中心に関して点対称の位置にある頂点に同じ名前を付ければ、 $A$ と $A'$ は同時に机に接することはない!」
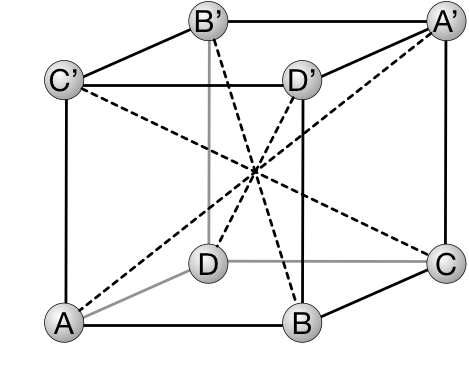
ユーリ「お兄ちゃん、それは《だぶりなく》だね?」
僕「え?」
ユーリ「『どんなふうに考えたかを意識するのは大事なんだよ、かわいいユーリ』って言ってたし。 $A$ と $A'$ が同時に机に接しないように考えるのは《だぶり》が起きないようにするためでしょ?」
僕「確かに……確かにそうだな。待てよ。だとすると《もれなく》の方はどこで押さえるんだろう」
ユーリ「てゆーかさー、たった $24$ 個なんだから、ぜんぶ書こうよー!」
僕「めんどくさがりのユーリから感動的なセリフが!」
そして僕とユーリは協力して $24$ 個のパターンをすべて描き上げた。
机に接する面を決めると、四つの頂点が決まる。 $1,2,3,4$ の場所にどの頂点が来るかを調べる。 そしてそれを回転させる。
机に接する面は $6$ 通りあって、回転させるとそれぞれ $4$ 通りの配置が決まって……
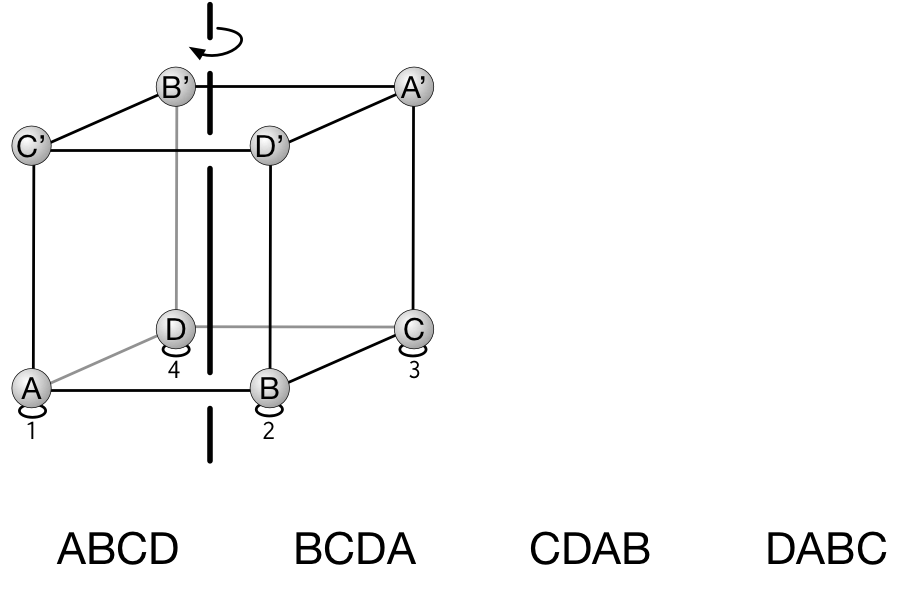
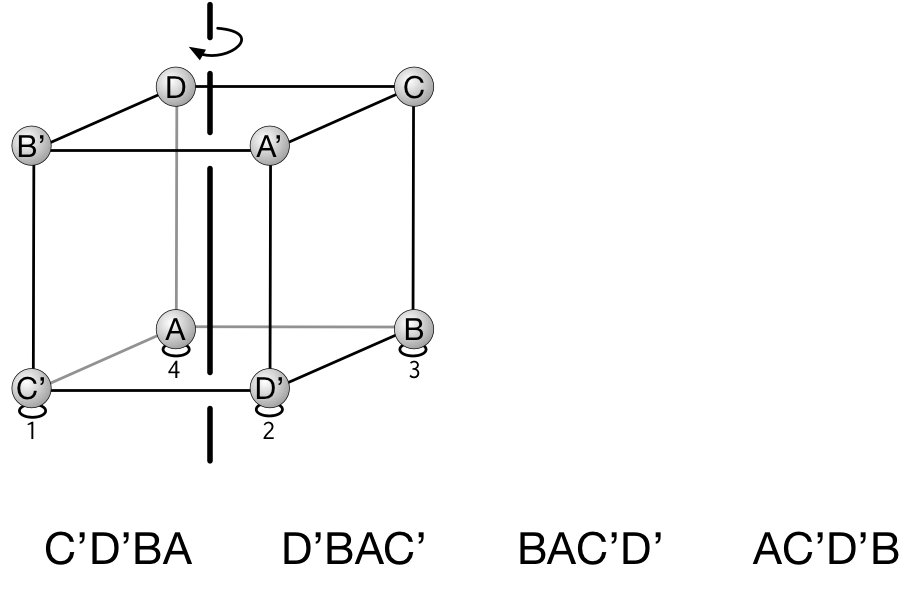
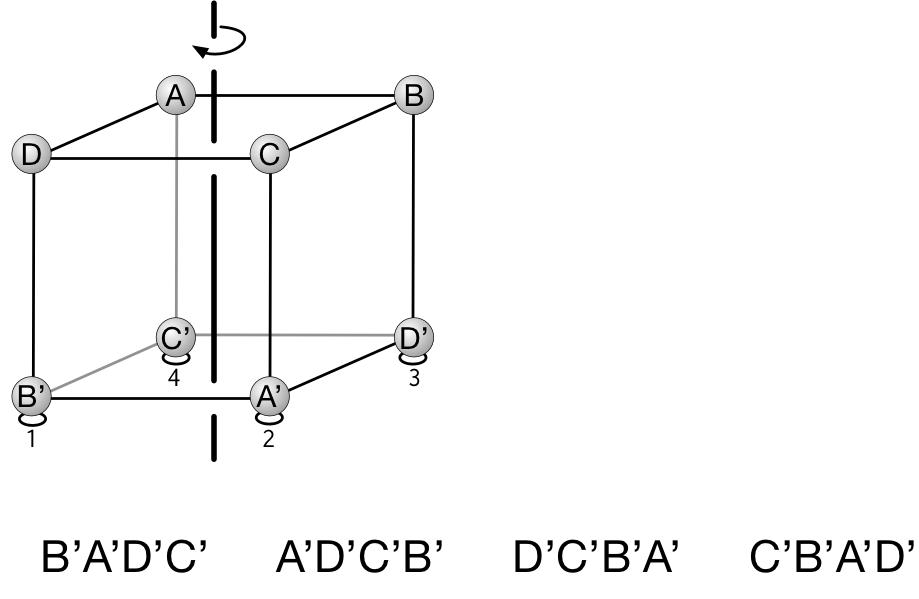
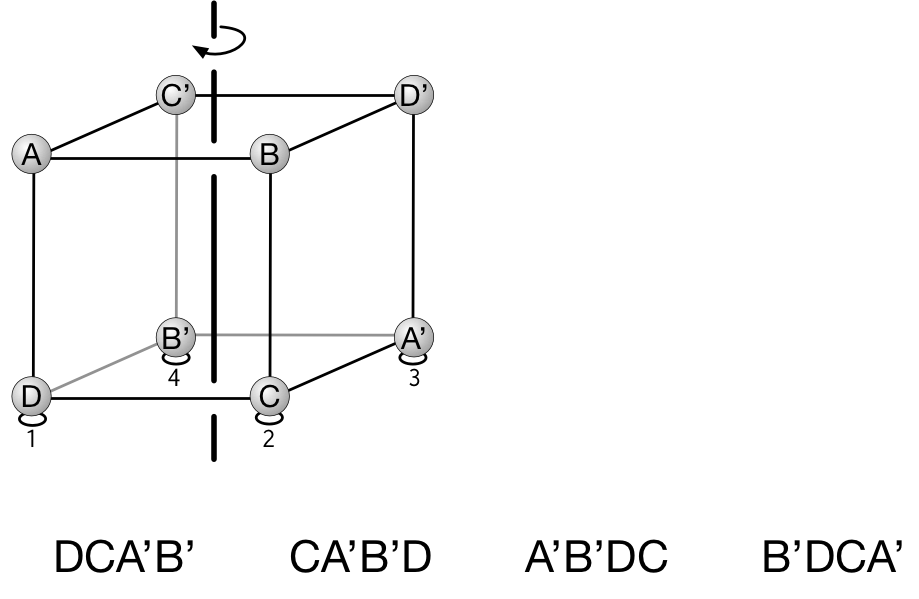
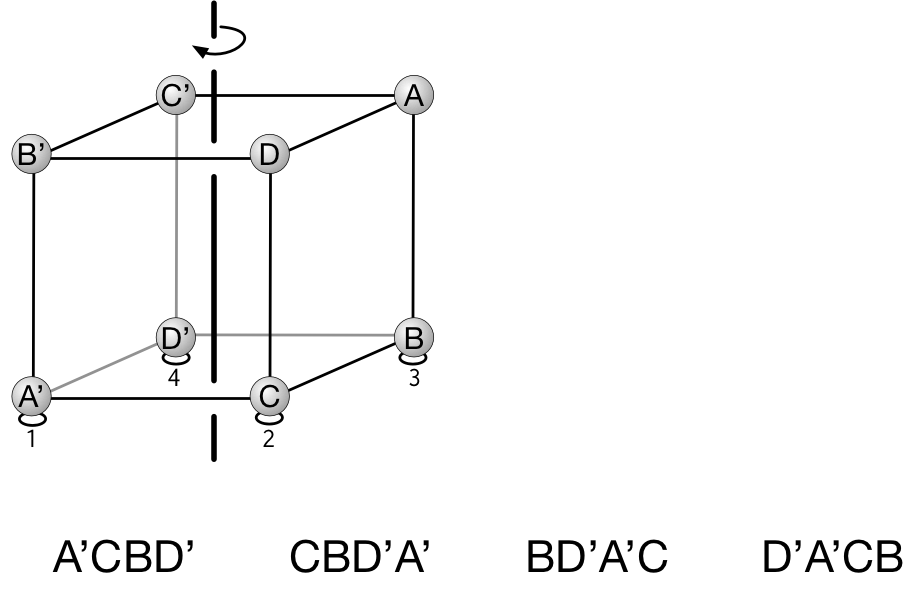
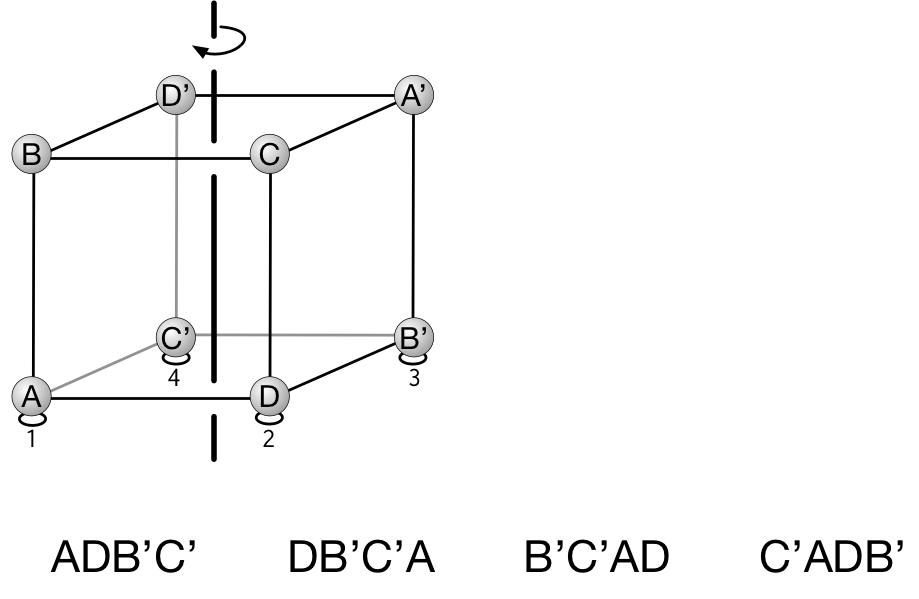
ユーリ「うっわー……うまくいくもんだねー。うまーく、全パターン $24$ 個が出てくる」
僕「そうだね。 $ABCD, BCDA, CDAB, DABC, \ldots$ 確かに、 $\prime$ を無視すると、 $A,B,C,D$ の順列が《もれなく、だぶりなく》でてくるけど……」
ユーリ「けど?」
僕「けど、テトラちゃんのセリフを借りるなら、まだ《わかった感じ》がしないね。 立方体の $8$ 個の頂点に名前を付けて、その置き方をすべて調べたら確かに $4! = 24$ 通りがでてきたけど、 『ああ、確かに順列だなあ!』という感じはしない。 もっとこの $A,B,C,D$ の並びを詳しく研究しないと……」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 420本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第231回終わり)
(2018年8月3日)