![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリ「ちーっす! お兄ちゃん、熱気球って、どーして空飛ぶの? パパッと教えて!」
僕「熱気球?」
ここは僕の部屋。
いつものようにユーリが出し抜けに現れて、 無茶なことを言い出した。
いつものことだけど、どうして必ずパパッと知りたがるんだろうな。
ユーリ「いつものこと、いつものことって、 まるでユーリがお兄ちゃんに『教えて、教えて』って、しょっちゅう言ってるみたいじゃん!」
僕「まさにそうだよね。 お兄ちゃん、お兄ちゃんっていつも言ってる。 てか、地の文にツッコミ禁止」
ユーリ「だって、お兄さまは、いつも教えてくれるじゃん」
僕「お兄さまはやめて」
ユーリは僕のいとこ。すぐ近所に住んでいる。
小さいころから一緒に遊んで来たから、 僕のことはいつも《お兄ちゃん》と呼ぶのだ。
ユーリ「ちなみにここまでのやりとりはテンプレ。 さー、客席も温まって来たところで本題じゃ。 それで? 熱気球って、どーして空飛ぶの?」
熱気球

僕「熱気球が空を飛んでいくのは風に吹かれていくからだと思うんだけど、 たぶんユーリが知りたいのは、そもそも熱気球が空に浮かぶ理由ってことかな?」
ユーリ「もちろんじゃよ」
僕「どうしてユーリは、熱気球の話をポンと出してきたんだろう」
ユーリ「どーしてお兄ちゃんは、熱気球の話をポンと出してくれないんだろう」
僕「いつも言ってるじゃないか。ユーリが熱気球の話を持ち出すきっかけがあるんだったら、 それにそって話したいなと思うからだよ。 何もないところから、『はいっ、それではね。今日は熱気球の話をしていきたいんですけど。 みんなも熱気球って知ってますよね!』と話し出すわけにはいかないよね」
ユーリ「それって、YouTuberのモノマネ? あんましカッコ良くない」
僕「ダメ出しはいいから」
ユーリ「テレビでやってた」
僕「熱気球?」
ユーリ「そだよん。テレビでね、『ものすごい熱の力で、熱気球は空を飛ぶんです!』って言ってたの。 そんで『うみゅ?』って思った」
僕「なるほど?」
ユーリ「熱気球の下にカゴがあるじゃん?」
僕「ゴンドラ」
ユーリ「ゴンドラがあるじゃん? ブワッと火炎放射器で火を出してた」
僕「バーナー」
ユーリ「ブワッとバーナーで火を出してた」
熱気球のゴンドラとバーナー

僕「うん」
ユーリ「確かに熱そうだけど、『熱の力』って何だろ、って思った」
僕「なるほど、なるほど。『熱の力』という言い回しに引っかかったんだ」
ユーリ「お兄ちゃん、《力》の話をしてくれたよね。ニュートンの運動方程式。 あの《力》と『熱の力』って、違うよね?」
僕「違うよ。そのテレビ番組で言ってた『熱の力で熱気球が浮かぶ』というのは、ニュートンの運動方程式に出てくるような、物理学用語としての《力》のことじゃない。 『温めた結果として熱気球が浮かぶ』くらいのごく一般的な意味だと思うよ。 そのテレビ番組で物理学の授業をしていたわけじゃないんだから」
ユーリ「だよねー」
僕「『医者の力で風邪が治った』といっても、加速度が生じたわけじゃない」
ユーリ「ちょっと何言ってるかわかんない。……そんで、話戻るんだけど。熱気球ってどーして空に浮かぶの? 説明できる?」
僕「説明はできると思うよ。 パパッと答えるわけにはいかないけど、一歩ずつなら。 それでもいい?」
ユーリ「いつものことじゃん」
こんなふうにして、僕とユーリの熱気球をめぐるおしゃべりが始まった。
僕「たとえば、熱気球が浮かぶようすを想像する。 最初は地上に静止している熱気球の中の空気をバーナーで温めると、 熱気球は地上を離れて浮かび上がっていく」
地上で静止している熱気球と、空に浮かび上がっていく熱気球
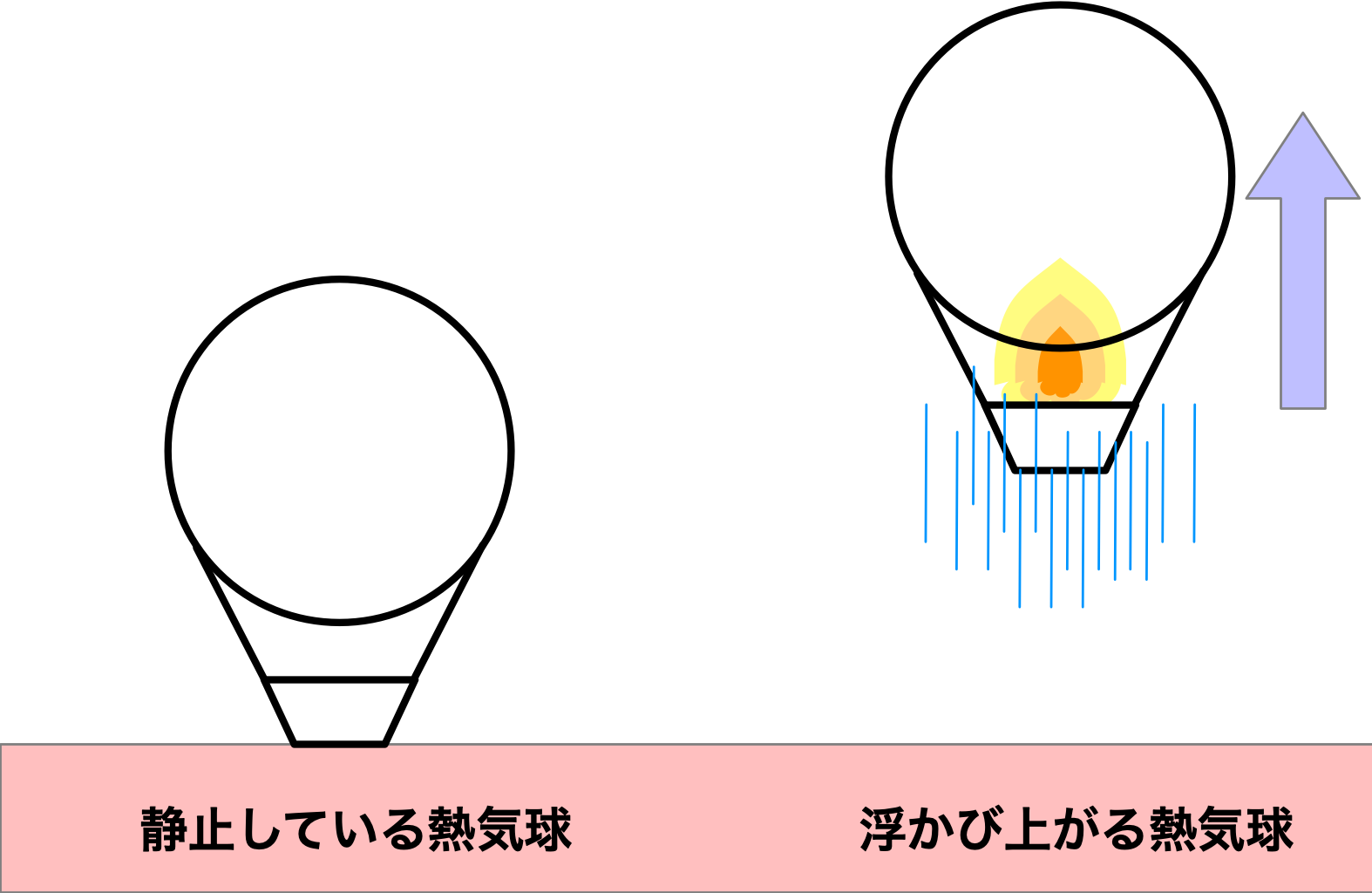
ユーリ「ふむふむ」
僕「静止している状態は速度の大きさがゼロだ。 でも、空に浮かび上がっていくためには、上向きの速度が必要になる。 つまり、この熱気球は上向きに加速度が生じたわけだ。 そして運動の法則によれば、 加速度が生じたということは力が掛かったのだとわかる」
ユーリ「いつも《力》の話になるんじゃのう」
僕「その通りだよ。物体の運動を考えるときには力を考える。 だから、熱気球の運動を考えたいときには、熱気球に掛かるすべての力を考えることになる。 熱気球に掛かるすべての力を足し合わせた合力は、鉛直上向きになっているはず。 なぜかというと、上向きの加速度があるから。そこまではOK?」
ユーリ「オッケー! まず重力があるよね?」
僕「そうだね。 地上から熱気球がまさに浮かび上がるときを考えようか。 そのとき、 地球から熱気球に対して、鉛直下向きの力が掛かっている。 ユーリのいう通り、その力は重力だね。 でもそれだけだと下向きの力だから、下向きに加速度が掛かることになって、静止状態から地面に潜り込んでしまうことになる」
ユーリ「あはははっ! 熱気球じゃなくて熱モグラになっちゃう」
僕「熱気球に上向きの加速度が生じているということから、合力は上向き。だから、下向きの重力だけじゃなくて、上向きの力が何か働いているはずだ」
ユーリ「浮力……だっけ?」
重力と浮力
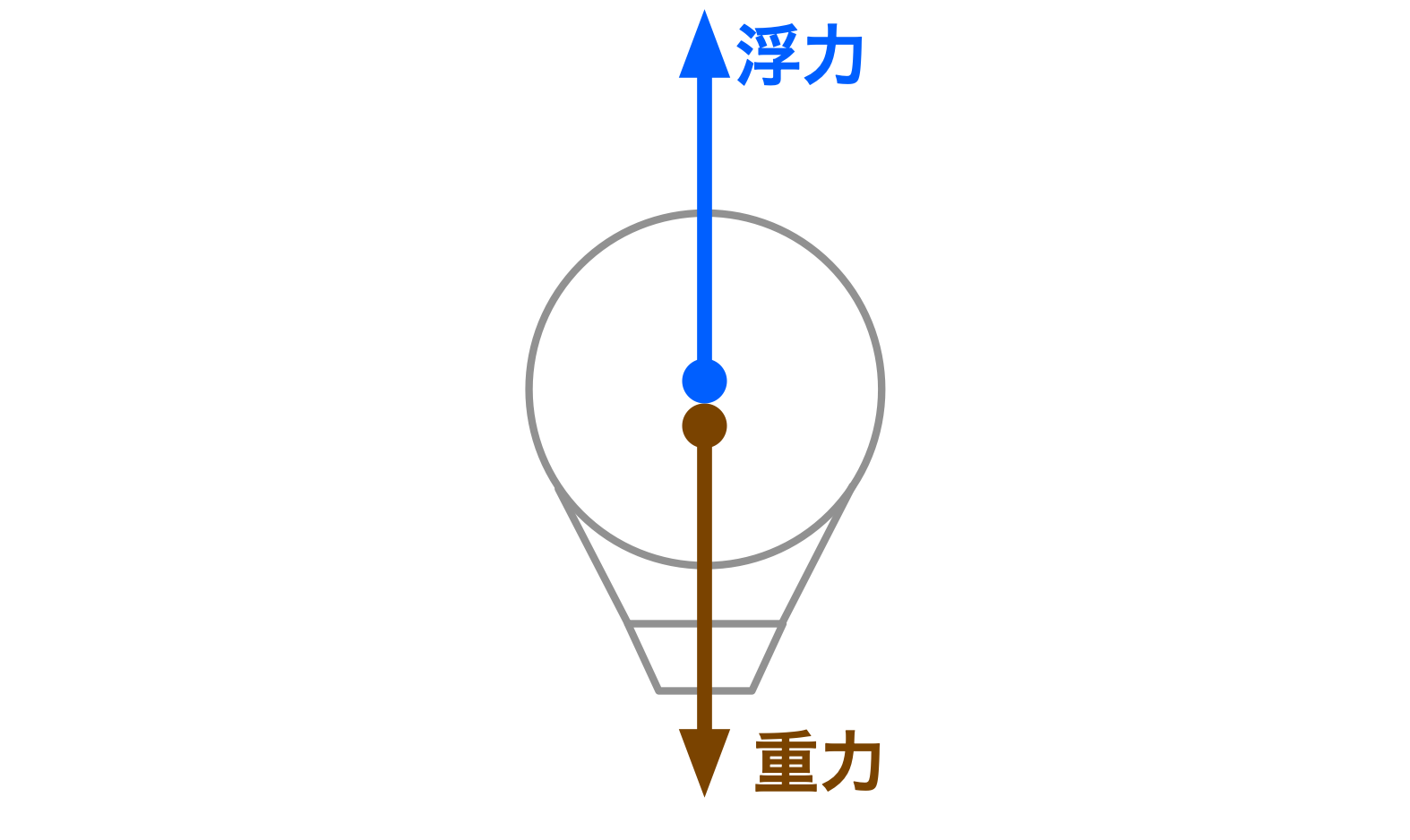
僕「そうだね。浮力(ふりょく)が掛かる」
ユーリ「アルキメデスの原理!」
僕「そうそう。なんだ、ユーリはぜんぶ知ってるんじゃないか」
ユーリ「アルキメデスは、 お風呂に入ってたときにアルキメデスの原理を発見して、 感動して町の中をオールヌードで走り抜けたんでしょ?」
僕「そういう伝説があるみたいだね。ところでアルキメデスの原理の内容は?」
ユーリ「忘れた」
僕「がく」
ユーリ「だって、そのオールヌードで走り抜ける話、インパクトでかすぎるんだもん! 絶対そっちの方を覚えちゃうよね」
僕「それにしても」
ユーリ「お風呂に入ると、ぷかぷか軽くなるから、浮力があることを発見した」
僕「浮力があることだけじゃなくて、どれだけ大きな浮力が掛かるのかが大事。 伝説のポイントは、 お風呂のお湯があふれたところにある。 アルキメデスの原理は、液体や気体の中にある物体に、どれだけ大きな浮力が掛かるのかを教えてくれる物理学的な原理だね」
アルキメデスの原理(液体中の物体が受ける浮力)
液体中にある物体は、上向きの浮力を受ける。
その浮力の大きさは、物体が押しのけた液体の重さに等しい。
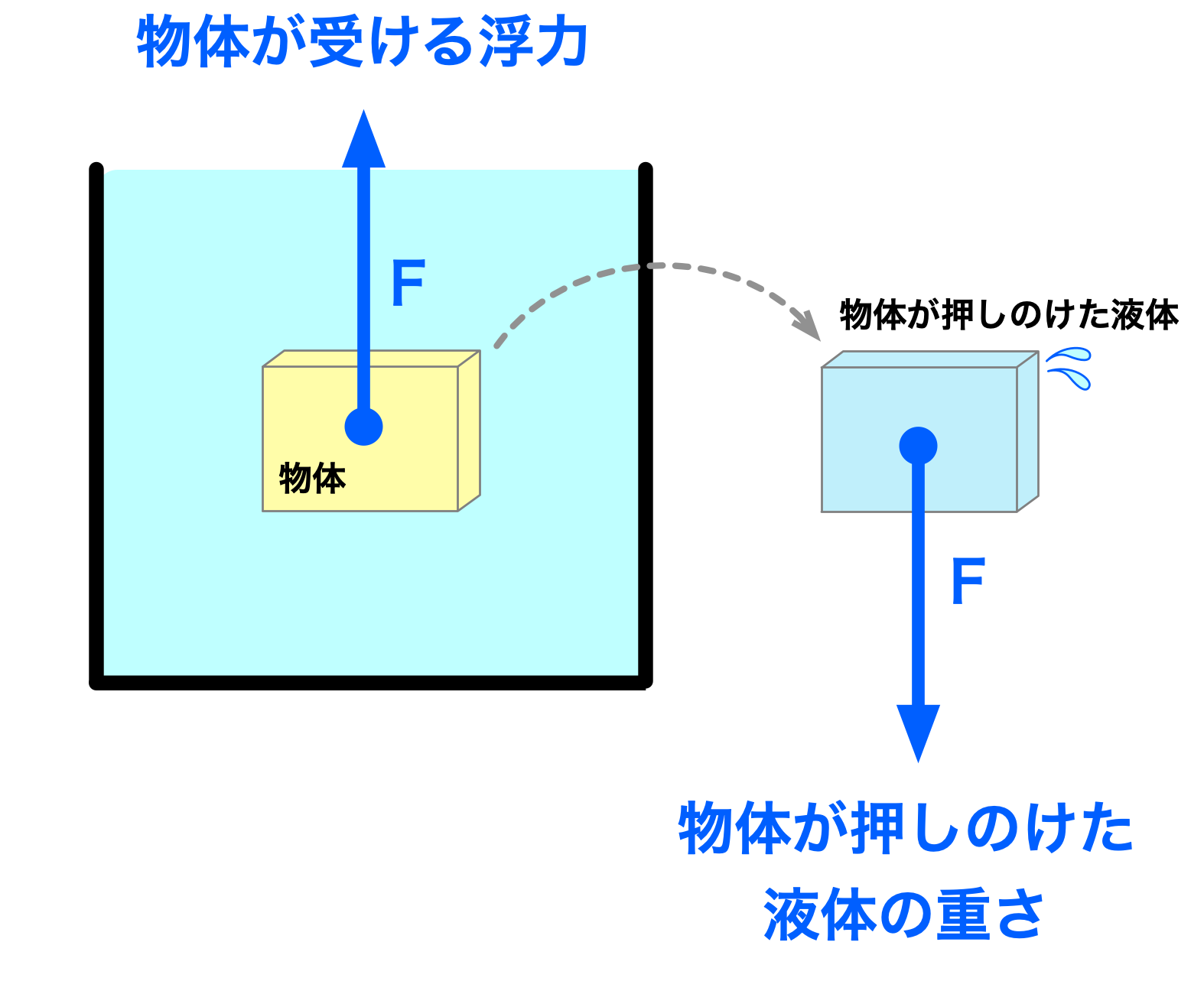
※この図では物体が地球から受ける重力(物体の重さ)は描いていません。
ユーリ「あー、そんな感じで習った習った。 物体が押しのけた液体の重さってわかりにくいよね」
僕「確かにわかりにくいけど、お風呂であふれたお湯の重さだよね。 湯船いっぱいにお湯を満たしておいて、そこにそっと身体を入れると、ざざーっとお湯があふれる。 それは身体がお湯を押しのけたからあふれたわけだ。そのあふれたお湯を一般的には、物体が押しのけた液体と呼んでる」
ユーリ「あっ、お兄ちゃん。 わかりにくいって言ったのは……わかりにくいからだけど、 ユーリもわかってるんだよ」
僕「ユーリがわかっているのはわかってるよ」
ユーリ「ユーリがわかりにくいって思ったのは、 その《アルキメデスの原理》だと、液体に入れる体積で決まるみたいに思えちゃうから」
僕「んん?」
ユーリ「押しのけたお湯の分だけ浮力が働くってことは、 《軽い木の人形》をお風呂に入れても、《重い鉄の人形》をお風呂に入れても同じになっちゃうじゃん? でも、《軽い木の人形》は浮くけど、《重い鉄の人形》は沈むよね?」
僕「待って待って。何か混乱しているぞ。 お風呂の中に二種類の人形を入れた場合を比べるんだよね。 人形が何で出来ていようとも、もしも人形の体積が同じならば、押しのけるお湯の体積は等しい。 だから押しのけたお湯の重さも等しい。だから、アルキメデスの原理によって、確かに浮力の大きさはどちらも等しい。それで正しいよ」
ユーリ「は? だって《重い鉄の人形》は沈むじゃん?」
僕「押しのけたお湯の体積とその重さを調べるのは《浮力》を考えるため。 でも、浮かぶか沈むかを考えるときには《重力と浮力を合わせた合力》を考えている」
ユーリ「お?」
僕「力学ですべての力を書き上げるのは、まさにそういう混乱が起きないようにするためだね。 図に描いてみようか。左が《軽い木の人形》で、右が《重い鉄の人形》だよ。 こんなふうに比べて整理しよう」
ユーリ「……」
僕「わかった?」
ユーリ「わかった。そっか。それだけのことかー。 浮力はどっちも同じだけど、重力が違うんだ。 重い鉄で作った人形の方には大きな重力が掛かっている。 だから浮力と重力を足したときに違いが出る。 浮力は同じ」
僕「そういうこと!」
ユーリ「重力と浮力を分けて考えればよかった」
僕「いまと同じことを熱気球でも考えればいい。 こっちは気体についてのアルキメデスの原理で、浮力を考えるわけだ」
アルキメデスの原理(気体中の物体)
気体中にある物体は、上向きの浮力を受ける。
その浮力の大きさは、物体が押しのけた気体の重さに等しい。
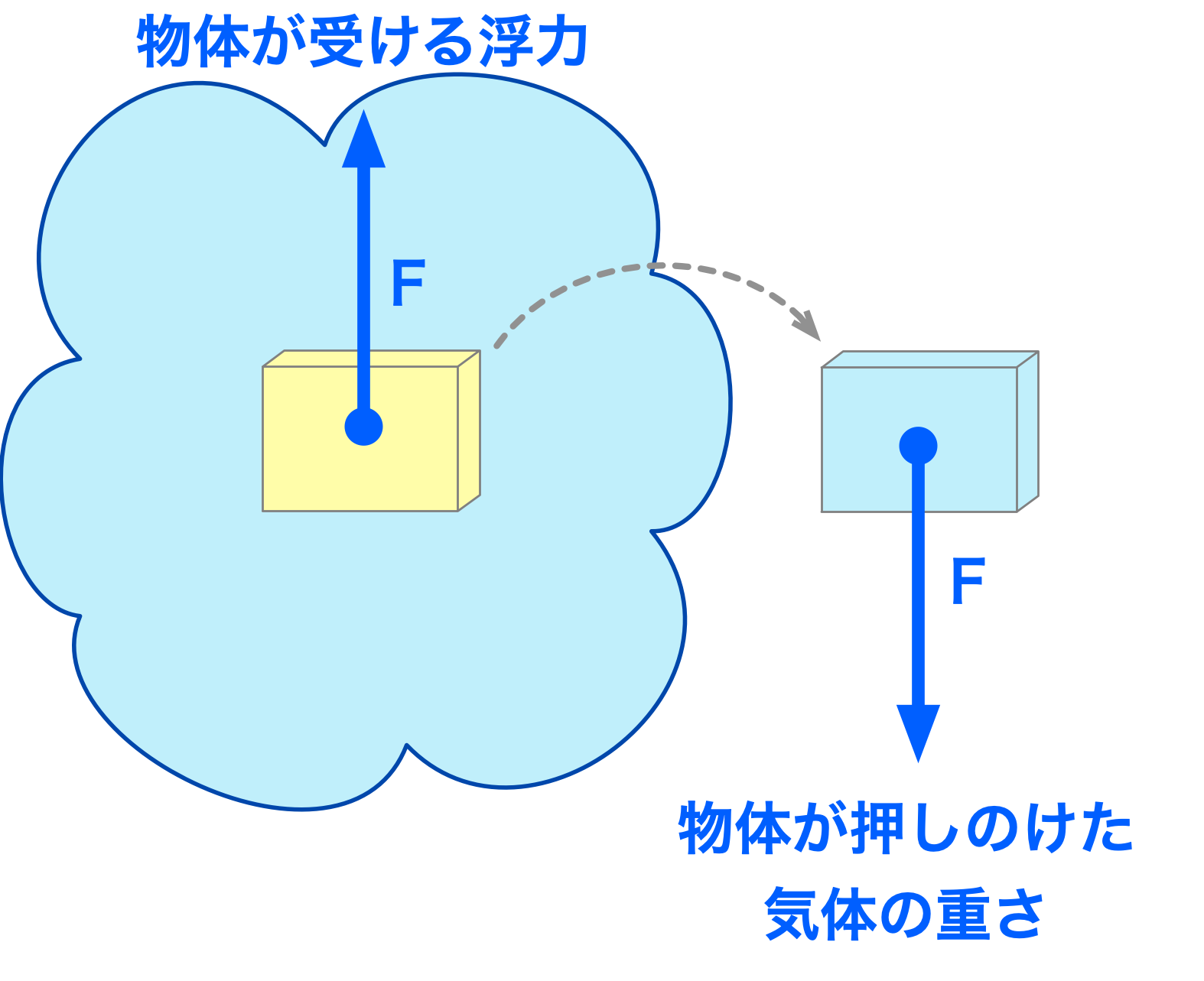
※この図では物体が地球から受ける重力(物体の重さ)は描いていません。
ユーリ「これって、さっきと同じだよね?」
僕「同じだよ。液体を気体に変えただけ」
ユーリ「熱気球って、気体を押しのけてるの?」
僕「そうだね。大気中に存在しているものはみんな気体を押しのけているよ」
ユーリ「それって、空気のことだよね?」
僕「そうだね。空気は窒素や酸素や二酸化炭素などたくさんの気体の混合物だけど、 ともかく気体だ。だから、空気中の物体はアルキメデスの原理で空気から浮力を受ける。 さっきのお風呂に入れた人形と同じように、熱気球は浮力を受けている」
ユーリ「むむ、ってことは、空気中にいる人間は浮力を受けてる? だったら、空気がないところだと人間はもっと重くなる?」
僕「ユーリの考えは正しい。 空気中で体重計に乗るよりも、 真空中で体重計に乗る方が重くなるはず。 ただし、その違いはほんのわずか」
ユーリ「わずか? ……そっか! 押しのけた空気の重さ分しか違わないから!」
僕「そういうことだね。ときどき、 宇宙空間でふわふわ宇宙遊泳できるのを空気が存在しないからだと思う人がいるけど、 それは誤解。浮力という意味では、むしろ空気が存在した方が軽くなる」
ユーリ「熱気球の浮力もアルキメデスの原理?」
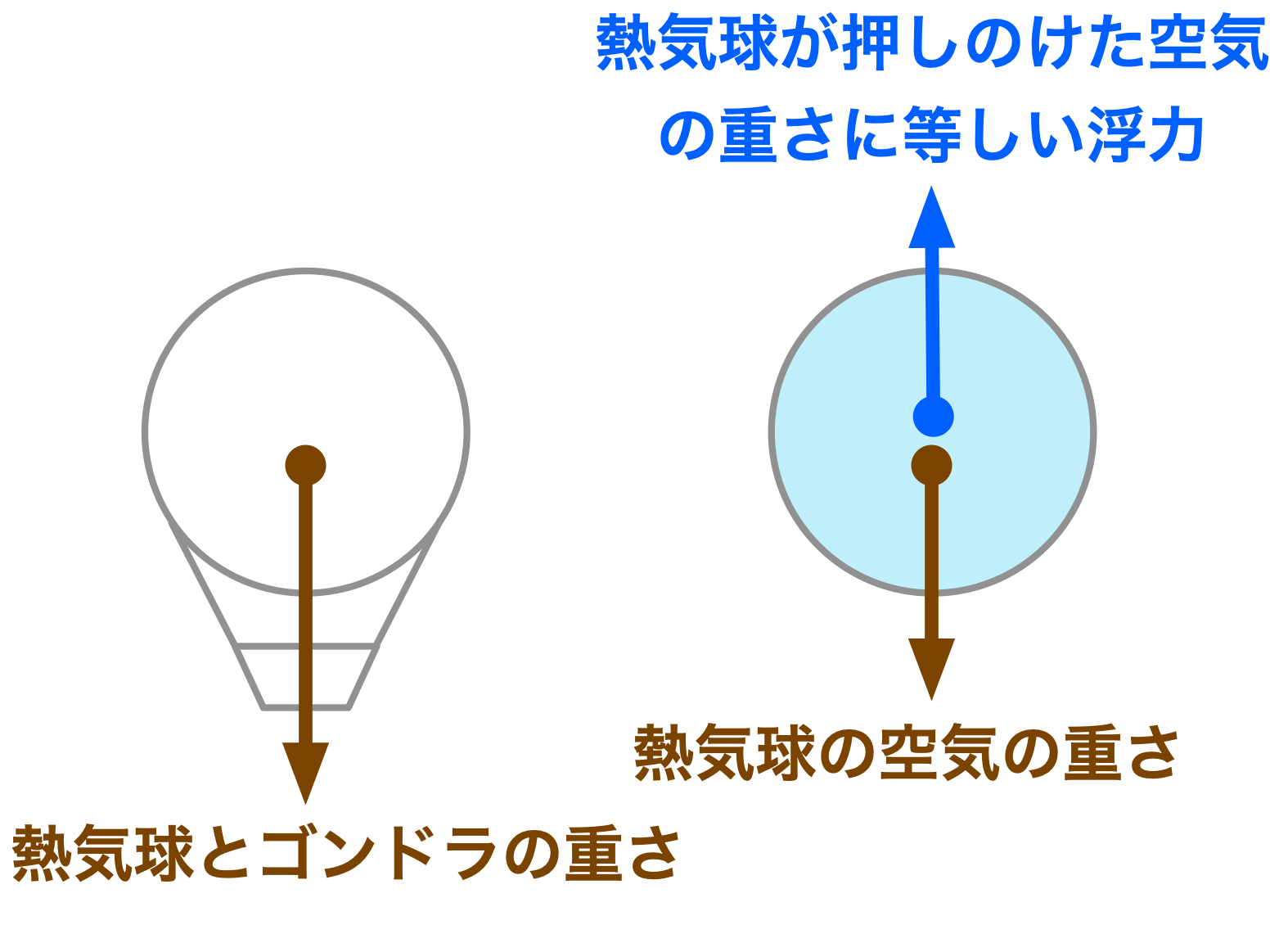
僕「そうだね。地上から浮かび上がる瞬間に熱気球に掛かっている力は二つある」
ユーリ「これを足す」
僕「その通り。 浮かび始める瞬間はちょうど重力と浮力の大きさが等しくなっているときだね。 向きは正反対で、大きさが等しいので、二つの力が釣り合っているときだ。そのときは二つの力を足し合わせた合力はゼロ。 そこから少しでも浮力が大きくなれば、鉛直上向きに加速度が生まれる。そして鉛直上向きに速度が生じて、鉛直上向きに位置が変化していく」
熱気球が浮かび始める瞬間

ユーリ「鉛直上向きに移動していくって《浮かぶ》ってこと!」
僕「そうそう。 重力よりも浮力が大きければ、合力の向きは鉛直上向きになる。 運動の法則から、力の向きには加速度が生じる。 加速度は速度の時間変化だから、 時間が過ぎれば速度は上向きで、大きさは大きくなる。 速度は位置の時間変化だから、 地上で速度ゼロだった熱気球は、鉛直上向きに位置を変えていく」
ユーリ「お兄ちゃんと、
《力》→《加速度》→《速度》→《位置》
の順番に計算したよね! あれだ!」
僕「そうだね」
【CM】
ミルカ「彼とユーリの掛け合い漫才はこちらから。《力》→《加速度》の矢印は、ニュートンの運動方程式からだな」
ミルカ「そして《加速度》→《速度》→《位置》における矢印は、積分だ」
ユーリ「ミルカさまのCMは珍しー」
僕「最近、出番が少ないと嘆いてたから」
ユーリ「メタな発言、自重!」
僕「それはともかく。 熱気球が浮かぶのは《地球からの重力》よりも《空気からの浮力》の方が大きくなるから《浮かぶ》というわけだね。 これがごく簡単な説明になる」
ユーリ「ふーん……」
僕「さっきユーリが、浮力は体積だけで決まると言ってたよね」
ユーリ「うん。アルキメデスの原理」
僕「熱気球をあんなに大きく作る理由がそれでわかる」
ユーリ「浮力を大きくしたいから?」
僕「そういうこと、そういうこと」
ユーリ「ふむふむ。リクツに合ってる! それから、 熱気球は軽く作るよね。それは、重力を小さくするため!」
僕「ナイス。まさにそうだね。じゃあ、ここで簡単なクイズを出すよ」
クイズ
次の(1)から(5)まで話が進むと、熱気球は浮かべなくなる。どこで話がおかしくなっているか?
(1)そもそも、熱気球の中にある気体は空気で、 熱気球が押しのけているのも空気である。
(2)空気が空気を押しのけていることになるから、 《アルキメデスの原理で得られる浮力の大きさ》と、 《熱気球の中にある空気の重さ》は等しいのではないか?
(3)つまり、 《熱気球が押しのけた空気の重さに等しい浮力》と《熱気球の空気の重さ》はちょうど釣り合ってしまう?
(4)ということは、熱気球とゴンドラの重さを考えると、 重力の方が勝ってしまうのではないか?
(5)だとすると、熱気球は浮かべない!
ユーリ「は? いやいや、そんなこたーないよ」
僕「それはなぜ?」
ユーリ「(1)で、空気が空気を押しのけるのはそーだけど、 熱気球の中の空気と外の空気、重さが違うもん。 熱気球の中にある空気の方が軽いでしょ?」
僕「うん、そうだね」
ユーリ「だから、《クイズ》の中で(2)はすでにまちがい! カンタンな話さ!」
僕「では、外の空気よりも熱気球の中にある空気の方が軽いのはなぜ?」
ユーリ「そりゃ、中の空気の方が温かいからじゃん!」
僕「そうだね。温かいから。つまり中の空気の方が温度が高いというわけだ」
ユーリ「お兄ちゃん……《先生トーク》で巧みに誘導してるねえ」
僕「いや、別に誘導してるわけじゃないんだけどな」
ユーリ「またまた」
僕「では、温かい空気の方が軽いのはなぜ?」
ユーリ「そりゃ、温かい空気の方が上に昇るよね。 湯気も上に昇るし、部屋は上の方が暖まるし。 だから対流するんだもん」
僕「うん。ユーリが言ってることは正しい。何もまちがったことは言ってない。でも、それじゃ理由を答えていないよね」
ユーリ「あー、そだね。 えーと……そっか、温かい空気の方が温度が高くて、空気の分子が激しく動くからだ!」
僕「いいね! 温度が高いときに空気の分子が激しく動くというのは正しい。 空気は窒素や酸素や二酸化炭素などの混合物。 気体の状態で空間に存在するときには、小さな粒……分子(ぶんし)になっている。 とても小さくて、目には見えないけどね。 そして温度が高いとき、分子は高速で運動している」
ユーリ「理科で習った」
僕「では、分子が高速で運動している空気の方が軽いのはなぜ?」
ユーリ「なぜ、なぜ、なぜ、なぜ、なぜが続くにゃあ……」
僕「でもこういうの、好きだろ?」
ユーリ「好き」
僕「では、分子が高速で運動している空気の方が軽いのはなぜ?」
ユーリ「うーん……あのね、速く動く方が大きいの」
僕「大きいって、速度が?」
ユーリ「違う。速く動く方が、何だか……広い範囲を動けるって感じがする。 うー……何となくはわかるんだけど、うまく言えにゃい」
僕「もうユーリはほとんど答えているよ。 ある一定の時間を考えると、 分子が高速で運動している空気の方が、空間の中で広い範囲を動き回れるってことだよね?」
ユーリ「だから、そー言ってんじゃん。体積! 大きな体積になる?」
僕「そうだね。分子が高速で運動している空気の方が体積が大きくなる。 単位時間で長い距離を移動するからだね。 そうすると、一定の体積当たりに存在する分子の数が少なくなる。 だから軽くなる」
ユーリ「ちょっと待って……分子の数って少なくなるの? たとえば空気が漏れなかったら、 風船が膨らんでも分子の数は減らないよね?」
空気が漏れなかったら、風船が膨らんでも分子の数は減らない
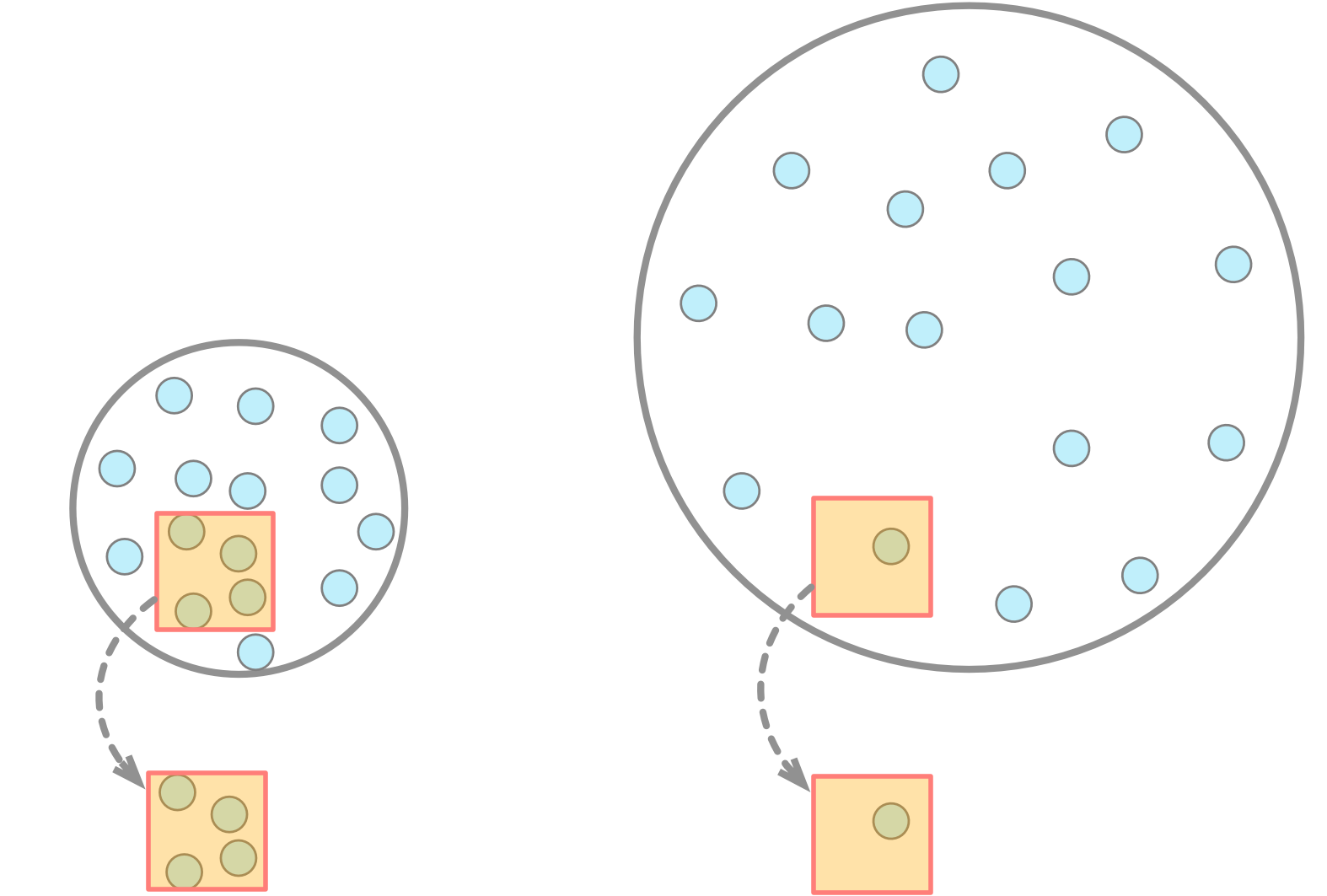
僕「ユーリがいうのは風船の中にある分子の総数だよね。 空気が漏れていなければ、分子の総数は減らないよ。それについてはユーリの言う通り。 さっき僕が少なくなるといったのは、一定の体積当たりに存在する分子の数、つまり密度だよ。 そこをはっきりして考えないとわけがわからなくなる」
空気が漏れなかったら、風船が膨らんでも分子の数は減らない
しかし、一定の体積当たりの分子の数は減る
ユーリ「あっ、わかった」
僕「日本の《人口》と、一定の面積当たりの人口、つまり日本の《人口密度》とはまったく意味が違うよね。 《人口》を面積で割ったものが《人口密度》だから」
ユーリ「わかったって」
僕「熱気球に話を戻そう。熱気球の中の空気を温めると、熱気球の中にある空気は密度が小さくなる。 つまり、単位体積当たりの分子の個数が少なくなる。だから軽くなる」
ユーリ「この差で浮かぶんだね。カンペキに理解した!……あれ、ちょっと待って」
僕「ん?」
ユーリ「熱気球だったらいーけど……」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 420本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第341回終わり)
(2021年12月10日)