![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリ「ねえお兄ちゃん! 極座標で他の図形も描いてみたい!」
僕「なるほど。じゃあね、こんな問題はどう? これは以前、ミルカさんがテトラちゃんに出した問題だよ」
クイズ
次の図形を表す極方程式は $r = \TEXT{《$\theta$の式》}$ という形をしています。 どんな式になるでしょうか。
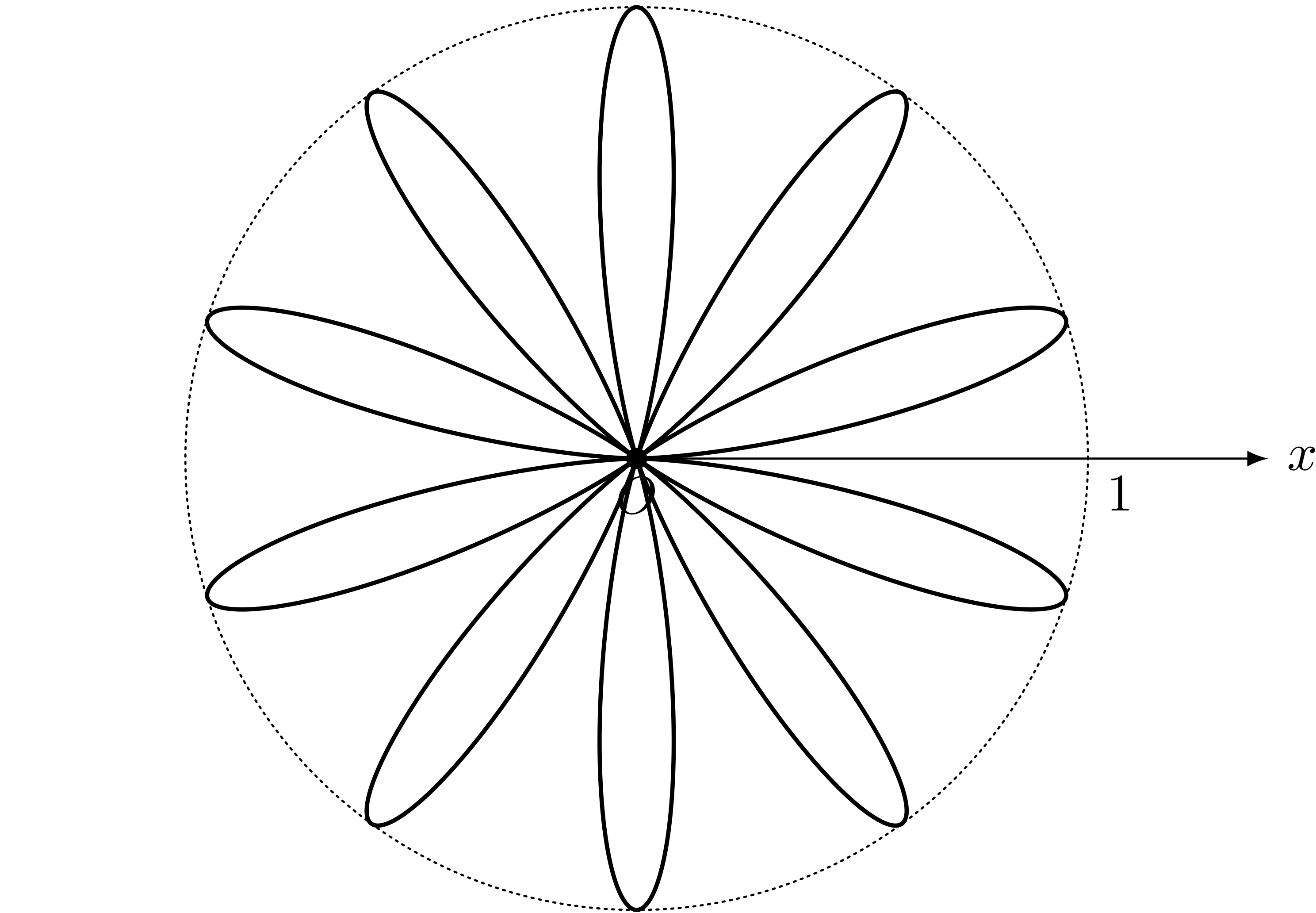
ユーリ「花じゃん!」
僕「まるで花びらのような形だよね。これは螺旋のようにどんどん広がってはいかない形」
ユーリ「《$\theta$ の式》を当てるクイズってことだよね……」
僕「そうだね。式をぴったり当てるのは難しいかもしれないけど、その式がどんな性質を持っているかは当てられると思うよ」
ユーリ「えー……ヒントも手がかりもないのに当てられんの?」
僕「いやいや、目の前にあるこの形、この形自体が、ヒントであり手がかりだよ!」
ユーリ「この形って、ふわ〜っと広がってる。中心からひらひら〜っと広がってる感じするね」
僕「そうだね。でも極座標で考えるときは、そういうふうにとらえるのはまずいよ。まず、この曲線上にある点を一つ決めて……」
ユーリ「ちょっと待ってよ、お兄ちゃん!」
僕「え?」
ユーリ「あのね、『中心からひらひら〜』ってのはユーリの感想なの、か・ん・そ・う。 目の前の花の形を見て感想を言ってるのに、『まずい』とか言うのやめてよね」
僕「おっと……そうだね。ごめんよ」
ユーリ「反省した?」
僕「反省した」
いや、ほんとうに反省した。確かにユーリの言うとおりだ。
僕は答えを知ってるし、考える道筋もわかっている。だからつい、そこから外れると「まずいよ」と言いたくなる。
でも、そんなふうに横から口出されても困るよな。
ユーリ「これって、極 $O$ から始まって、半径が $1$ の円のところまで行ったり来たりしてるよね。 お兄ちゃんが言いたかったのはそーゆーことでしょ? ちゃんとユーリはわかってるんだから。まったくもー」
僕「だからごめんって」
ユーリ「ゆるしたげよう!」
僕「ありがとう!」
ユーリ「それで……この花の形は『花びら』が $10$ 枚ある。 $1,2,3,\ldots,10$ だから、うん、確かに $10$ 枚あるよね」
僕「そうだね」
花びらが $10$ 枚ある
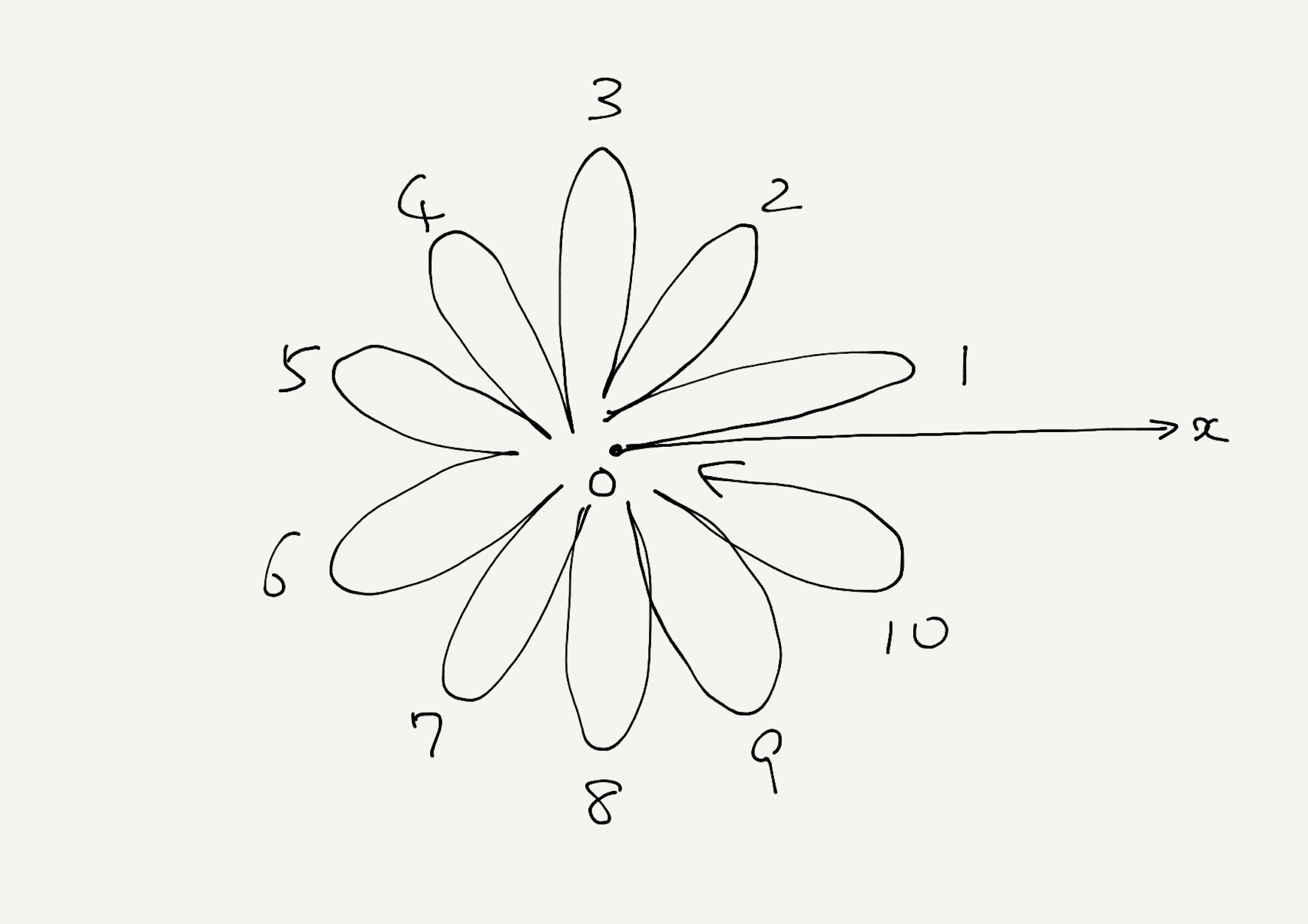
ユーリ「だから、この花の形を描くためには、行ったり来たりを $10$ 回しなきゃ。 $\theta$ がぐるっと $0$ から $360$ まで回るあいだに、 $r$ が大きくなったり小さくなったりするってことじゃん?」
僕「うんうん」
ユーリ「だから、こんなふうにひょいひょいひょい……って $r$ が変化するんじゃね?」
行ったり来たりが $10$ 回あるはず
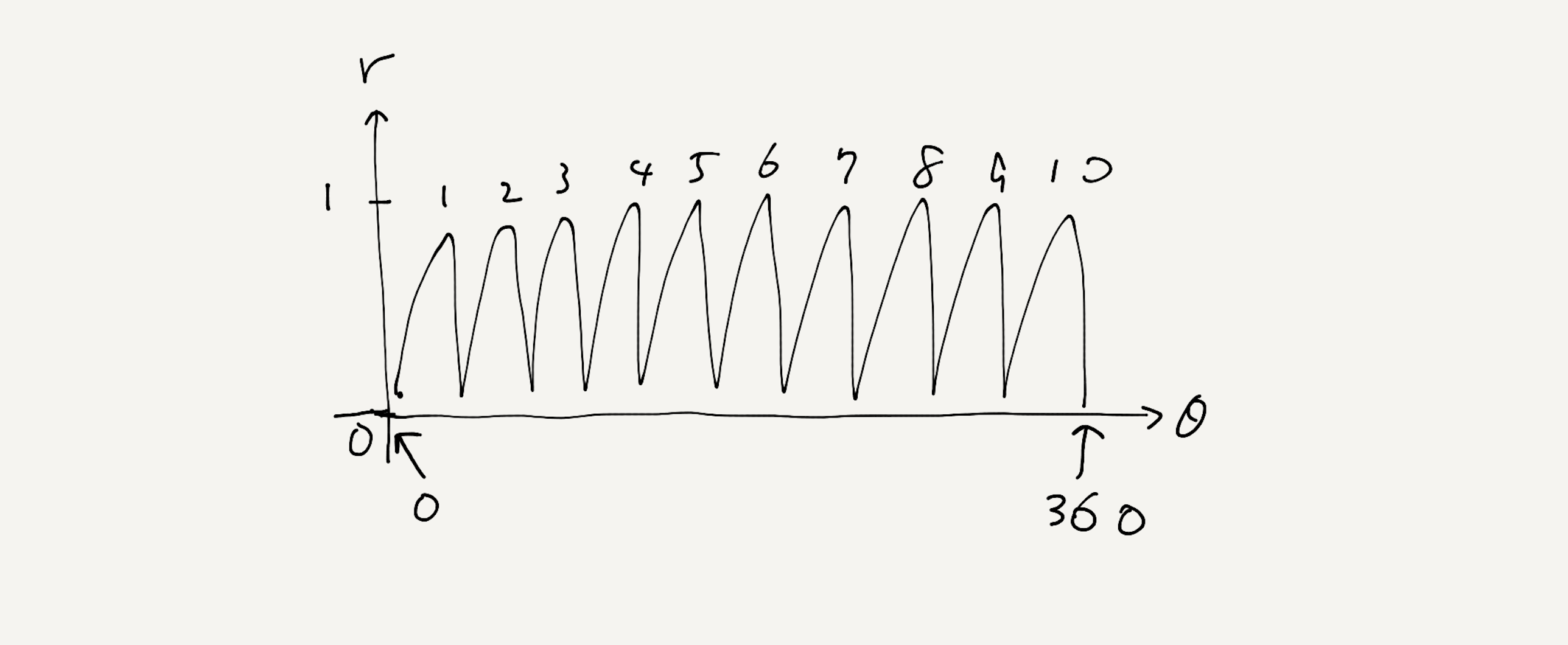
僕「ユーリはちゃんと見てるなあ。 $\theta$ と $r$ の関係を直交座標で表したことになるね。これはうまい!」
ユーリ「でしょでしょ? だから! きっと! サインカーブが出てくるはず!」
僕「おお!」
ユーリ「だってサインカーブだと大きくなったり小さくなったりするもん。ユーリ、わかってんだよ」
僕「ユーリが言ってるのは、 $r = \sin \theta$ を使うってことだよね。横軸を $\theta$ , 縦軸を $r$ にして直交座標でサインカーブを描いてみよう」
$r = \sin\theta$ のグラフ($\theta$ と $r$ を直交座標で表した。 $\theta$ は「度」で考えている)
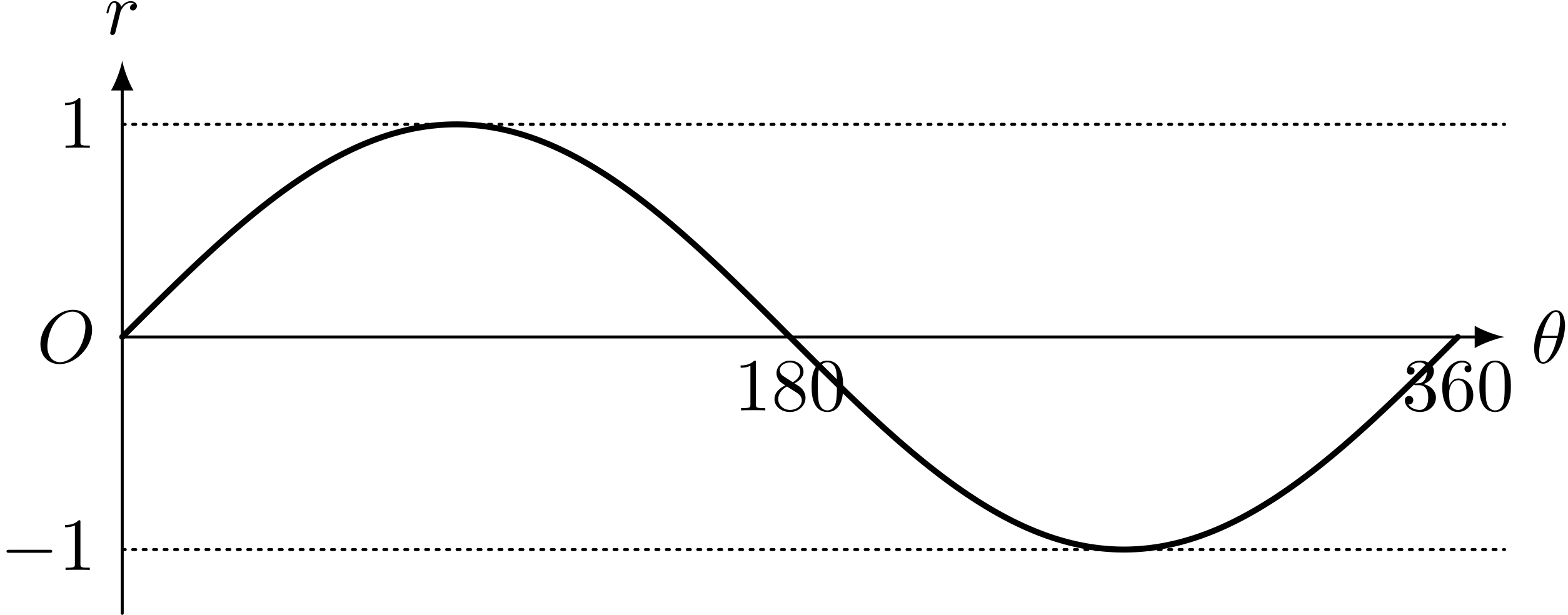
ユーリ「これこれ。あ、だめだ。 $r$ は $0$ と $1$ を往復するんだから、マイナスになっちゃダメ!」
僕「ユーリは、 $r$ の値を $0$ 以上にしたいんだね」
ユーリ「だって動径 $r$ の長さだもん」
僕「《こうなったらいいのになあ》という気持ちが生まれたとき、そこが解決の糸口になるよ」
ユーリ「《先生トーク》炸裂! ……《$0$ 以上になったらいいのにゃあ》……《マイナス部分をぜんぶひっくり返して上に持って来れたらいいのににゃあ》……ってこと?」
サインカーブが《こうなったらいいのににゃあ》
僕「なるほど。ということは、ユーリはマイナス部分の符号を反転したいんだね。つまり、こういうことだ」
$$ r = \begin{cases} \sin\theta && \REMTEXT{($\sin\theta \GEQ 0$の場合)} \\ -\sin\theta && \REMTEXT{($\sin\theta < 0$の場合)} \\ \end{cases} $$ユーリ「それそれ、そーゆーこと」
僕「これは、 $\sin\theta$ の絶対値と呼ばれる計算になるよ」
ユーリ「ぜったいち」
僕「ユーリが言ってた『マイナス部分をぜんぶひっくり返す』というのは……
ユーリ「絶対値、知ってる。縦棒ではさむやつ」
僕「そうだね。『$\heartsuit$ の絶対値』は $\heartsuit$ を $\ABS{\quad}$ ではさんで、 $$ \ABS{\heartsuit} $$ と表す。そしてこの式の値は……
$\heartsuit$ の絶対値 $\ABS{\heartsuit}$
$$ \ABS{\heartsuit} = \begin{cases} \heartsuit && \REMTEXT{($\heartsuit \GEQ 0$の場合)} \\ -\heartsuit && \REMTEXT{($\heartsuit < 0$の場合)} \end{cases} $$
ユーリ「おっけー」
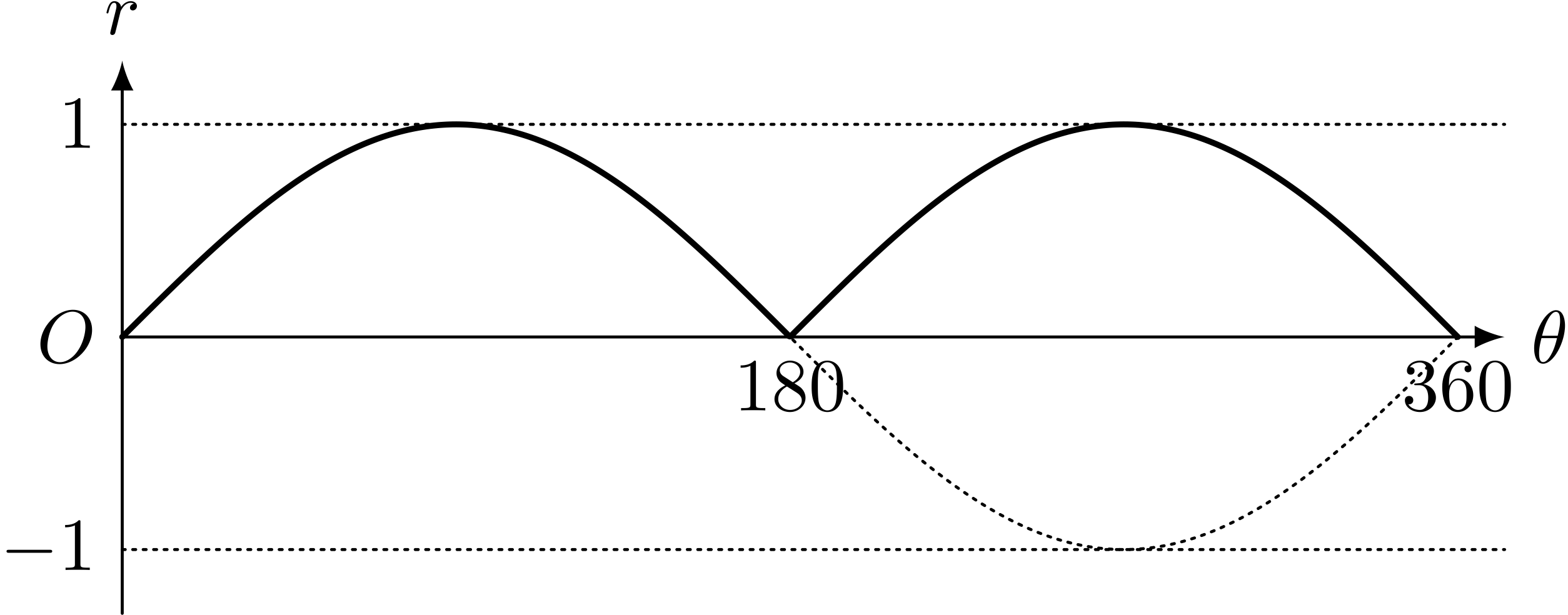
僕「$r = \sin\theta$ と $r = \ABS{\sin\theta}$ をグラフに描いて比較するとこうなる」
$r = \sin\theta$ のグラフ($\theta$ と $r$ を直交座標で表した)

$r = \ABS{\sin\theta}$ のグラフ($\theta$ と $r$ を直交座標で表した)

ユーリ「これこれ! これを使えば花の形になるはず!」
僕「やってみよう。 極方程式 $r = \ABS{\sin\theta}$ を使って描くと……」
極方程式 $r = \ABS{\sin\theta}$ が描く図形
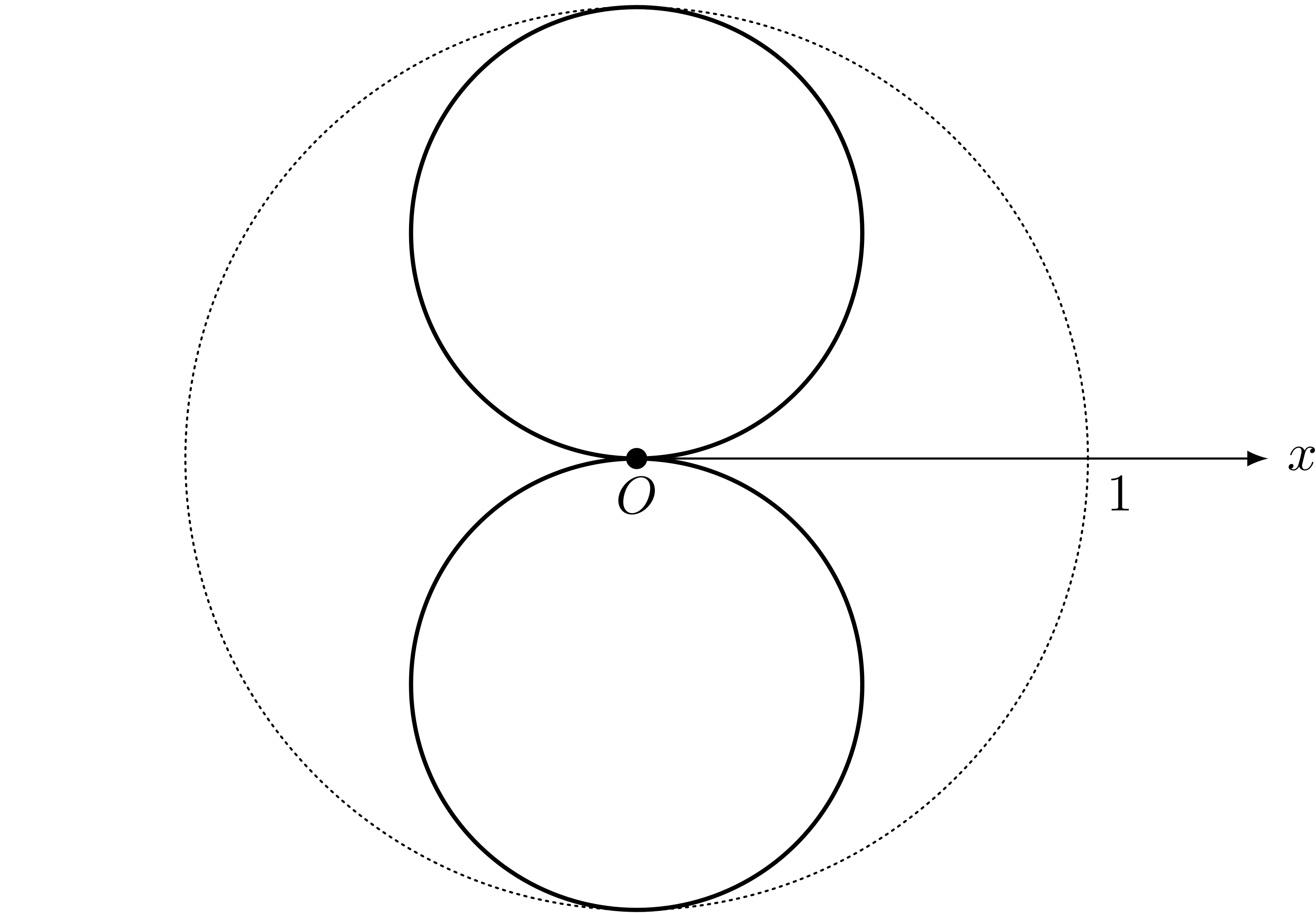
ユーリ「ちがーう! ユーリが言いたかったのは、 $r = \ABS{\sin\theta}$ をそのまま使うんじゃなくて、花びらを $10$ 枚作るってこと! これじゃ $2$ 枚だから、えーと、 $5$ 倍にして、 $$ r = \ABS{\sin5\theta} $$ でやってみてよ」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 420本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2022年7月29日)