![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/場合の数』として書籍化されています。
テトラ「先輩! こちらにいらしたんですね!」
僕「あ、テトラちゃん」
テトラ「ご一緒してもいいですか?」
ここは僕の高校。いまはお昼休み。 屋上でパンを食べていたら、後輩のテトラちゃんがやってきた。 彼女は、僕の隣に腰を下ろす。
僕「僕を探してたの?」
テトラ「え、あ、いえ……そ、そういうわけでもないんですが。 ふと通りかかったもので」
(どうやって屋上にふと通りかかるんだろう……)と僕は考えながらパンをかじる。
僕「もうお昼は食べたの?」
テトラ「え、あ、はい」
僕「今日は気持ちのいい風が吹いてるよね」
テトラ「そうですね」
僕「……テトラちゃん、数学ずっとがんばってるよね」
テトラ「そ、それほどでもないんですけど……あの、先輩?」
僕「なに?」
テトラ「最近よく思うことがあるんです。あの……『考える』ってどういうことなのか」
僕「それはまた……根源的な問いだね。考えるとは何か」
テトラ「あ、え、でも、そんなに難しく考えているわけではなくて、 その……数学の問題を解くときの話なんです」
僕「というと?」
テトラ「あたし……あたしは、あたしなりには数学をがんばってるつもりなんです。 でも、参考書を読んでいると『あたしにはそんなこと思いつかない!』ということがよくあるんです……」
僕「なるほど?」
テトラ「頭の回転がちがうといいますか、なんといいますか……どうしたらそんなこと考えつくのかすら、わからなくて。 どうすればいいんでしょうね」
僕「いやいや、テトラちゃん。僕もそんなに頭の回転が早いわけじゃないよ。 それに僕も『こんなの思いつかないよ』ということはよくあるし」
テトラ「あ、先輩でもそうなんですか!」
僕「そうそう。 解けなくて問題集の解答を読むときって二パターンあるよね。 『すごいなあ』と感心するときと、 『こんなの思いつくわけないし!』とムッと来るとき」
テトラ「そうなんですね。あたしにはその違い、よくわかりませんが……」
僕「なんていうのかな、問題のための問題というか……『他に何にも応用できないよ、こんなこと』 と思う問題は解いててもあまり面白くないよね」
テトラ「えっと、あたしはそんな境地にはまだまだ……あの、たとえば、先輩はこの問題わかります?」
僕「どんな問題?」
テトラ「先日、テレビで中華レストランの店内が放送されてたんです」
僕「うん」
テトラ「Lazy Susanが乗っている丸テーブルがあって……」
僕「レイジースーザンって何?」
テトラ「丸テーブルの上でくるくるまわる回転台です」
僕「へえ……レイジースーザンっていうんだ、あれ」
テトラ「それで、その丸テーブルの周りにお客さんが座りますよね」
僕「うん、そうだね。食事する人」
テトラ「その番組見ながら思ったんですけど、ああいうときって、隣の人とはよく話せるけれど、 遠い人とはあまり話せないじゃないですか。席が決まってて」
僕「うんうん」
テトラ「みんなと話すなら、ときどき席をかえなくちゃいけませんよね。 それでふと思ったんですが、たとえば、 $5$ 人が丸テーブルに座るときの座り方って何通りあるのか……」
僕「なるほど。それはね」
テトラ「先輩! 待ってください!」
問題(中華料理店の問題)
$5$ 個の席が円形に配置されている丸テーブルがあり、 そこに $5$ 人の人が座る。 このとき、着席方法は何通りか。

僕「え?」
テトラ「ちょっと待ってください、先輩。 すぐ答え言わないでくださいよう」
僕「はいはい。テトラちゃんはどんなふうに考えたの?」
テトラ「$5$ 人を並べるんですから、全部書いて数えようと思ったんです」
僕「ほほう」
テトラ「ええと……これです。でも途中で混乱してしまって……」
テトラちゃんはノートを取り出した。
テトラちゃんのノート
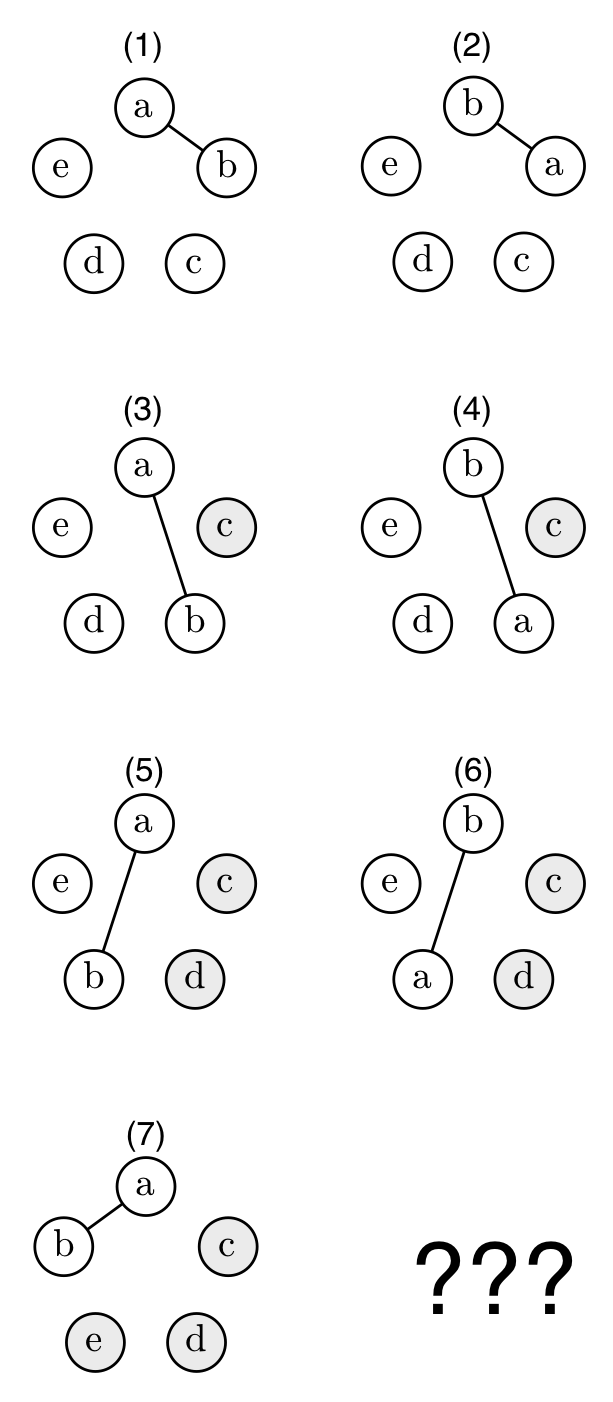
僕「なるほど。テトラちゃんはがんばって数え上げようと思ったんだね。 まあそれは大事な方法の一つだけど」
テトラ「はい」
僕「あれ、でも……これはどういう順番で数え上げようとしたの?」
テトラ「あのですね。aさん、bさん、cさん、dさん、eさんの $5$ 人が座るのだということにして、 書いていこうと思ったんです。まず、右回りにa,b,c,d,eと座ります(1)」
僕「うん。基本だね」
テトラ「aさんとbさんの二人が逆になるときもあると思ったので、aさんとbさんを入れ換えた形も考えました(2)」
僕「お……うん」
テトラ「それから、二人が隣り合うんじゃなくて、 間にcさんがはさまることもあると思いました(3)」
僕「うん、まあね……」
テトラ「そして、先ほどと同じように二人を入れ換えて……(4)」
僕「テトラちゃん……」
テトラ「今度は二人の間にcさんとdさんがはさまる場合を考えて(5)、 そしてまた、二人を入れ換えます(6)」
僕「テトラちゃん、でも……」
テトラ「それでですね、二人の間にc,d,eの三人をはさんだところで(7)、あたしは気づいてしまいました」
僕「……」
テトラ「この並び方(7)は、くるっと回すと(2)と同じなんです!」
テトラちゃんの(7)は(2)と同じ
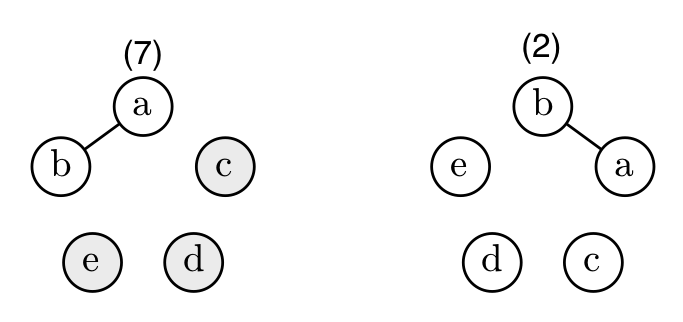
僕「そうなるよね。この数え方はまずいよね。だぶってしまっている」
テトラ「はい……まずいです。 aさんとbさんの二人……その間にはさまれる人の人数を増やしていけばいいと考えていたんですが、 丸いテーブルというのがトラップでしたっ! うっかりすると同じ座り方が出てきてしまうんですっ!」
僕「その通りだね」
テトラ「そこであたし……この問題から離れて考え込んでしまいました。 こういうときに何をどう考えたらいいんでしょう。 どうしたら数学の問題を確実に解くことができるんでしょう」
僕「……うーん、あのね、テトラちゃん。 どんな数学の問題でも確実に解く方法っていうのはないんだよ」
テトラ「あ、それは……それはそうですよね。すみません。 でも、だとしたら、ものすごくたくさんの解法を暗記しなければならなくなりませんか? だって、 数学の問題っていろんなバリエーションがあるじゃないですか。 それなのにその一つ一つのために解き方を覚えるなんて……」
僕「うん、悩んじゃうよね。 たった一つの方法で、数学の問題をすべて解くわけにはいかない。 でも、一つ一つの数学の問題を解く方法すべてを暗記することもできない……」
テトラ「そうです、そうです! 万能の武器もなくて、 たくさんの武器全部を揃えるわけにもいかないなら、いったいどうすればいいんでしょう?」
僕「ねえ、テトラちゃん。テトラちゃんのその考えは極端すぎるんじゃないかなあ。 問題に対する解法を単純化しすぎてるというか。 真実はそのあいだにあると思うな」
テトラ「といいますと」
僕「数学の問題を解くときっていうのは、 自分のこれまでの経験を総動員して解く。 でもそれは、解法を暗記しているというわけじゃないんだよ。 もっと抽象的だよね。 問題を読み解いて、 書かれていることを理解して、 条件を整理して、 自分が記憶していることももちろん使って……ね。 そうやって、解答にたどり着くまで進んでいくことになるんだよ」
テトラ「難しいです……」
僕「暗記することも大事だけど、それをどう使うかを考えることはもっと大事だよ。 以前ミルカさんも言ってた『いかにして問題を解くか』という本にも、 たくさんいい方法が書かれていたけど、 そこに、自分がこれまで問題を解いてきた経験……うまくいった経験や失敗した経験を積み重ねていくしかないよね。 たとえば、僕はよくこんな《問いかけ》をするよ」
テトラ「なるほどです……先輩がいまおっしゃった《問いかけ》というのは、 内容は抽象的ですけれど、具体的ですよね。 問題を直接解くことに比べたら抽象的ですけれど、 自分に話しかけるところは具体的だと思いました」
僕「確かにそうだね! 問題に立ち向かうときには、 こういう《問いかけ》をするといいんだよ。自問自答は考えるときに役立つ方法なんだ」
テトラ「ところで、この中華レストランの問題の場合、 先輩はどう考えていきますか? あの、答え一発!ではなくて、 その考え方、考えの進め方をお聞きしたいんですが」
問題(中華料理店の問題)
$5$ 個の席が円形に配置されている丸テーブルがあり、 そこに $5$ 人の人が座る。 このとき、着席方法は何通りか。

僕「うん。僕だったら、テトラちゃんと同じように《図を描いてみる》と思うよ。 $5$ 人の人が座っている図だよね。そして、そのときにはテトラちゃんと同じようにa,b,c,d,eのように 《名前を付けてみる》と思うな」
テトラ「あたしがやったのと同じように……」
僕「まあ、書き並べる順番はテトラちゃんとは違うかもしれないけどね。 そしていくつか書いているうちに、テトラちゃんと同じことに気づくと思う」
テトラ「あたしと同じこと……」
僕「うん。つまりね、ぐるぐる回るから、うっかりすると同じ座り方が出てきてしまう ということ。 なんだっけ、レイジースーザンに座るわけじゃないから席が実際にぐるぐる回るわけじゃないけど、 席の相対的な位置関係としてぐるぐる回るのと同じことだよね。 うん、ぐるぐる回るから数えにくいということに気づくと思う」
テトラ「はい、そうですよね。数えにくいです」
僕「そこがポイント。《こうだったらいいのになあ》が出てくるときだ」
テトラ「こうだったらいいのになあ……?」
僕「つまりね、《ぐるぐる回らなかったら、いいのになあ》というふうに思うんだね」
テトラ「なるほどです! ……でも、実際には回ります」
僕「ぐるぐる回って困るのはなぜかというと、 《違うパターン》だと思って数えていたのに、ぐるぐる回してみたら《同じパターン》だったとわかるからだね。 だぶって数えてしまうわけだ」
テトラ「そうですね」
僕「《ぐるぐる回らなかったら、いいのになあ》……だったら、 回らないようにしよう! それには、最初から誰か一人を固定してしまえばいい!」
テトラ「あ!!」
僕「誰か一人を決めて固定すれば、ぐるぐる回せなくなる。つまり、同じパターンをすでに数えたかどうか気にせずにすむ」
テトラ「誰か一人を《王様》にするってことですね!」
僕「あはは、そうだね。そうなる。王様か。 一人を王様にして、固定して数えよう。 これで《こうならばいいのになあ》という問いをうまく使ったことになる」
テトラ「なるほどです。 《ぐるぐる回らなかったらいいのになあ》から《一人を王様として固定すればいい》に進むんですか……」
僕「そう。テトラちゃんの描いた図だと、上に来るのがaだったりbだったりふらふら変わっていたよね」
テトラ「そうですね。aさんとbさんを交換しようとしたから……」
僕「だったら、aを王様として固定しちゃえば少し数えやすくなる」
aを固定して考えよう
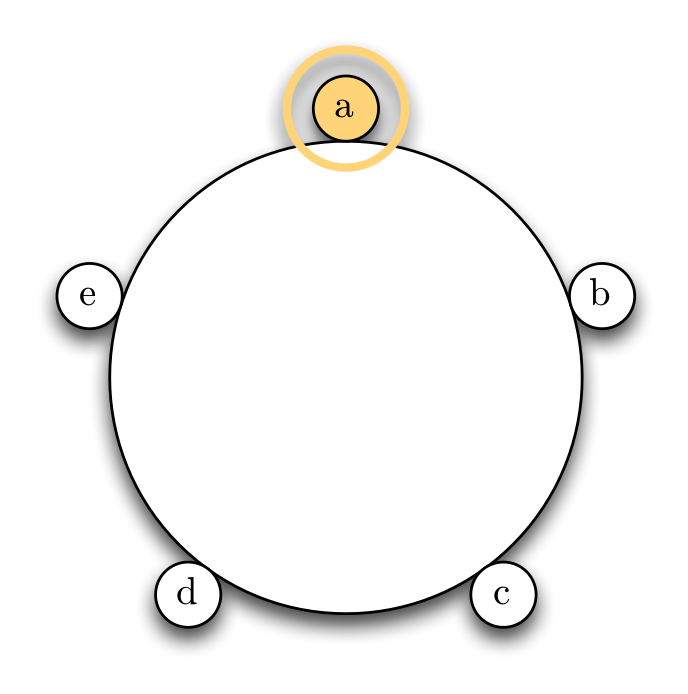
テトラ「なるほどです」
僕「それから《似ている問題を知っているか》という問いかけも使えそうだ」
テトラ「似ている問題?」
僕「僕たちはずっと、円形に人を並べることを考えていたよね。 円形に人を並べる場合の数を考えていた」
テトラ「はい」
僕「円形に並べる方法は知らないけれど、似ている問題は知っているよね。 つまり、一列に並べる問題だ!」
テトラ「……」
僕「実際、よく考えてみると、一人を固定して右回りで考えるってことは、 一列に並べるのと同じことだよね」
テトラ「あ、あれ……ということは、順列ですか?」
僕「そうなるね。円形に人を並べるのは順列として考えられるんだよ。一列に並べる順列は知ってるよね」
テトラ「ちょっと待ってください。でもそれじゃ、《円形に並ぶ》のと《一列に並ぶ》が同じってことになりませんか」
僕「いや、ならないよ。だって、ほら、一人を固定しているから、実際に順番を入れ換えられる人数は $1$ 人減ってる」
テトラ「!!」
僕「円形に人を5人並べるというのは、aを固定しておいて、残りの4人を一列に並べればいいんだね」
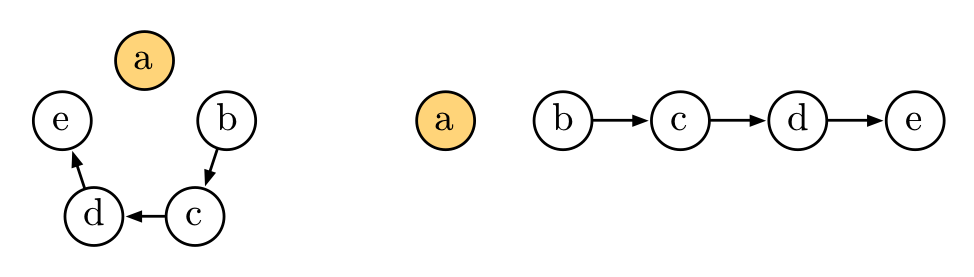
テトラ「ですね!」
僕「aを固定しておいて、右回りに誰を座らせるかを考えよう。 aの次に座れるのは残っている4人。 そのそれぞれに対して、さらに次に座れるのは3人。 そのそれぞれに対して、さらに次に座れるのは2人。 そして最後の席に座れるのは最後に残った1人」
テトラ「確かに、確かに、確かにそうです!」
僕「これでもう解けた。 $5$ 人の人を円形に並べる並べ方の数は、 一人を固定しておいて、残りの $4$ 人を一列に並べる並べ方、すなわち順列の数に等しい。 それは $4! = 4 \times 3 \times 2 \times 1$ で計算できる。 答えは $24$ 通りだね」
解答(中華料理店の問題)
$5$ 個の席が円形に配置されている丸テーブルがあり、 そこに $5$ 人の人が座る。 このとき着席方法は、 $$ 4! = 4 \times 3 \times 2 \times 1 = 24 $$ 通りある。
($1$ 人を固定しておき、残りの $4$ 人を一列に並べる順列として考える)

テトラ「え……先輩、この $24$ 通りの並べ方は?」
僕「ああ、ごめんごめん。頭の中で樹形図(じゅけいず)を描いていたんだよ」
テトラ「?」
僕「こういう図だね」
樹形図
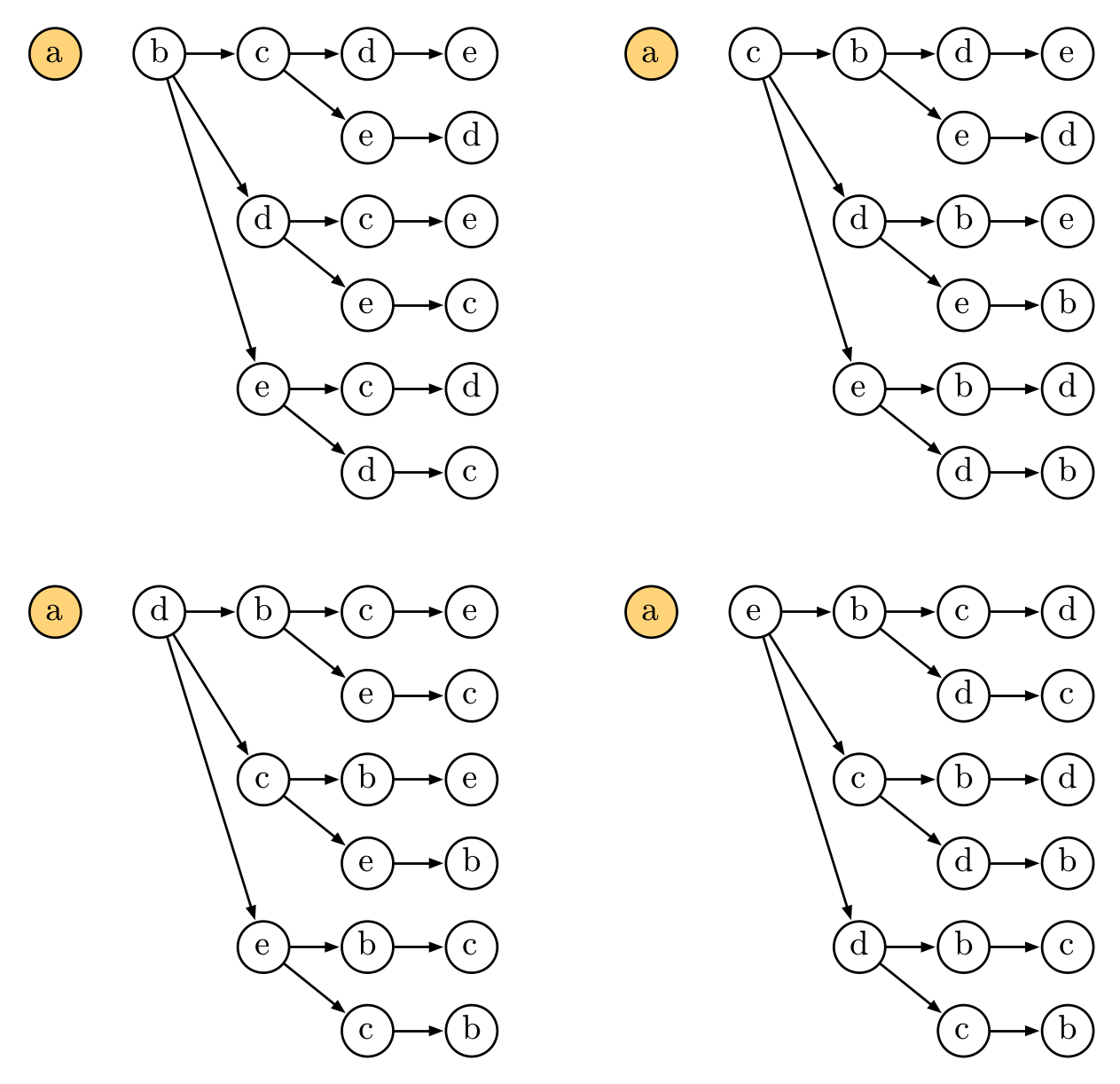
テトラ「ははあ……」
僕「樹形図は《もれなく、だぶりなく》考えるときに便利だよね」
テトラ「そうですね」
僕「それでね、テトラちゃん。ここまでじっくり考えたら、 一般化することは簡単だよね」
テトラ「一般化といいますと」
僕「つまり、 $n$ 人の人を円形に並べる並べ方の個数を求めるということ」
テトラ「$n$ 人……あ、簡単です! 同じように考えればいいんですから。 $n$ 人のうち一人を固定して、残りの $n-1$ 人を一列に 並べます!」
僕「そうだね」
テトラ「だから、 $(n-1)\times (n-2) \times \cdots \times 2 \times 1$ 通りになりますね!」
僕「うん、そうそう。 $(n-1)!$ 通り。これが円順列(えんじゅんれつ)の個数」
円順列の個数
$n$ 人の人を円形に並べる並べ方は、 $$ (n-1)! $$ 通りある。
テトラ「円順列……名前があるんですね!」
僕「うん、最初に言おうと思ったんだけど、テトラちゃんに答えを封じられたから言えなかった」
テトラ「あ……すみません」
僕「この円順列、もう少し考えてみようか。あのね……」
(第62回へ続きます)
テトラ「それでは、恒例の《読者さんへの宿題》コーナーですっ!」
僕「いつから恒例になったのか……」
テトラ「こちらが問題です!」
読者さんへの宿題
$5$ 個の異なる宝石を使って輪にし、ブレスレットを作ります。 何種類のブレスレットが作れるでしょうか。
僕「なるほど。これはね」
テトラ「先輩! 宿題なんですからすぐ答えをいわないでくださいよう!」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 420本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第61回終わり)
(2014年1月10日)
この記事は『数学ガールの秘密ノート/場合の数』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!