![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの物理ノート/波の重ね合わせ』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだけれど飽きっぽい。
ここは僕の部屋。
勉強していると、いとこのユーリが遊びにやってきた。
ユーリ「ちーっす! ……あれ? お兄ちゃん、めずらしく勉強してる」
僕「めずらしくはないよ。まじめな高校生だからね」
ユーリ「だって、ユーリといるとき、いつも遊んでるじゃん」
僕「それは、ユーリが『ねー、お兄ちゃん、 何かおもしろい話ないの? あそぼーよー!』って言うからだろ」
ユーリ「冷たいにゃ……それはさておき、何かおもしろい話ないの?」
僕「さておくなよ。ただいま勉強中!」
ユーリ「ちぇっ……まじめな高校生は何を勉強しておるのかな?」
僕「いまは物理。波動の復習」
ユーリ「ハドーって何?」
僕「波動っていうのは、波のことだよ」
ユーリ「なみ? 波って物理なの?」
僕「そうだね。物理にはいろんな分野があるけれど、 波……波動はその一つになるよ。ユーリも理科で習っただろう?」
ユーリ「習ったっけ」
僕「絶対習ってるよ。たとえば、音のこと習っただろう?」
ユーリ「そっか。音は波か……」
僕「そうだよ。音も波として伝わっていく。だから遠くまで届く」
ユーリ「あ、思い出してきたよ。こんなのだよね」
僕「そういえば、 ユーリはサインカーブを知ってるじゃないか(『数学ガールの秘密ノート/丸い三角関数』参照)。 あれも波だよ」
ユーリ「サインカーブって、あれは数学でしょ?」
僕「数学を使うと、物理的な現象をうまく表せるからね」
ユーリ「結局、波って物理なの? 数学なの?」
僕「ええとね……よし、わかった。 じゃあ、基本的なところから話をしよう。 でないと、ごちゃごちゃしちゃうからね」
ユーリ「たのむぞよ」
僕「物理の話。とっても基本的なところから始めよう。 ユーリは《波》というと、どんなものを思い浮かべる?」
ユーリ「うーんと、海?」
僕「海の波だね。いいよ」
ユーリ「プールの波も」
僕「うんうん。プールにも波がある。それはどちらも水が揺れているわけだね」
ユーリ「他には……地震も波じゃなかったっけ。テレビで見たことある。地震波」
僕「すごいのが来たな。そうだね。あれは地面が揺れている」
ユーリ「あと、さっきお兄ちゃんが言ってた、音も?」
僕「そうそう。あれは空気が揺れている。 だから、空気がない宇宙では音が届かない。 宇宙で爆発が起きても音は聞こえないんだ」
ユーリ「スター・ウォーズではすごい音してたけど」
僕「時事ネタ自重。あれは映画だから……無音だったら悲しいし」
ユーリ「そだね」
僕「いまユーリが言ったのは代表的な波の例だね。 海の波、地震の波、音の波。では、ユーリにクイズだよ。 『波』というのはいったい何だろう」
ユーリ「何だろうって?」
僕「つまり、波の定義は何かということ。 いまから、波について考えようとしているわけだから、 波をきちんと定義しておきたい。波とは何か?」
ユーリ「波の定義……そんなの、考えたことない! だって、波は……波じゃん。見ればわかるし」
僕「ユーリには音が見えるの?」
ユーリ「うっ。見えにゃい……波の定義って何?」
僕「降参?」
ユーリ「降参じゃなくて、戦略的撤退」
僕「何だそれ。じゃあね、 きっちり言えなくていいから、 『波というものには、こういう特徴がある』というものを挙げてごらんよ」
ユーリ「揺れている、とか?」
僕「そうだね。波というからにはともかく揺れていてほしいよね。 つまり、波というのは振動に関係しているわけだ」
ユーリ「ふむふむ」
僕「ところで『振動している』というからには、何かが振動する必要があるよね」
ユーリ「海の水とか?」
僕「そうそう。海やプールの波では、振動しているのは水だし、 地震の波では振動しているのは地面だし、 音の波では振動しているのは空気になる。 ここでいう水や地面や空気のようなもののことを 媒質(ばいしつ)というんだよ」
ユーリ「ばいしつ」
僕「媒質が振動していることの他に、波の特徴は何かある?」
ユーリ「ないよ」
僕「え?」
ユーリ「だって、水が振動したら、もう波ができちゃうじゃん。 他の特徴といわれましても」
僕「じゃあ、これも波?」
僕はそういって、指を上下に振ってみせる。
ユーリ「なにしてんの?」
僕「指を振動させてるんだよ。これも波?」
ユーリ「そんなの、波じゃない。うーん……もっと、波は遠くまで行く!」
僕「いい感じ。 海の波も、地震の波も、音の波も、遠くまで伝わるんだ。 それは、波の大事な特徴だね。 だから、物理で研究する波というのは、こんなふうに定義できるよ」
波の定義
振動が伝わっていく現象を波と呼ぶ。
ユーリ「ふむふむ」
僕「《振動が伝わっていく現象》を波と呼ぶ。 そして、振動が物質を通して伝わるとき、波を伝える物質のことを媒質と呼ぶ」
ユーリ「ねえ、お兄ちゃん。 熱心に先生トークしてるとこ悪いんだけどさ…… 《振動が伝わっていく現象》って、あたりまえのこと言ってるよね」
僕「そうなんだけど、こういう定義を見たときには『何であるか』だけじゃなく、 『何でないか』を考えるといいんだよ。そうすると、定義でいいたい重要なポイントがわかるから」
ユーリ「意味わかんない」
僕「つまり、《振動が伝わっていく現象》を波と呼ぶとしたら、 《振動じゃないものが伝わる現象》は波とは呼ばない、ということ」
ユーリ「おお? ……って、もっと意味わかんない!」
僕「たとえば、お兄ちゃんがユーリにボールをぽんと投げたとする。 キャッチボールだ。 このとき、ボールが伝わったわけだけれど、これは波とは呼ばない」
ユーリ「まー、そーだけど……それ、大事なこと?」
僕「大事なこと。つまりね、 波というのはあくまで振動が遠くまで伝わるのであって、 物質が遠くまで移動しているわけじゃないよ、ということ」
ユーリ「……」
僕「わかる?」
ユーリ「考えてるの」
僕「……」
ユーリ「ねえ、お兄ちゃん! 海の波って、海の水が動くんじゃないの?!」
僕「そこだよ! 海の波が伝わるとき、海の水が動くわけじゃないんだ。 ああ、もちろん、波打ち際で小さな水の移動はあるし、 波が伝わるときには水はその場で小さく回転運動をしてる。 でもね、海の波が遠くまで伝わるというのは、 海の水が遠くまではるばる移動するわけじゃない。 水が移動してるんじゃなく、ただ、振動が伝わるだけなんだ。 ある地点の振動のパターンが、少しずつ遠くまで伝わっていく。 それが波」
ユーリ「そっか!」
僕「音もそうだよ。音は遠くまで伝わる。 あれは、あくまで空気の振動が伝わっているだけであって、 空気が遠くまで風のように移動しているわけじゃないんだ」
ユーリ「そーなんだ!」
僕「地震の波を考えれば、もっとよくわかる。 土や岩がゴゴゴゴっと移動してくるわけじゃなくて、 振動が伝わってくるんだよね?」
ユーリ「う、うわああ……」
僕「物理で扱う波について、もう少し考えを進めてみるよ。 波というと、こんな図形を思い描くよね」

ユーリ「うん、そだね。まさに波」
僕「さっき僕たちは《振動が伝わっていく現象》のことを波と呼んだけれど、 波は、この図形とどんな関係があるのか、それを考えてみよう。 つまり、この図形は《振動が伝わっていく現象》をどんなふうに表しているんだろうか」
ユーリ「?」
僕「こう言い換えようか。 この図形を《波を表すグラフ》としたとき、横軸と縦軸は何だろう?」

ユーリ「横軸は $x$ 軸で、縦軸は $y$ 軸じゃないの?」

僕「ユーリが $x$ と $y$ と名前を付けたものは、 いったい何を表しているか、というのが問題。 たとえば、海の波が伝わるとき」
ユーリ「ええと? ……うん、わかった! 《振動が伝わっていく現象》を表すんでしょ? だから、 $x$ は《位置》を表してる! ここでの波があっちの方に伝わっていくんだから、 $x$ は海の上の《位置》だよね。そして、 $y$ は水の高さ……《水位》だ! だって、上がったり下がったりする振動が遠くまで伝わるんだから」
僕「いいね! じゃ、ユーリのいう通り考えてみるよ。 そうすると、このグラフを見たとき、 位置 $x$ が $0$ での水位 $y$ は $0$ になるわけだね。 そして、位置 $x$ が $a$ での水位 $y$ は $b$ になると」
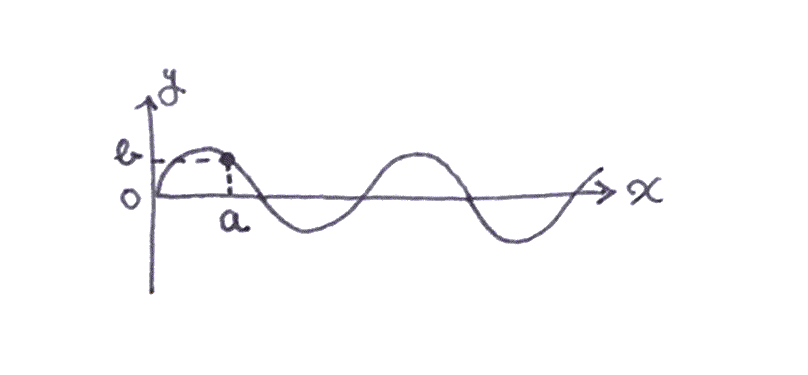
ユーリ「そーそー!」
僕「ということは、 このグラフはある時刻で海面をパチリと写真に撮ったようなものだね?」
ユーリ「え……」
僕「なぜかというと、この位置での水位、あの位置での水位……は、 このグラフでよくわかるけれど、一秒後にどうなるか、 一秒前にどうなっていたかは、何も表していない。 時刻に関わる要素は、このグラフでは何も表されていないから」
ユーリ「う……」
僕「そうなんだよ、ユーリ。ユーリが $x$ 軸と $y$ 軸を定めてくれたこのグラフは、 確かに波のグラフといえる。 でもある時刻でのスナップショットにすぎない。 このグラフ、つまり《位置と水位のグラフ》だけでは、 波が《伝わっていく》ようすは何も表されていないことになる」
《位置と水位のグラフ》

ユーリ「確かに……」
僕「ユーリがグラフを描くとき、お兄ちゃんはいつも《軸は何か?》 と聞く理由がわかっただろ? 軸を確認することはとても大事。 波動では特に大事」
ユーリ「ねー、でも、このグラフもまちがいじゃないよね?」
僕「うん、まちがいじゃない。ぜんぜんまちがいじゃない。 波を、ある時刻でパチリと写真を撮ったようなものだというだけ」
ユーリ「時刻……じゃ、時刻を横軸にするの?」
僕「横軸が時刻 $t$ になっているグラフを描いてみると、 たとえば、こんなふうになるね」
《時刻と水位のグラフ》
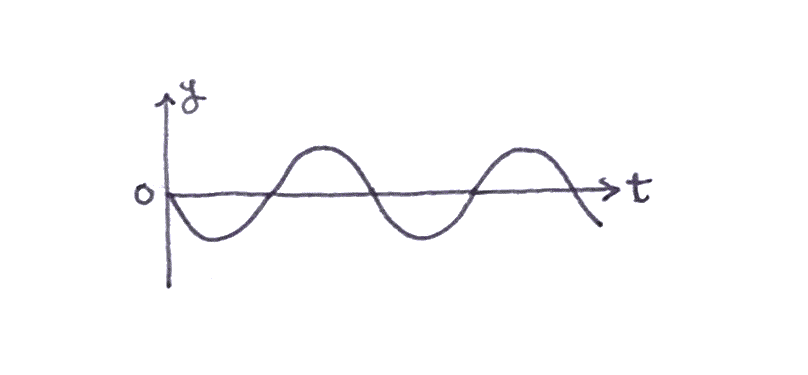
ユーリ「……」
僕「じゃ、このグラフは、いったい何を表しているんだろう?」
ユーリ「いまそれ考えてるの!」
僕「じっくり考えていいよ」
僕はユーリが集中思考モードになっているのを眺める。
ユーリは基本的にめんどうくさがりで飽きっぽいけれど、 決していいかげんじゃない。退屈なのが嫌いなだけなんだ。
ユーリ「……ねえ、お兄ちゃん」
僕「なに?」
ユーリ「このグラフの横軸は時刻なんだよね?」
《時刻と水位のグラフ》

僕「そうだね。《時刻と水位のグラフ》では、時刻 $t$ が横軸」
ユーリ「だったら、このグラフは時刻ごとの水位を表しているんだよね?」
僕「うんうん、そうなるね」
ユーリ「たとえば、時刻 $t$ が $0$ のときの水位、時刻 $t$ が $1$ のときの水位を表していて……もちろん、途中の $t = 0.5$ とかも表してる」
僕「いいねえ、その通り。このグラフでは具体的な目盛りを振ってないけど、ユーリがいうのは正しいよ」
ユーリ「だから、時刻が過ぎていくときに水位がどう変わるのかわかる……っていうグラフ?」
僕「うん、それでいいよ」
ユーリ「えー、でもね、それじゃ、一か所しか見てないじゃん!」
僕「その通り! そうなんだよ。 このグラフ、《時刻と水位のグラフ》は、どこかに位置を定めておいて、 時刻ごとの水位を表していることになるね」

ユーリ「じゃあさ、このグラフ……この、横軸が $t$ 軸で、縦軸が $y$ 軸のグラフだと、 《波が伝わっていく》のは、やっぱり表せてない。 だって、このグラフだと、どこかの位置の水位をじーっと見てるだけなんでしょ? それじゃ、ほら、 さっきお兄ちゃんが指を振ってたのと同じことじゃん!」
僕「ユーリは正しいよ。その理解で正しい。 さっきの《位置と水位のグラフ》の方では時刻が固定されていた。 そしていまの《時刻と水位のグラフ》では位置が固定されている」
僕「このどちらのグラフも、 一枚だけでは《振動が伝わっていく現象》の《伝わっていく》ところ、 肝心のところは表せていないことになるね」
ユーリ「だめじゃん!」
僕「グラフ一枚だけならね。だったら、複数枚を使えばいい」
ユーリ「複数枚?」
僕「そうだよ。たとえば《位置と水位のグラフ》をこんなふうに四枚用意してみよう。 この四枚は、時刻を変えて波の写真を撮ったものとする」
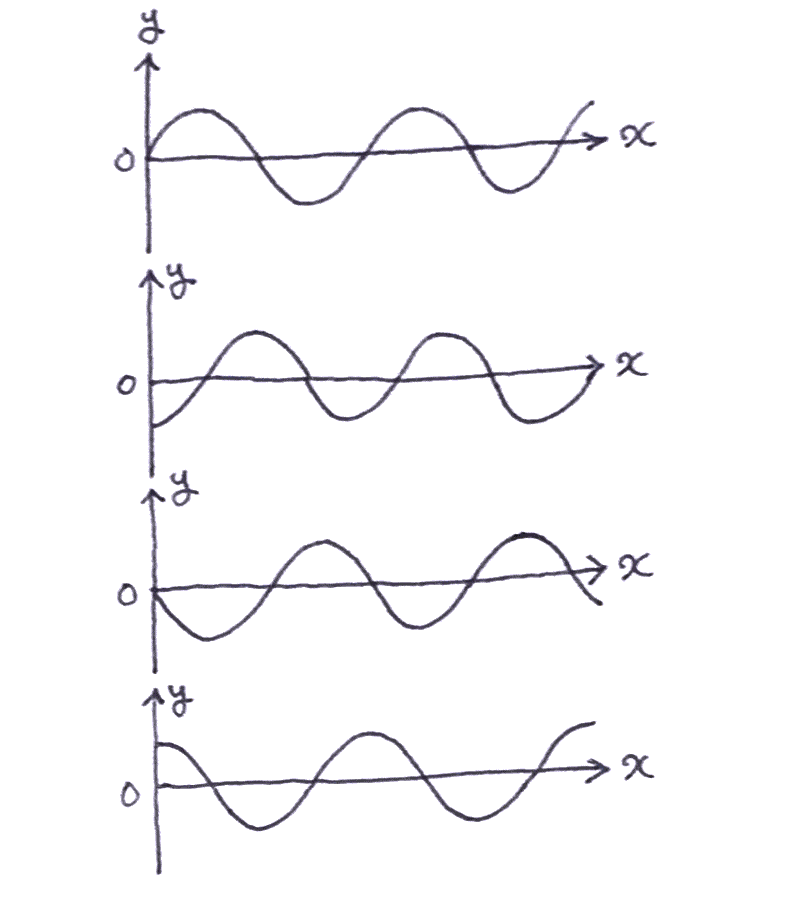
ユーリ「ははーん。なるほどね! うねうね動いてくんだ!」
僕「この四枚のグラフにこんなふうに印を付けてみよう。 波の《山》の部分に印を付けたよ。 ほら《伝わっていく》ようすが見えてくるよね!」
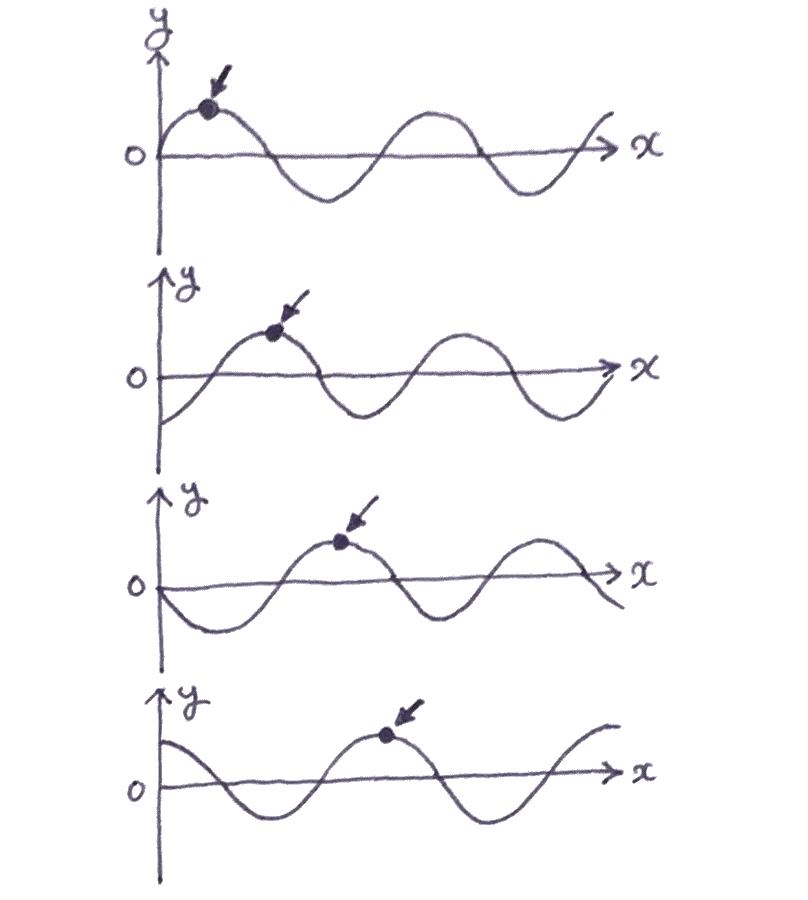
ユーリ「うん、見える見える! 山が動いてる」
僕「《山》になった状態がその位置を変えていくのであって、 水が動いているわけじゃないんだけどね」
ユーリ「わかってるよ」
僕「さて、ここからがおもしろいところだよ、ユーリ」
ユーリ「なに腕まくってんの」
僕「さっき、《ボールが飛んでいく》のと《波が伝わる》のとは違うっていったよね。 ボールが飛んでいくときにはボールという物質が移動していく。 でも、波が伝わるときには物質が移動していくわけじゃなくて、 振動のパターンが移動していくわけだね。《山》の部分が移動していくように」
ユーリ「そーだけど?」
僕「ある時刻では《山》はこの位置にあり、別の時刻では《山》は別の位置にある。 つまり、波の《山》は移動していくわけだ。移動するのは《山》だけじゃなく《谷》の部分もだけど」
ユーリ「そりゃそーだ」
僕「《時刻の変化》に合わせて《位置の変化》があるんだから、 つまり、波について《速度》を考えることができるよね! ボールや歩く人や自動車の速度を考えるのと同じようにね!(『数学ガールの秘密ノート/微分を追いかけて』参照)」
ユーリ「おー! 確かに!」
僕「波は《振動が伝わっていく現象》だ。 言い換えると、時刻が経過するごとに振動のパターンが位置をどんどん変えていく、 といえる。だから、その《位置の変化》を《時刻の変化》で割ってやれば、 波が伝わる速度を求めることができる、ということになるよね? 《時刻の変化》というのは経過した時間のことだよ」
《速度》=《位置の変化》÷《時刻の変化》
ユーリ「速度……波にも速度があるんだ。 あっ、そーいえば、習ったよ。音の速さって、秒速 $340$ メートルじゃなかった?」
僕「それそれ。速さというのは速度の大きさだね。 温度で速さは変わるけれど、だいたい秒速 $340$ メートルになる。 言い換えると、 $1$ 秒経過すると、音の波は $340$ メートル進むということになる」
ユーリ「ふんふん」
僕「波の速度の話が、これまたおもしろいんだよ!」
ユーリ「お兄ちゃん、楽しそーだね」
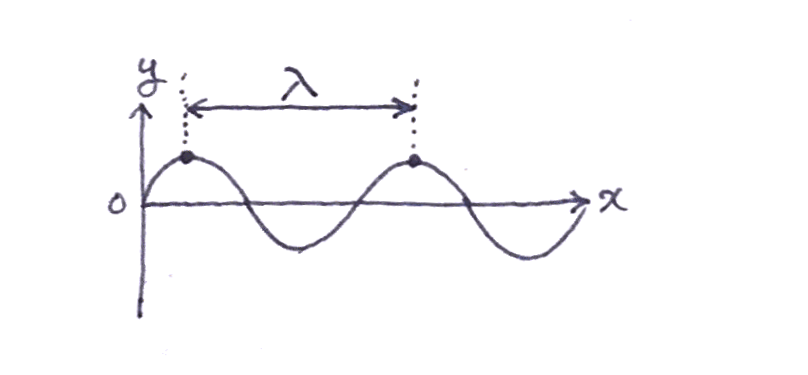
僕「ここに、海の波を表したグラフを二つ描いてみた。 片方は、時刻が $0$ での《位置と水位のグラフ》で、 もう片方は、位置が $0$ での《時刻と水位のグラフ》としようか」
$t = 0$ での《位置と水位のグラフ》
$x = 0$ での《時刻と水位のグラフ》
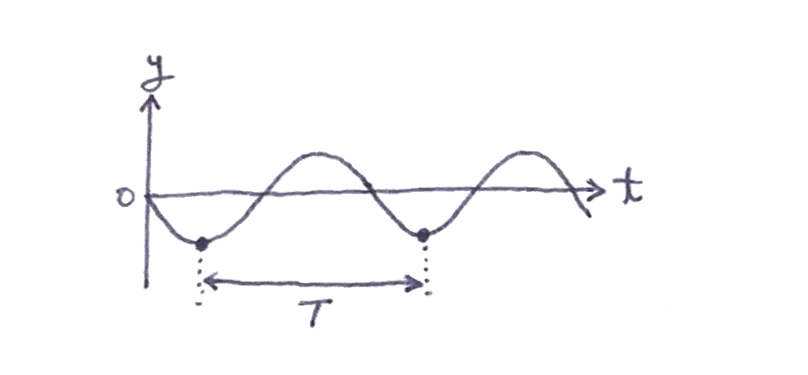
ユーリ「うん。この《入る》ってゆーのは何?」

僕「これは、《入る》じゃなくて、ラムダって読むんだよ」
ユーリ「らむだ」
僕「$\lambda$(ラムダ)はギリシア文字。 英語のアルファベットでいえば、l(エル)に相当する文字かな。 波では、波長(はちょう)のことを $\lambda$ で表すことが多いんだ」
ユーリ「はちょう」
僕「波長っていうのは《波一つ分の長さ》のことだね。山から山までの距離でもいいし、谷から谷までの距離でも同じだけど」
ユーリ「ふーん」
僕「そして、こっちの $T$(ティー)は、周期(しゅうき)という。 周期っていうのは《振動一回分に掛かる時間》のこと」

ユーリ「振動一回分……」
僕「なぜかというと」
ユーリ「待って! いま考えてんだから……」
僕「はいはい。ごめんごめん」
ユーリ「……」
僕「……」
ユーリ「そっか、わかった! 《振動一回分》の意味、わかったよ」
僕「お、そりゃすごいな」
ユーリ「簡単な話じゃん。 グラフの通り! だって、この《時刻と水位のグラフ》は、 位置を固定してるんでしょ? つまり、一つの場所をじっと見てる。 じっと見てると、時間が経つごとに水位が《谷》から上がって、下がって、 もとの《谷》まで戻る。だから《振動一回分》なんでしょ?」

僕「そうそう! その通り。そして、 $T$ はその《振動一回分》に掛かる時間を表しているんだよ。それが周期 $T$」
ユーリ「ふんふん。《谷》になってから、次に《谷》になるまでだから……納得納得。波長 $\lambda$ も周期 $T$ もカンタンじゃん」
僕「ほんとうにわかったかなあ……じゃあ、ここでユーリに問題を出すよ」
ユーリ「どんとこい」
僕「この波の速度を $v$(ヴィ)としたとき、 《速度 $v$》を《波長 $\lambda$》と《周期 $T$》で表せ。これが問題」
問題(波の速度・波長・周期)
以下のグラフは、ある波を表している。 この波の速度を $v$ としたとき、 $v$ を $\lambda$ と $T$ で表せ。


ユーリ「むむむ? 波の速度?」
僕「続きは後編にて!」
ユーリ「メタ発言禁止!」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 420本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第141回終わり)
(2016年1月8日)
この記事は『数学ガールの物理ノート/波の重ね合わせ』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!