![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの物理ノート/波の重ね合わせ』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。好奇心旺盛で根気強い《元気少女》。
ミルカさん:数学が好きな高校生。僕のクラスメート。長い黒髪の《饒舌才媛》。
瑞谷先生:司書の先生。定時になると下校時間を宣言する。
僕「ともかく、答えをまとめてみるよ」
解答1(?)
数列 $a_n,b_n$ を、 $$ \left\{\begin{array}{llll} a_n &= \dfrac{1}{\pi} \int_{0}^{2\pi} f(x)\cos nx \,dx \\ b_n &= \dfrac{1}{\pi} \int_{0}^{2\pi} f(x)\sin nx \,dx \\ \end{array}\right. $$ のように定めると、 $$ f(x) = \sum_{k = 0}^{\infty} (a_k\cos kx + b_k\sin kx) $$ が成り立つ。
テトラ「……」
ミルカ「……」
僕「そうだ。具体例に進もうよ! 僕が具体例を持ってる。 先日、ユーリと遊んだときにちらちらと見えていた《波》だ。 この平らな波をフーリエ展開してみよう!」
ミルカ「ふむ、それもいいが、その前にやることがある」
僕「やること?」
ミルカ「この《解答1(?)》の誤りを一つ見つけること。フーリエ展開の可能性という話ではなく、単純な誤りを」
僕「単純な誤りがあるって?」
テトラ「……」
僕「収束条件ではないんだよね?」
ミルカ「フーリエ展開ができる $f(x)$ の条件ではないし、 関数の収束条件でもない。もっと単純で、明白な誤りがある」
テトラ「あ、あのですね……《$n$ の条件》でしょうか?」
ミルカ「テトラはそれを具体的に言う」
テトラ「あたしが計算していた定積分では、 $m$ も $n$ も《$1$ 以上の整数》という条件が付いていました。 でも、先ほどの先輩の解答1(?)では、 $a_n$ や $b_n$ に対する $n$ に何も条件が付いていなかったので……」
僕「ちがうよ、テトラちゃん」
ミルカ「そこだよ、テトラ」
僕「あれ? 確かにさっきの解答では条件を付けなかったけど、 $n$ は $0$ 以上の整数にして構わないはずだよ」
ミルカ「$n = 0$ でも?」
僕「大丈夫。だって、 $\cos nx = \cos 0x = 1$ だし、 $\sin nx = \sin 0x = 0$ になるだけのことだから。 つまり、 $n = 0$ のときは自動的に、 $$ \left\{\begin{array}{llll} a_0 &= \dfrac{1}{\pi} \int_{0}^{2\pi} f(x)\cos 0x \,dx \\ &= \dfrac{1}{\pi} \int_{0}^{2\pi} f(x) \,dx \\ b_0 &= \dfrac{1}{\pi} \int_{0}^{2\pi} f(x)\sin 0x \,dx \\ &= 0 \\ \end{array}\right. $$ になってくれる。つまり $f(x)$ の定数項として、 $a_0$ を作り出すことができるはず。 これは、 $\sum$ と $\int$ の交換や関数の収束を前提とすれば、 証明もできるはずだよ」
ミルカ「どんなふうに?」
僕「こんなふうに……ええと、要するに、 $$ f(x) = \sum_{k=0}^{\infty} \left(a_k\cos kx + b_k\sin kx\right) $$ に対して $$ \dfrac{1}{\pi} \int_{0}^{2\pi} f(x) \,dx $$ という定積分を実行すればいいんだよ。それでちゃんと $a_0$ が出てくるから」
テトラ「それは先ほどやったような……(第149回参照)」
僕「うん、さっきは一般的にさらっと書いたから、 $n = 0$ のときを明示的にやってみればいいだけのこと。この定積分だね」
$$ \begin{align*} \dfrac{1}{\pi}\int_{0}^{2\pi} \left\{\sum_{k=0}^{\infty} \left(a_k\cos kx + b_k\sin kx\right) \right\} \, dx &= \cdots \\ \end{align*} $$僕「これで $k = 0$ の項だけを外に出して、 $\cos 0x = 1$ と $\sin 0x = 0$ を使う」
$$ \begin{align*} & \dfrac{1}{\pi}\int_{0}^{2\pi} \left\{\sum_{k=0}^{\infty} \left(a_k\cos kx + b_k\sin kx\right) \right\} \, dx \\ &= \dfrac{1}{\pi}\int_{0}^{2\pi} \left\{a_0\cos 0x + b_0\sin0x + \sum_{k=1}^{\infty} \left(a_k\cos kx + b_k\sin kx\right) \right\} \, dx \\ &= \dfrac{1}{\pi}\int_{0}^{2\pi} \left\{a_0 + \sum_{k=1}^{\infty} \left(a_k\cos kx + b_k\sin kx\right) \right\} \, dx \\ \end{align*} $$テトラ「……」
僕「次に、積分と和の交換。ここはほんとうはちゃんと証明が要るはずだけど」
$$ \begin{align*} \cdots &= \dfrac{1}{\pi}\int_{0}^{2\pi} a_0 \, dx + \dfrac{1}{\pi}\sum_{k=1}^{\infty} \left(\int_{0}^{2\pi} a_k\cos kx + b_k\sin kx \, dx \right) \\ \end{align*} $$ミルカ「……」
僕「この $\sum$ の中は $k$ 回振動する $\cos$ や $\sin$ だから、 $0$ から $2\pi$ まで積分したら結局 $0$ になる。残りは定数の積分だから……」
$$ \begin{align*} \cdots &= \dfrac{1}{\pi}\int_{0}^{2\pi} a_0 \, dx + 0 && \REMTEXT{($\sum$ の中はすべて$0$)} \\ &= \dfrac{1}{\pi}\biggl[\,\, a_0x \,\,\biggr]_{0}^{2\pi} \\ &= \dfrac{1}{\pi}\left( a_0\cdot 2\pi - a_0\cdot 0\right) \\ &= \dfrac{1}{\pi}\cdot 2\pi a_0 \\ &= 2a_0 \quad \REMTEXT{えっ!?} \\ \end{align*} $$僕「えっ!?」
テトラ「定積分の結果、 $a_0$ が出てくるはず……ですが?」
僕「$2a_0$ になってしまった……」
ミルカ「だから、そこが誤り。いま君が計算してくれたとおり、 $n = 0$ のとき、同じ式ではフーリエ係数は得られない。 同じ式では $2$ 倍になってしまう。だから、フーリエ係数を求める式はこれが正しい。 $a_0$ の分母に注意」
解答1
数列 $a_n,b_n$ を、 $$ \left\{\begin{array}{llll} a_0 &= \dfrac{1}{2\pi} \int_{0}^{2\pi} f(x) \,dx \\ b_0 &= 0 \\ a_n &= \dfrac{1}{\pi} \int_{0}^{2\pi} f(x)\cos nx \,dx \qquad (n = 1,2,3,\ldots)\\ b_n &= \dfrac{1}{\pi} \int_{0}^{2\pi} f(x)\sin nx \,dx \\ \end{array}\right. $$ のように定めると、 $$ f(x) = \sum_{k = 0}^{\infty} (a_k\cos kx + b_k\sin kx) $$ が成り立つ。
僕「うわ、 $a_0$ だけ違うのか! これは、意外な落とし穴だなあ……」
テトラ「条件を確認するのは大事なんですね……」
ミルカ「$a_0 = \dfrac{1}{\pi} \int_{0}^{2\pi} f(x) \,dx$ のままで行くなら、 $$ f(x) = \frac{a_0}{2} + \sum_{k = 1}^{\infty} (a_k\cos kx + b_k\sin kx) $$ のように表す方法もある」
僕「なるほど」
ミルカ「話が飛んでしまった。君がフーリエ展開したいといってた波があったね」
僕「そうそう。これはね、このあいだユーリと遊んでいたときに気になってた波なんだ。 $$ \frac{\sin1x}{1} + \frac{\sin3x}{3} + \frac{\sin5x}{5} + \cdots $$ のように奇数 $n$ を使って $\frac{\sin nx}{n}$ の和を作ると、 こんなふうに四角い波っぽくなったんだよ」
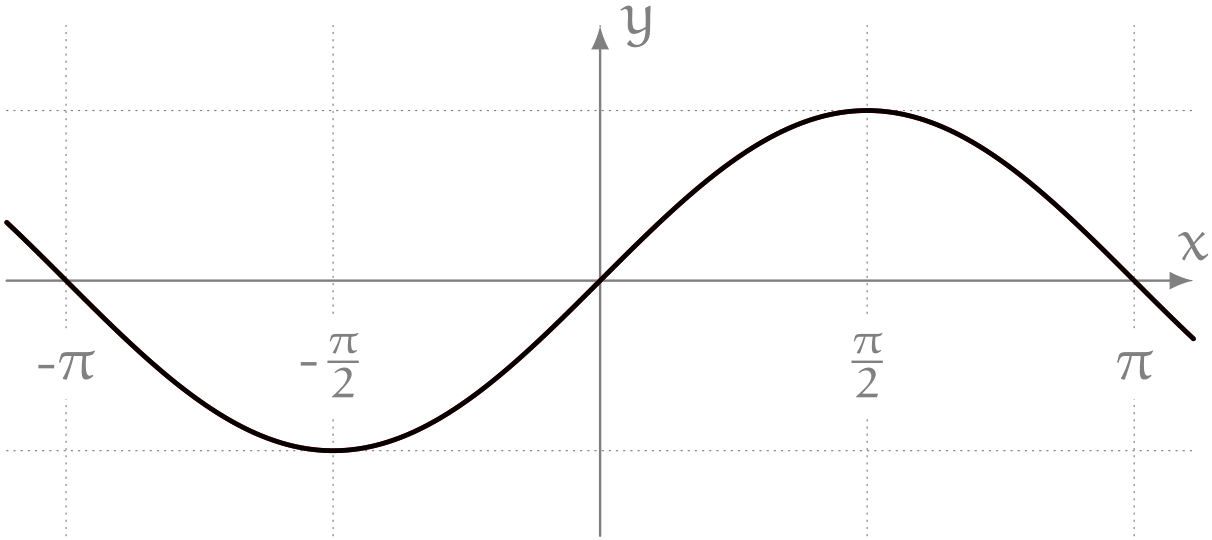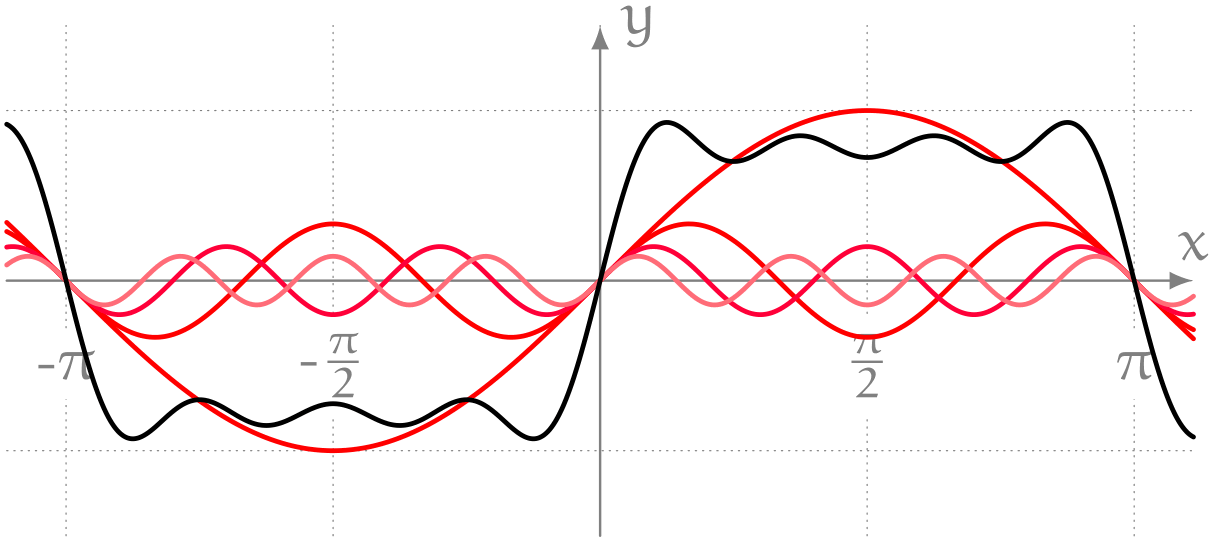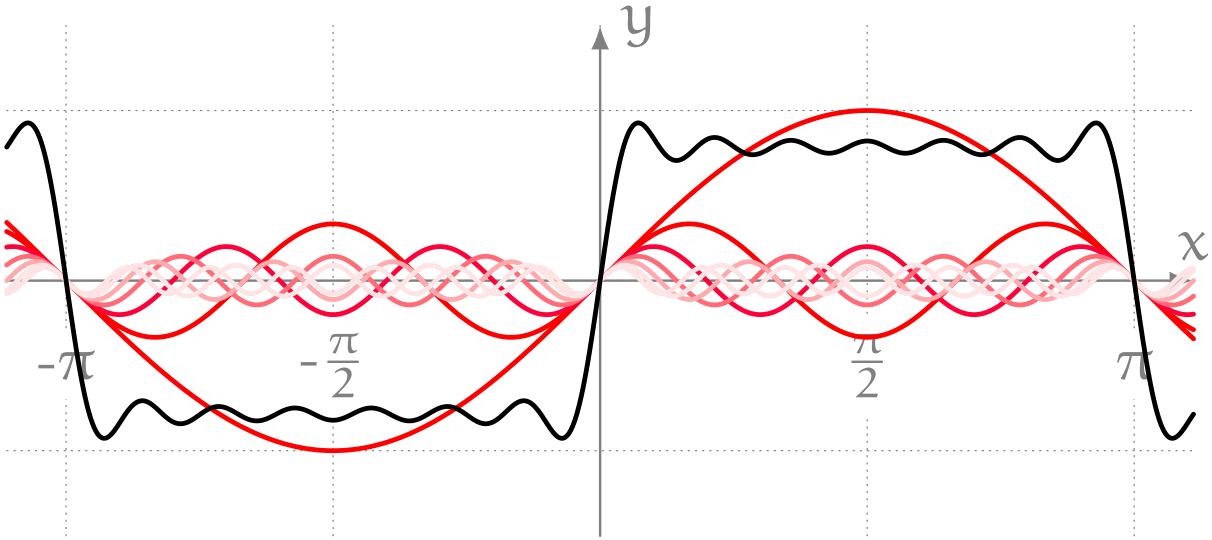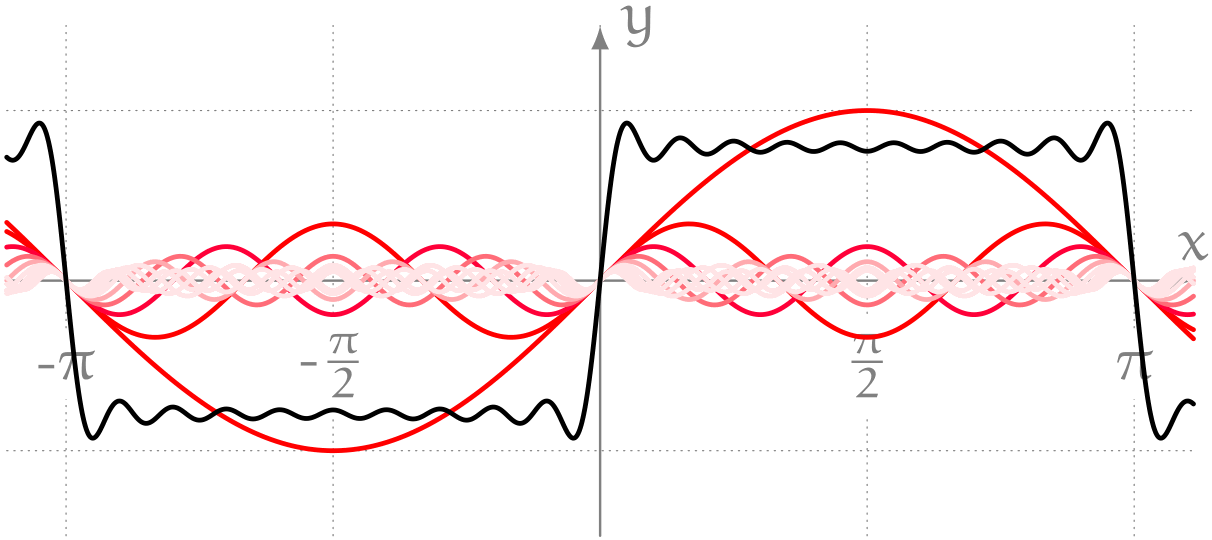
ミルカ「ふむ」
僕「だから、こういう平らな波を考えてみたいんだ」

ミルカ「矩形波(くけいは)だね」
僕「矩形波? うん、だから、その矩形波のグラフを $y = f(x)$ だと考えれば、 フーリエ展開の方法で $\dfrac{\sin nx}{n}$ という形の項が出てくるんじゃないかって……そう思わない?」
ミルカ「それは確かに出てきそうだな」
僕「だよね」
テトラ「せ、先輩方! ただいま、テトラは置いてけぼりになりかけています! しばし、お待ちを! 頭を整理させてください」
僕「係数を掛けた上で加えるんだね」
ミルカ「線型結合」
テトラ「あ、そうでした。そうでした」
僕「数列 $a_n$ と $b_n$ を求める方法だね」
ミルカ「フーリエ係数」
テトラ「ですね!」
僕「そしてこれから、矩形波を実際に定積分して、ほんとうにフーリエ係数が求まるかを試してみようとしているわけだね」
テトラ「ふう……ようやく先輩方に追いつきましたっ!」
ミルカ「問題を立てると、こうなるな」
問題2
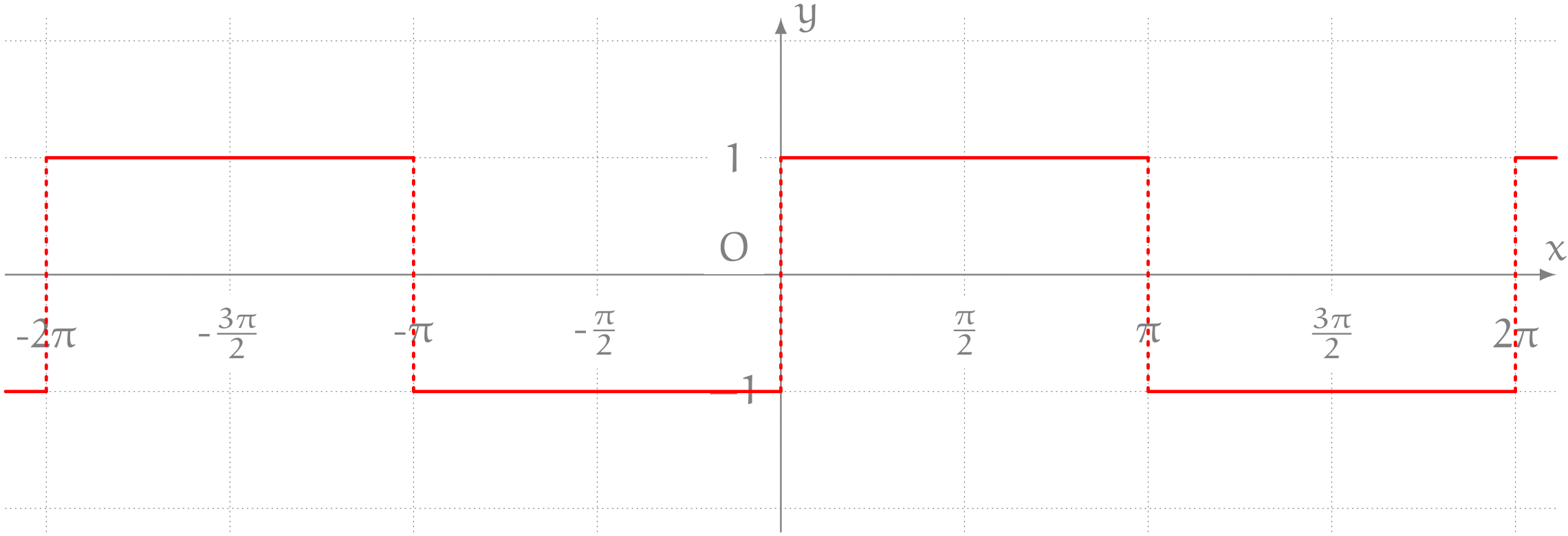
グラフが以下のようになる関数 $y = f(x)$ がある。

$f(x)$ が、 $$ f(x) = \sum_{k=0}^{\infty}\left(a_k\cos kx + b_k\sin kx\right) $$
とフーリエ展開できると仮定して、 フーリエ係数 $a_0,a_1,a_2,\ldots,b_0,b_1,b_2,\ldots$ を求めよ。

テトラ「……先輩、でも、こんなにがたがたになった関数の積分なんてできるんですか? あたしができる積分というのは、 $x^2$ や $e^x$ や $\sin x$ や $\cos x$ や……ぜんぶ、つながった関数なんですけれど」
僕「うん、そうだね。僕たちがふだん問題で解くのはつながった関数……連続関数のことが多いけど、 これは大丈夫。積分区間で分けて考えればいいんだよ。 ほら、たとえば、 $x$ が $0$ から $\pi$ までの範囲では、 $f(x)$ は $1$ という《定数関数》になるよね?」
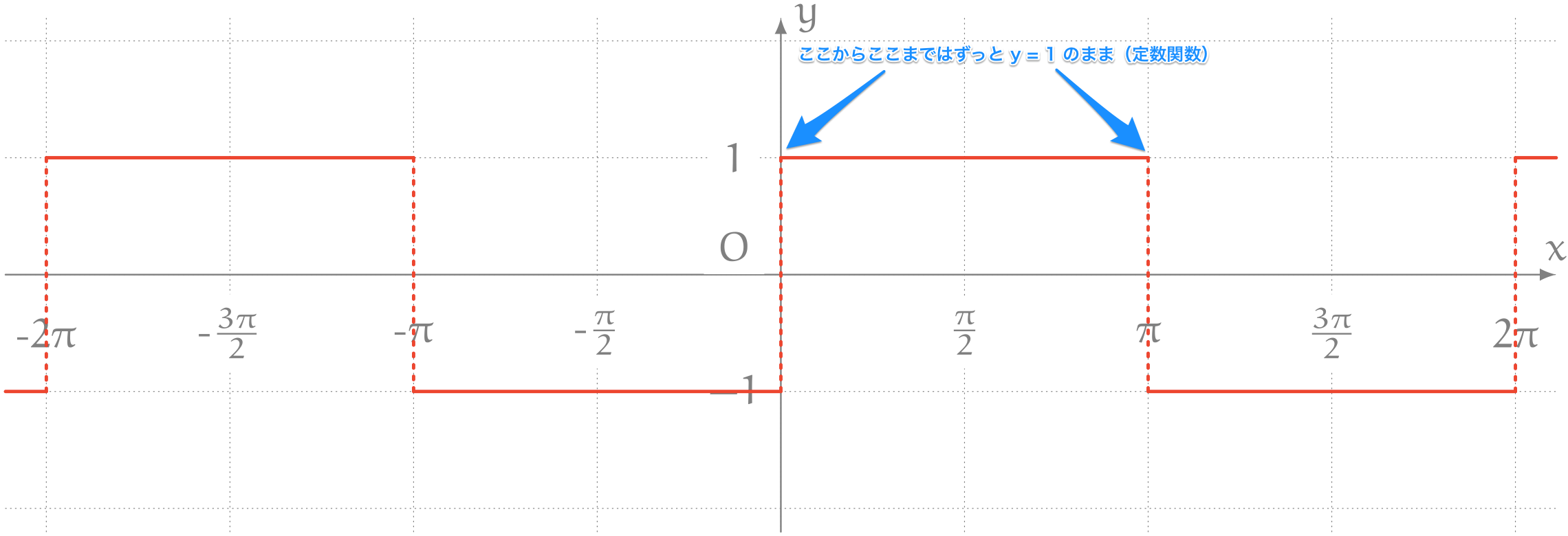
テトラ「……あっ、そうですね。定数関数の積分はあたしもできます! ははあ……ここにも《場合分け》が出てくるんですね」
僕「積分は結局は和なんだから、積分区間で足せばいいし」
ミルカ「まず、 $f(x)$ を……」
僕「そうだね。まず $f(x)$ を式で表さないと。やみくもに積分積分と言ってもばかりいてもしょうがないから。 グラフから、たとえばこんなふうに書けるね。 $$ f(x) = \left\{\begin{array}{llll} 1 & && 2n\pi \leqq x < (2n+1)\pi \\ -1 & && (2n+1)\pi \leqq x < 2(n+1)\pi \\ \end{array}\right. $$ ただし、 $n$ は整数」
テトラ「ちょっとお待ちください。 $n = 0$ のときは $0 \leqq x < \pi$ で $f(x) = 1$ で、 $\pi \leqq x < 2\pi$ で $f(x) = -1$ ですね……はい、わかりました。 これは《$\pi$ の偶数倍》と《$\pi$ の奇数倍》の範囲をつなぎあわせているんですね」
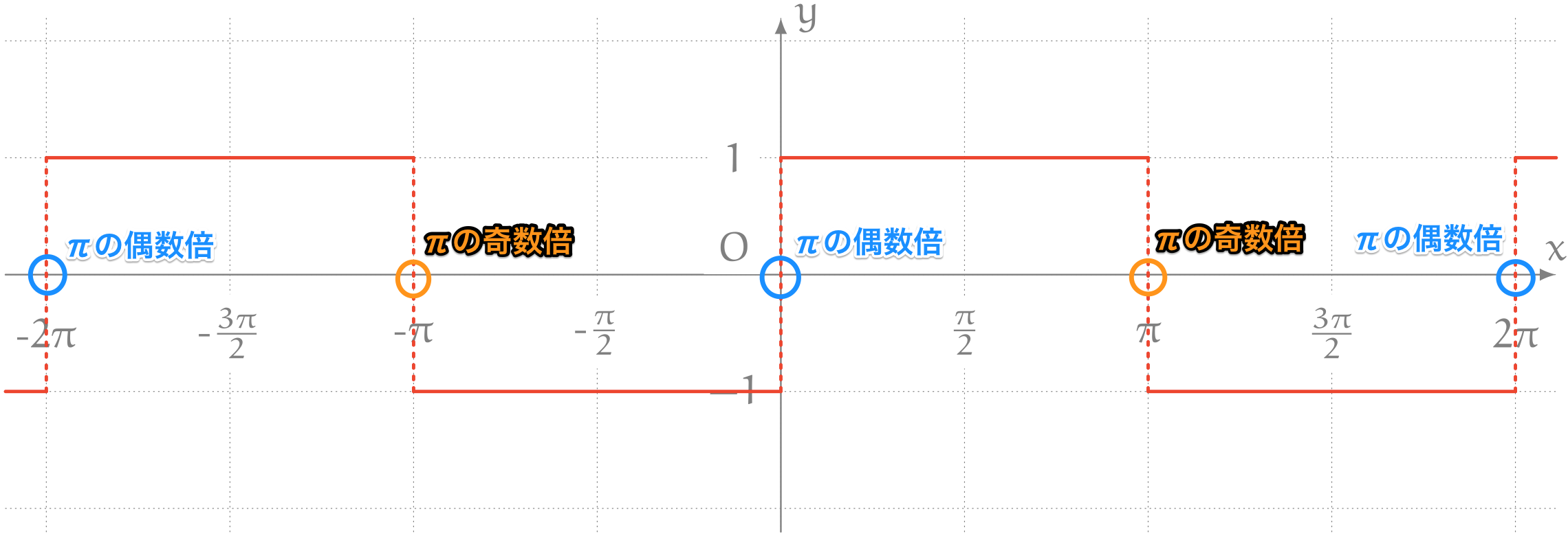
僕「$a_0$ から行くよ。これは一瞬だね」
$$ \begin{align*} a_0 &= \dfrac{1}{2\pi} \int_0^{2\pi} f(x) \, dx \\ &= \dfrac{1}{2\pi} \left(\int_0^{\pi} f(x) \,dx + \int_{\pi}^{2\pi} f(x) \,dx \right) \qquad \REMTEXT{積分区間を分けた}\\ &= \dfrac{1}{2\pi} \left(\int_0^{\pi} 1 \,dx + \int_{\pi}^{2\pi} (-1) \,dx \right) \qquad \REMTEXT{場合分けした$f(x)$より} \\ &= \dfrac{1}{2\pi} \left(\biggl[\,\, x \,\,\biggr]_0^{\pi} + \biggl[\,\, -x \,\, \biggr]_{\pi}^{2\pi}\right) \qquad \REMTEXT{積分した} \\ &= \dfrac{1}{2\pi} \left(\pi - 0 + (-2\pi) - (-\pi) \right) \\ &= 0 \\ \end{align*} $$ミルカ「ふむ。 $f(x)$ は奇関数だから、 $0$ になるのは予想が付くな」
僕「なるほどね。偶関数である $\cos nx$ の係数は $0$ になるわけだね」
ミルカ「もちろん、いまは計算練習をしているわけだから、それは検算用の考えになるけれど」
テトラ「あ、あの、 $b_0$ も一瞬です!」
ミルカ「$0$ だからな」
僕「$0$ だからね」
テトラ「……です」
僕「じゃ、今度は $n = 1,2,3,\ldots$ のときの $a_n$ を求めるよ。 基本はさっきと同じように積分区間を分けるんだけど、今度は $\cos nx$ が出てくるわけだよね」
$$ \begin{align*} a_n &= \dfrac{1}{\pi} \int_{0}^{2\pi} f(x)\cos nx \,dx \\ &= \dfrac{1}{2\pi} \left(\int_0^{\pi} f(x)\cos nx \,dx + \int_{\pi}^{2\pi} f(x)\cos nx \,dx \right) \\ &= \dfrac{1}{2\pi} \left(\int_0^{\pi} \cos nx \,dx + \int_{\pi}^{2\pi} (-\cos nx) \,dx \right) \\ &= \dfrac{1}{2\pi} \left(\biggl[\,\, \frac{\sin nx}{n} \,\,\biggr]_0^{\pi} + \biggl[\,\, -\frac{\sin nx}{n} \,\, \biggr]_{\pi}^{2\pi}\right) \\ &= \dfrac{1}{2\pi} \left(0 - 0 + (-0) - (-0) \right) \\ &= 0 \\ \end{align*} $$僕「うん、やはり予想通り $0$ になったね」
テトラ「……先輩、この途中の式なんですが」
$$ \cdots = \dfrac{1}{2\pi} \left(\int_0^{\pi} \cos nx \,dx + \int_{\pi}^{2\pi} (-\cos nx) \,dx \right) $$テトラ「これって、このようにマイナスを前に出すことができますよね?」
$$ \cdots = \dfrac{1}{2\pi} \left(\int_0^{\pi} \cos nx \,dx - \int_{\pi}^{2\pi} \cos nx \,dx \right) $$僕「うん、そうだね」
テトラ「だったら、同じ $\cos nx$ という関数を積分しているんですから、 $\int_{0}^{\pi}$ と $\int_{\pi}^{2\pi}$ という二つの積分区間を一つにまとめて $\int_{0}^{2\pi}$ にしてもいいですよね。 つながっている区間で同じ関数を積分するんですから。 それなら、一気に $0$ だと求められますよ!」
$$ \begin{align*} \cdots &= \dfrac{1}{2\pi} \left(\int_0^{\pi} \cos nx \,dx - \int_{\pi}^{2\pi} \cos nx \,dx \right) \\ &= \dfrac{1}{2\pi} \left(\int_0^{2\pi} (\cos nx - \cos nx) \,dx \right) \quad \REMTEXT{(?)} \\ &= 0 \\ \end{align*} $$僕「ああなるほど……じゃない、それはだめだよ、テトラちゃん。 そんなことをしたら、二つの関数を別の区間まで伸ばして積分してることになるから」
テトラ「え……?」
ミルカ「それでは伝わらない。テトラの混乱は、一般的に書けばすぐ解ける。 いまテトラがやろうとした積分の操作はこれだ。こんなことはできない」
$$ \int_0^\pi f(x) \,dx - \int_\pi^{2\pi} g(x) \,dx = \int_0^{2\pi} \left(f(x) - g(x) \right) \,dx \qquad \REMTEXT{(?)} $$テトラ「あっ、そうですね。うっかりしました。 $\cos nx$ という同じ顔を見てしまったもので……」
ミルカ「ここまでで $a_0 = a_1 = a_2 = \cdots = 0$ が得られた。偶関数の成分はすべて $0$ だ」
僕「いよいよ $b_n$ だね」
テトラ「あ、あたし、計算します! 式の途中までは先ほどと同じですから……」
$$ \begin{align*} b_n &= \dfrac{1}{\pi} \int_{0}^{2\pi} f(x)\sin nx \,dx \\ &= \dfrac{1}{2\pi} \left(\int_0^{\pi} f(x)\sin nx \,dx + \int_{\pi}^{2\pi} f(x)\sin nx \,dx \right) \\ &= \dfrac{1}{2\pi} \left(\int_0^{\pi} \sin nx \,dx + \int_{\pi}^{2\pi} (-\sin nx) \,dx \right) \\ &= \dfrac{1}{2\pi} \left(\biggl[\,\, \frac{-\cos nx}{n} \,\,\biggr]_0^{\pi} + \biggl[\,\, -\frac{-\cos nx}{n} \,\, \biggr]_{\pi}^{2\pi}\right) \\ &= \dfrac{1}{2\pi} \left(\frac{-\cos n\pi}{n} - \frac{-\cos 0n}{n} - \frac{-\cos 2n\pi}{n} + \frac{-\cos n\pi}{n} \right) \\ &= \dfrac{1}{2\pi} \left(- \frac{\cos n\pi}{n} + \frac{1}{n} + \frac{1}{n} - \frac{\cos n\pi}{n} \right) \\ &= \dfrac{1}{2n\pi} \left(2 - 2\cos n\pi \right) \\ &= \dfrac{1}{n\pi} \left(1 - \cos n\pi \right) \\ &= \dfrac{1 - \cos n\pi}{n\pi} \\ &= \REMTEXT{あ、あれれ……?} \\ \end{align*} $$テトラ「あ、あれれ……? あたし、計算ミスしてます?」
僕「どうして、そう思ったの?」
テトラ「だって、 $\cos$ が出てしまいました。先輩、先ほど $\frac{\sin nx}{n}$ になるとおっしゃってませんでしたか? $\sin$ が出るはずなのに、 $\cos$ が出てきました!」
僕「テトラちゃん、テトラちゃん、落ち着いて。さっき僕がいった $\frac{\sin nx}{n}$ というのは、 和の各項だから、係数には $\sin$ は出てこないよ。 $\sin nx$ の係数は $\frac{1}{n}$ だね」
テトラ「だったら、なおさらです。 $\cos$ が出てきたら……」
ミルカ「テトラは $\cos n\pi$ が三角関数に見えるのか」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 420本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2016年3月11日)
この記事は『数学ガールの物理ノート/波の重ね合わせ』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!