![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/複素数の広がり』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。好奇心旺盛で根気強い《元気少女》。
僕とテトラちゃんは、正 $5$ 角形をめぐる数学トークを続けている。
テトラ「あ、これ、 $2$ 次方程式になってます! ここ、同じですから!」
$$ \underline{(z + \BAR{z})}^2 + \underline{(z + \BAR{z})} - 1 = 0 $$僕「そうだね。できた、できた! これで解けるよ。 $y = z + \BAR{z}$ と置いてみよう」
$$ \begin{align*} (z + \BAR{z})^2 + (z + \BAR{z}) - 1 &= 0 \\ y^2 + y - 1 &= 0 && \REMTEXT{$y = z + \BAR{z}$と置いた} \\ \end{align*} $$テトラ「$y$ の $2$ 次方程式ですね。解くと…… $$ y = \dfrac{-1 \pm \sqrt{5}}{2} $$ になります! 先輩、 $\sqrt{5}$ が出てきましたようっ!」
僕「出てきたね! あれ……プラスマイナス?」
テトラ「プラスマイナスでいいんですよね? $y^2 + y - 1 = 0$ は、 $2$ 次方程式の解の公式を使うと、 $2$ 個の解が出てきて…… $$ \dfrac{-1 + \sqrt{5}}{2} \qquad\REMTEXT{と}\qquad \dfrac{-1 - \sqrt{5}}{2} $$ ……になりますから」
僕「うん、もちろんそれは正しいんだけど、 なぜ $2$ 個になったのかな、と思ったんだよ。 だって、もともと解こうと思ったのは $4$ 次方程式だから $4$ 個の解……あ、違うね、勘違い勘違い。 僕たちが解いたのは $y$ についてだった。 $z + \BAR{z}$ を $y$ と置いたんだから、まだ話は続く」
テトラ「ここまででわかったことは、 $$ z + \BAR{z} = \dfrac{-1 \pm \sqrt{5}}{2} $$ でいいんですよね?」
僕「……」
テトラ「ち、違いました?」
僕「……いやいや、大丈夫。テトラちゃんの理解は正しいよ。 いま僕が考えていたのは、この $2$ 個の解はなんだろうってこと。 つまりこの正 $5$ 角形のどこに出てくるんだろうってね」
テトラ「はあ……」
僕「うん、こうかな。 $z$ は正 $5$ 角形の一つの点……を表す複素数だよね。 そして $\BAR{z}$ はその複素共役になる。 つまり、 $z$ と $\BAR{z}$ は水面に……」
テトラ「あ、はい。《水面に映る星の影》です。 $z$ が星で、 $\BAR{z}$ がその影」
僕「たとえば、正 $5$ 角形の $5$ 個の複素数にこんなふうに名前を付けるとする。 $\zeta_0$(ゼータ $0$)から $\zeta_4$(ゼータ $4$)まで。 そうすると、 $\zeta_1$ の複素共役は $\zeta_4$ にあたるわけだよね」

テトラ「$\zeta_1$ の真下、対称の位置に $\zeta_4$ がありますからそうですね」
僕「うん。そうすると、 $\BAR{\zeta_1} = \zeta_4$ になっている。 $\zeta_1 + \BAR{\zeta_1}$ は $\zeta_1 + \zeta_4$ で、 この和は実数になる。それがさっきの方程式 $y^2 + y - 1 = 0$ の解の一つになるんだ」
テトラ「どうして……共役複素数の和が実数になるっていえるんでしたでしょうか」
僕「だって $a+bi$ と $a-bi$ を加えたら、ちょうど虚部の $bi$ と $-bi$ が打ち消し合うからね」
テトラ「あっ、あたりまえでした。すみません。 ……ということはですよ。さっきの解のうち、 $$ \dfrac{-1 + \sqrt{5}}{2} \qquad\REMTEXT{と}\qquad \dfrac{-1 - \sqrt{5}}{2} $$ のどちらかが、 $\zeta_1 + \BAR{\zeta_1}$ つまり $\zeta_1 + \zeta_4$ になっているということですか」
僕「そうだね。そして、別の方が、 $\zeta_2 + \BAR{\zeta_2}$ つまり $\zeta_2 + \zeta_3$ になってることになる。 そうかそうか。正 $5$ 角形で $1$ を除く頂点は $4$ 個。 その $4$ 個の点は $4$ 個の複素数になっている。 そして、それらは複素共役な $2$ 組のペアになっている。 その $2$ 組のペアと、 $y^2 + y - 1 = 0$ の $2$ 解が対応していたんだ!」
複素共役な $2$ 組の複素数
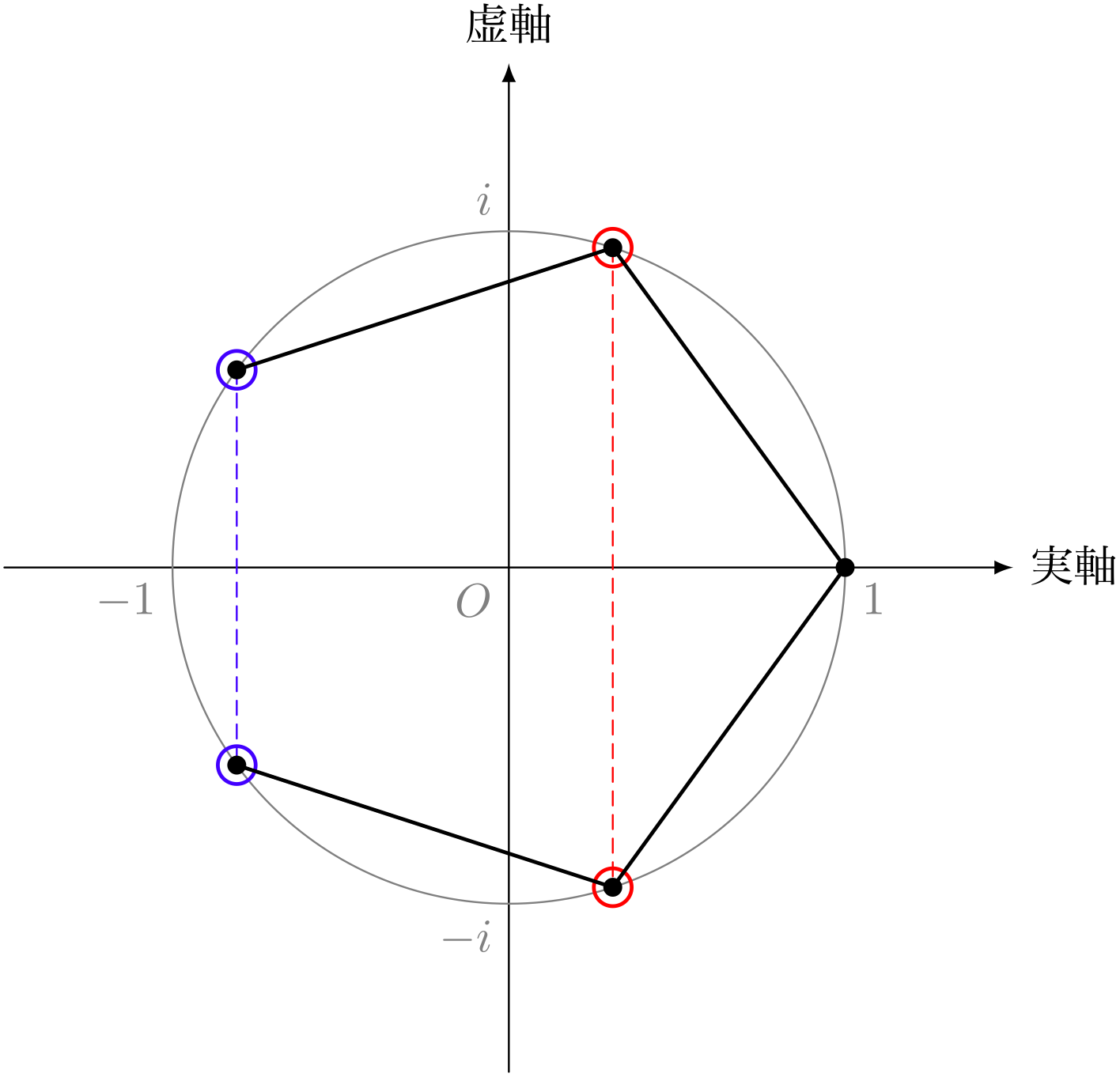
テトラ「共役複素数は、《仲良しペア》ですね!」
僕「ああ、すっきりした。 でも、気がつけばあたりまえだね。だってもともとの $4$ 次方程式の次数を下げたときに使ったのは、 $z + \BAR{z}$ で、あきらかに $2$ 組のペアをまとめて考えようとしていたわけだから」
テトラ「ちょ、ちょっとお待ちください。 部分部分は理解したと思うんですが、大きな流れがわからなくなってしまいました。 整理しますっ!」
僕「$z - 1$ で因数分解、だね」
テトラ「そうでした、そうでした」
僕「$z$ と複素共役な $\BAR{z}$ との積を使って……」
テトラ「$z\BAR{z} = 1$ ですね!」
テトラ「これを解いて、 $$ z + \BAR{z} = \dfrac{-1 \pm \sqrt{5}}{2} $$ が得られたところ、ですね」
僕「うん、複素共役なペアが $2$ 組あって、 $z + \BAR{z}$ の値が $2$ 個ある。 じゃ、どっちがどっちだろうか?」
問題
$2$ 組のペア、 $$ \zeta_1 + \zeta_4 \qquad\REMTEXT{と}\qquad \zeta_2 + \zeta_3 $$ がある。
$2$ 個の数 $$ \dfrac{-1 + \sqrt{5}}{2} \qquad \REMTEXT{と}\qquad \dfrac{-1 - \sqrt{5}}{2} $$ がある。
どっちがどっちだろうか。
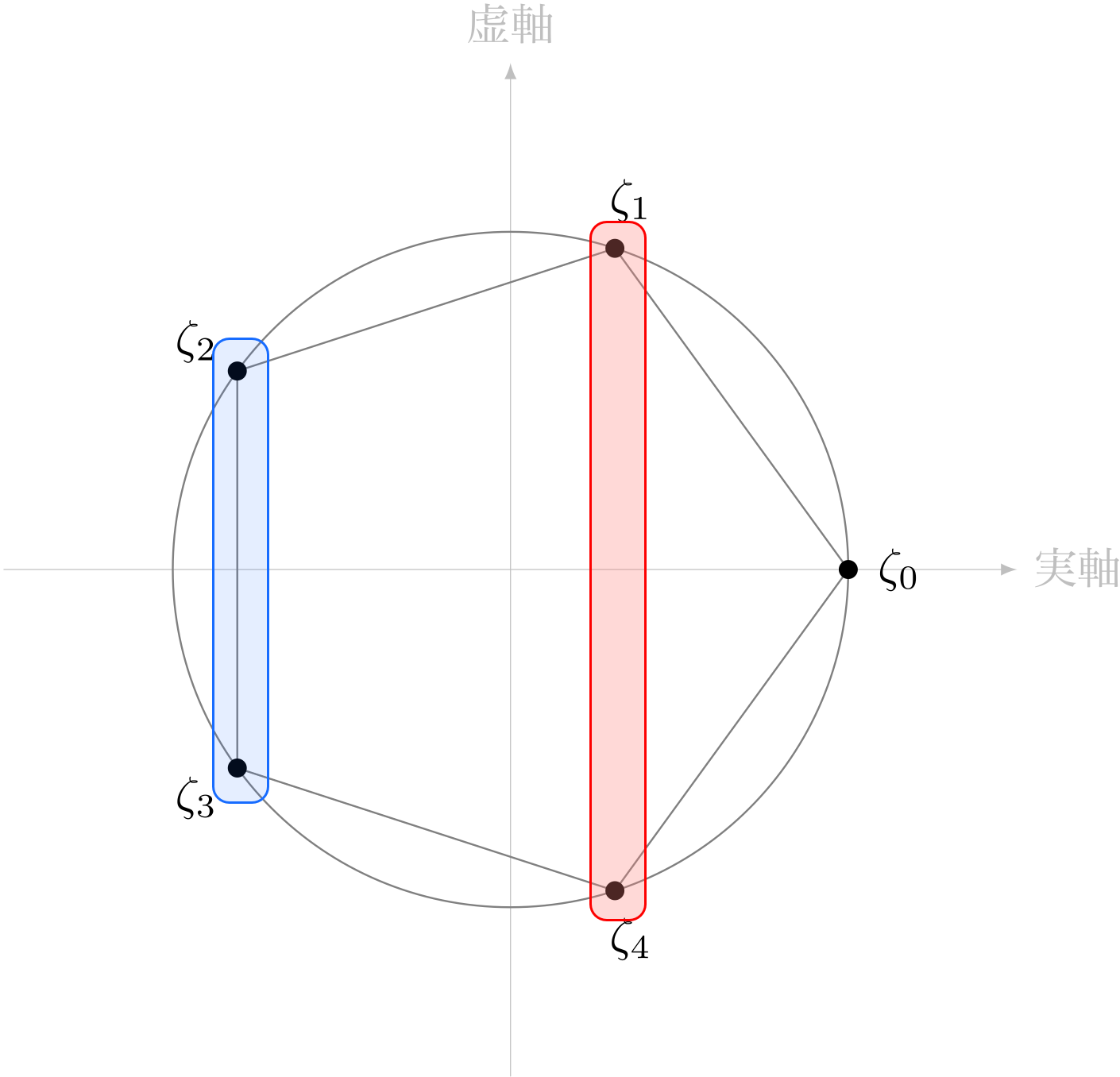

テトラ「可能性は $2$ 通りありますね……」
僕「これはすぐにわかるよ」
テトラ「そうなんですか?」
僕「うん。だって、よく見てみれば、 $$ \dfrac{-1 - \sqrt{5}}{2} < 0 $$ であることがわかるよね。分子が負だから」
テトラ「あっと、そうですね。ということは、 和が負になるペアということで、こうなります」
$$ \zeta_2 + \zeta_3 = \dfrac{-1 - \sqrt{5}}{2} $$僕「そうだね。そして、 $$ \dfrac{-1 + \sqrt{5}}{2} > 0 $$ であることもわかる」
テトラ「はいはい、わかります。 $\sqrt{5}$ は《富士山麓オーム鳴く》で $2.2360679\cdots$ ですから $1$ より大きいです。 なので、 $-1 + \sqrt{5} > 0$ ということですね」
僕「うん、そう。ということで、 $$ \zeta_1 + \zeta_4 = \dfrac{-1 + \sqrt{5}}{2} $$ だとわかった」
解答
複素数のペアと数の対応は、 $$ \left\{\begin{array}{llll} \zeta_1 + \zeta_4 &= \dfrac{-1 + \sqrt{5}}{2} \\ \zeta_2 + \zeta_3 &= \dfrac{-1 - \sqrt{5}}{2} \\ \end{array}\right. $$ となる。

テトラ「何だかおもしろいですね。図形を考えていたら、方程式の話になって、 方程式を考えていたら、複素数の話になって、 複素数を考えていたら、ルートの計算で数の大小の話になって……」
僕「え、でも、そういうのは普通じゃない? だって、方程式を解くときに、数の計算をしたり、式の変形をしたり、 グラフを描いたり、何でもするものだから」
テトラ「そうなんですが……そうですよね。 どんな武器でも使っていいんですよね」
僕「何でも使えるところが、 数学のおもしろいところなんだし」
テトラ「ですねっ!」
僕「さっきの $\zeta_1 + \zeta_4$ と $\zeta_2 + \zeta_3$ は両方ともベクトルの和として考えることもできるね。こんなふうに」
ベクトルの和として $\zeta_1 + \zeta_4$ と $\zeta_2 + \zeta_3$ を考える
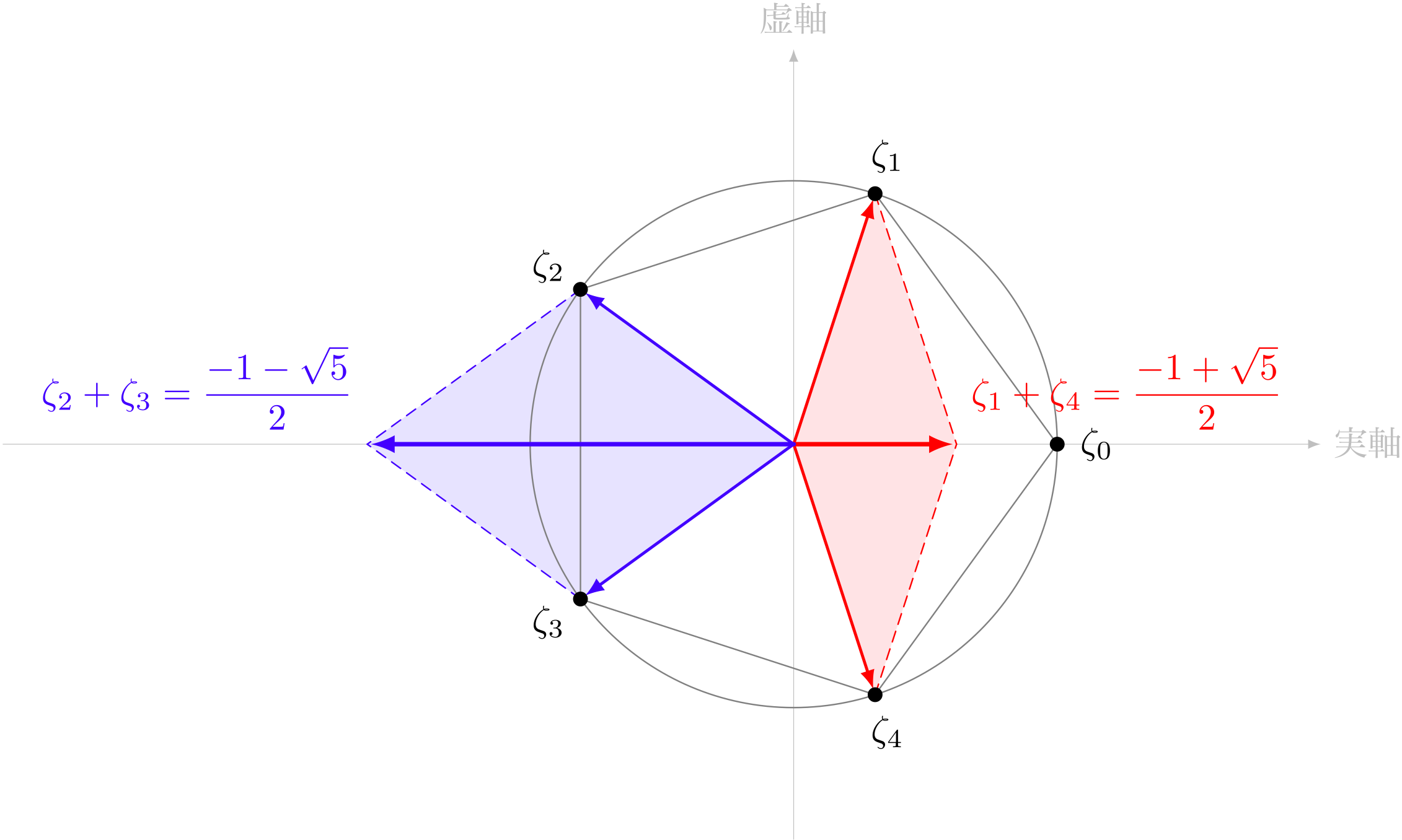
テトラ「ベクトルまで……」
僕「ここまでで、 $$ \zeta_1 + \zeta_4 = \dfrac{-1 + \sqrt{5}}{2} $$ がわかった。 $\BAR{\zeta_1} = \zeta_4$ だから、 $$ \zeta_1 + \BAR{\zeta_1} = \dfrac{-1 + \sqrt{5}}{2} $$ と書いてもいい。ここから $\zeta_1$ を求めることになる。さて?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 420本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2016年8月12日)
この記事は『数学ガールの秘密ノート/複素数の広がり』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!