![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
【CM】今シーズンの話題は『数学ガールの秘密ノート/場合の数』でも詳しく読むことができます。
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
ここは高校の図書室。いまは放課後。
僕とテトラちゃんは、パスカルの三角形と組み合わせの数を数式を使って表していた(第395回参照)。
僕「……さあ、これで組み合わせの数 $\TBINOM n r$ を漸化式で表したことになる」
$\TBINOM n r$ の漸化式
$n$ と $r$ を $0$ 以上の整数とすると、次の式が成り立つ。
$$ \BINOM n r = \begin{cases} 1 & \TEXT{$r = 0$または$n - r = 0$の場合} \\ \DBINOM{n-1}{r-1} + \DBINOM{n-1}{r} & \TEXT{$0 < r < n$の場合} \end{cases} $$
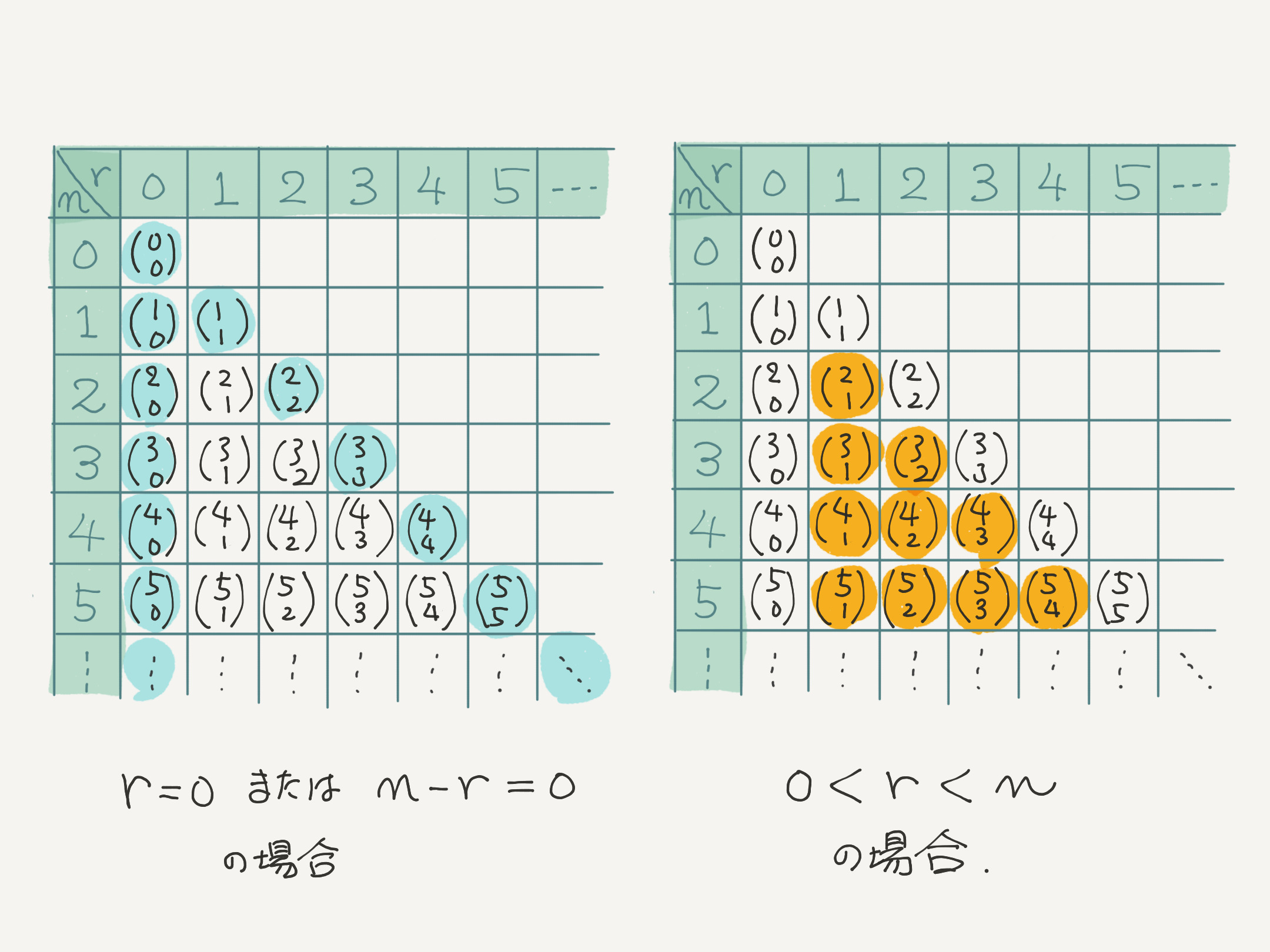
テトラ「$n$ と $r$ の条件を見るだけじゃなくて、 こんなふうに表と照らし合わせて考えると、わかりやすいですね。 そして確かめやすいです!」
僕「だよね。そして $\TBINOM n r$ に出てくる $n$ と $r$ のすべてのケースを《もれなく、だぶりなく》 表していることもはっきりする!」
テトラ「はいはいはいはい! 先輩! 先ほど階乗を使って $\TBINOM n r$ を表しましたから、 あたし、この等式 $$ \BINOM n r = \BINOM{n-1}{r-1} + \BINOM{n-1}{r} $$ が成り立つことを計算で示せると思います! いますぐ計算しますっ!」
僕「おお!」
問題
$n$ と $r$ は整数で $0 < r < n$ とします。このとき、次の等式が成り立つことを証明してください。
$$ \BINOM n r = \BINOM{n-1}{r-1} + \BINOM{n-1}{r} $$
ヒント: $\BINOM n r = \BIFRAC{n!}{r!}{(n-r)!}$

テトラ「あたしの計算方針はこうです。証明したい式の右辺、つまり、これを計算しちゃうんです。 これを計算した結果が $\BINOM n r$ に等しくなればいいんですよね?」
$$ \begin{align*} \BINOM{n-1}{r-1} + \BINOM{n-1}{r} &= \TEXT{?} \end{align*} $$僕「そうだね。その通り」
テトラ「あたしはもう $\BINOM{n-1}{r-1}$ と $\BINOM{n-1}{r}$ を階乗を使って書くことができますから、 二つの分数の和を計算すればいいはずです。 も、文字がたくさん出てきますけれど、きっとうまいこと計算できるはず……と信じて進みます」
僕「うんうん」
テトラ「まず、 $\BINOM{n-1}{r-1}$ と $\BINOM{n-1}{r}$ をそれぞれ階乗を使って書きます」 $$ \begin{align*} \BINOM{n-1}{r-1} &= \BIFRAC{(n-1)!}{(r-1)!}{(n-1-(r-1))!} && \REMTEXT{階乗で表した} \\ &= \BIFRAC{(n-1)!}{(r-1)!}{(n\CANCEL{{}-1}- r\CANCEL{{}+1})!} && \REMTEXT{内側のカッコを外した} \\ &= \BIFRAC{(n-1)!}{(r-1)!}{(n-r)!} && \REMTEXT{整理した} \\ \BINOM{n-1}{r} &= \BIFRAC{(n-1)!}{r!}{(n-1-r)!} && \REMTEXT{階乗で表した} \\ &= \BIFRAC{(n-1)!}{r!}{(n-r-1)!} && \REMTEXT{整理した} \\ \end{align*} $$
僕「サクサク進むねえ」
テトラ「計算はサクサク進むんですが、目はチカチカします。 $n$ と $r$ と $1$ が飛び交ってますっ!」
僕「あはは」
テトラ「そして、この二つの分数を足すんですが、もちろん通分することになりますよね。 何かを掛けて、分母を揃えます。 さて何を掛けるかというと……」
$$ \begin{align*} \BINOM{n-1}{r-1} + \BINOM{n-1}{r} &= \BIFRAC{(n-1)!}{(r-1)!}{(n-r)!} + \BIFRAC{(n-1)!}{r!}{(n-r-1)!} \\ &= \REMTEXT{通分したい……} \end{align*} $$僕「……」
テトラ「あ、たぶん見えましたよ……ええとですね、 こっちには $\MARKB{r}$ を掛けて、そっちには $\MARKA{n-r}$ を掛ければいいんでしょうか?」
$$ \BIFRAC{(n-1)!}{\MARKB{(r-1)!}}{(n-r)!} + \BIFRAC{(n-1)!}{r!}{\MARKA{(n-r-1)!}} $$僕「きっとそうだよ。どれが『こっち』でどれが『そっち』かわからないけど」
テトラ「はい。『こっち』は $\MARKB{(r-1)!}$ です。 だって、 $r$ を $(r-1)!$ に掛けると $r!$ になりますから。 階乗ってそういうものですっ!」
$$ \begin{align*} r \times \MARKB{(r-1)!} &= r \times (\MARKB{(r-1)\times(r-2)\times\cdots\times2\times1}) \\ &= r \times (r-1)\times(r-2)\times\cdots\times2\times1 \\ &= r! \end{align*} $$僕「そうだね。 $r$ が $(r-1)!$ の先頭に吸い込まれたみたいだ」
テトラ「ほんとですね……それから、同じように $n-r$ を $(n-r-1)!$ に掛けると $(n-r)!$ になります」
$$ \begin{align*} (n-r) \times \MARKA{(n-r-1)!} &= (n-r) \times (\MARKA{(n-r-1)\times(n-r-2)\times\cdots\times2\times1}) \\ &= (n-r) \times (n-r-1)\times(n-r-2)\times\cdots\times2\times1 \\ &= (n-r)! \end{align*} $$僕「これで通分ができるね」
テトラ「はいはい、計算が進みますっ!」
$$ \begin{align*} & \BINOM{n-1}{r-1} + \BINOM{n-1}{r} \\ &= \BIFRAC{(n-1)!}{(r-1)!}{(n-r)!} + \BIFRAC{(n-1)!}{r!}{(n-r-1)!} \\ &= \BIFRAC{\MARKB{r}(n-1)!}{\MARKB{r}(r-1)!}{(n-r)!} + \BIFRAC{\MARKA{(n-r)}(n-1)!}{r!}{\MARKA{(n-r)}(n-r-1)!} \qquad \REMTEXT{分母を揃えている途中です} \\ &= \frac{\MARKB{r}(n-1)!}{\MARKC{r!\SP(n-r)!}} + \frac{\MARKA{(n-r)}(n-1)!}{\MARKC{r!\SP(n-r)!}} \qquad \REMTEXT{分母が揃いました!} \\ &= \BIFRAC{r(n-1)! + (n-r)(n-1)!}{r!}{(n-r)!} \qquad \REMTEXT{分子同士の和にできました} \\ &= \BIFRAC{r\MARKA{(n-1)!} + (n-r)\MARKA{(n-1)!}}{r!}{(n-r)!} \qquad \REMTEXT{$\MARKA{(n-1)!}$でくくれそう……} \\ &= \BIFRAC{(r + (n-r))\MARKA{(n-1)!}}{r!}{(n-r)!} \qquad \REMTEXT{$\MARKA{(n-1)!}$でくくりました} \\ &= \BIFRAC{(\CANCEL{r} + n \CANCEL{{}-r})(n-1)!}{r!}{(n-r)!} \qquad \REMTEXT{計算を進めて……} \\ &= \BIFRAC{n (n-1)!}{r!}{(n-r)!} \qquad \REMTEXT{計算を進めて……} \\ &= \BIFRAC{n!}{r!}{(n-r)!} \qquad \REMTEXT{ようやく……} \\ &= \BINOM n r \qquad \REMTEXT{できましたっ!} \end{align*} $$僕「できたね!」
テトラ「はいっ! 何とかめげずに計算できましたっ!」
解答(テトラちゃんの証明)
$\BINOM{n-1}{r-1} + \BINOM{n-1}{r}$ を階乗を使った式に直して計算します。 $$ \begin{align*} \BINOM{n-1}{r-1} + \BINOM{n-1}{r} &= \BIFRAC{(n-1)!}{(r-1)!}{(n-r)!} + \BIFRAC{(n-1)!}{r!}{(n-r-1)!} \\ &= \BIFRAC{r(n-1)! + (n-r)(n-1)!}{r!}{(n-r)!} \\ &= \BIFRAC{n!}{r!}{(n-r)!} \\ &= \BINOM n r \end{align*} $$ したがって、 $$ \BINOM n r = \BINOM{n-1}{r-1} + \BINOM{n-1}{r} $$ が成り立ちます。 (証明終わり)
僕「何だか、いつものテトラちゃんじゃないみたいだ……」
テトラ「はい?」
僕「あっ、ごめん! これじゃ僕は一点減点になってしまう(第394回参照)」
テトラ「すみません、何のお話ですか?」
僕「いやあ、いつものテトラちゃんだったら文字が飛び交うのを嫌がるけど、 今日はてきぱき進むなあと思ったんだよ。 でもそれを『いつものテトラちゃん』って決めつけるのは良くないよね」
テトラ「ああ、そういうことですか。 でも、今回の《てきぱきテトラ》には不安解消の秘密兵器があるんです」
僕「秘密兵器って?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 420本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2023年6月16日)