![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕は高校生。今日は中学生のいとこ、ユーリといっしょに双倉図書館(ならびくらとしょかん)で開催されているイベントにやってきた。
イベントは《いにしえの数学》という企画で、
さまざまな国の、古い時代の数学についてパネル展示がなされている。
しかし、それだけではない。あちこちのパネルには関連する数学の問題が掲示されていて、
実際に数学を楽しめるようになっているのだ。
もちろん、ミルカさんやテトラちゃんもいっしょに来ているのだが……
ユーリ「お兄ちゃん、早く早く! たっくさんパネルがあるから、全部まわるのに時間足りなくなるよ! ほら、は・や・く!」
僕「ちょっと待った、ユーリ。……ほら、ミルカさんやテトラちゃんとはぐれてしまったじゃないか。いったんエントランスまで戻ろうよ」
ユーリ「だーいじょぶだって。またすぐ会えるって。それより、ねーねー、どれから見る? 《いしにえの数学》だって」
僕「《いしにえ》じゃなくて《いにしえ》だよ。《古い》という意味だね」
ユーリ「いにしえ」
僕「順番に見ていけばいいんじゃない? ええと、ここは《古代エジプト》のコーナーだなあ」
ユーリ「これが、古代エジプトの数字?」
僕「そうみたいだね」
古代エジプトの数字($1$ から $10$)
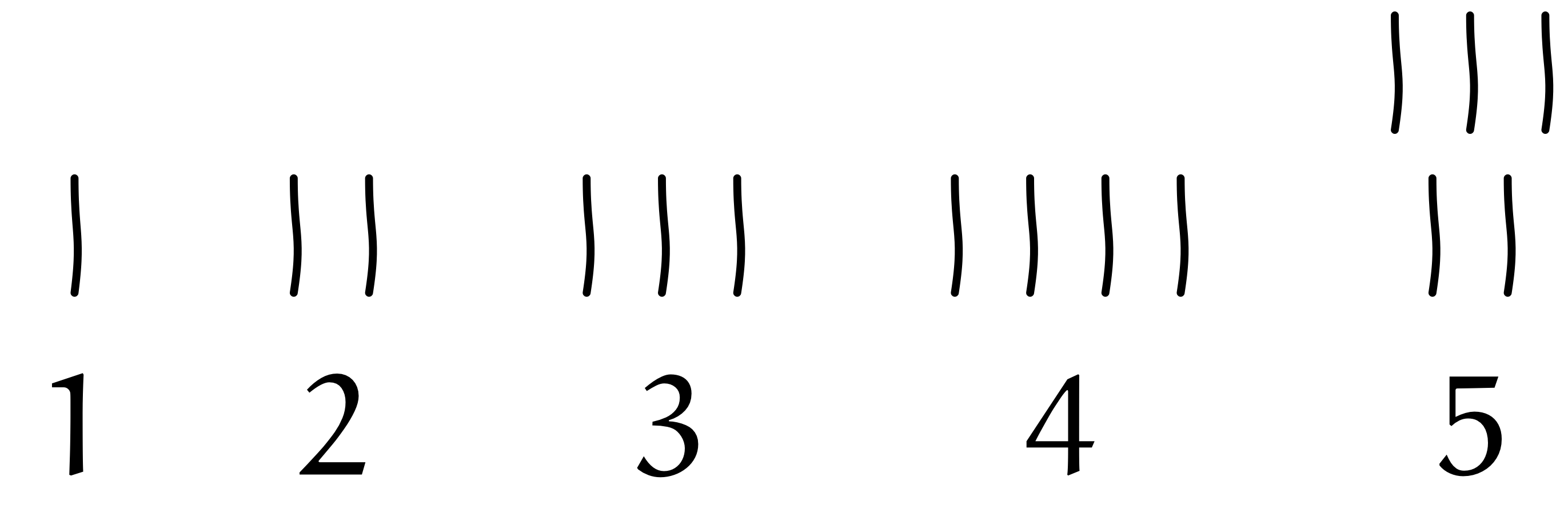
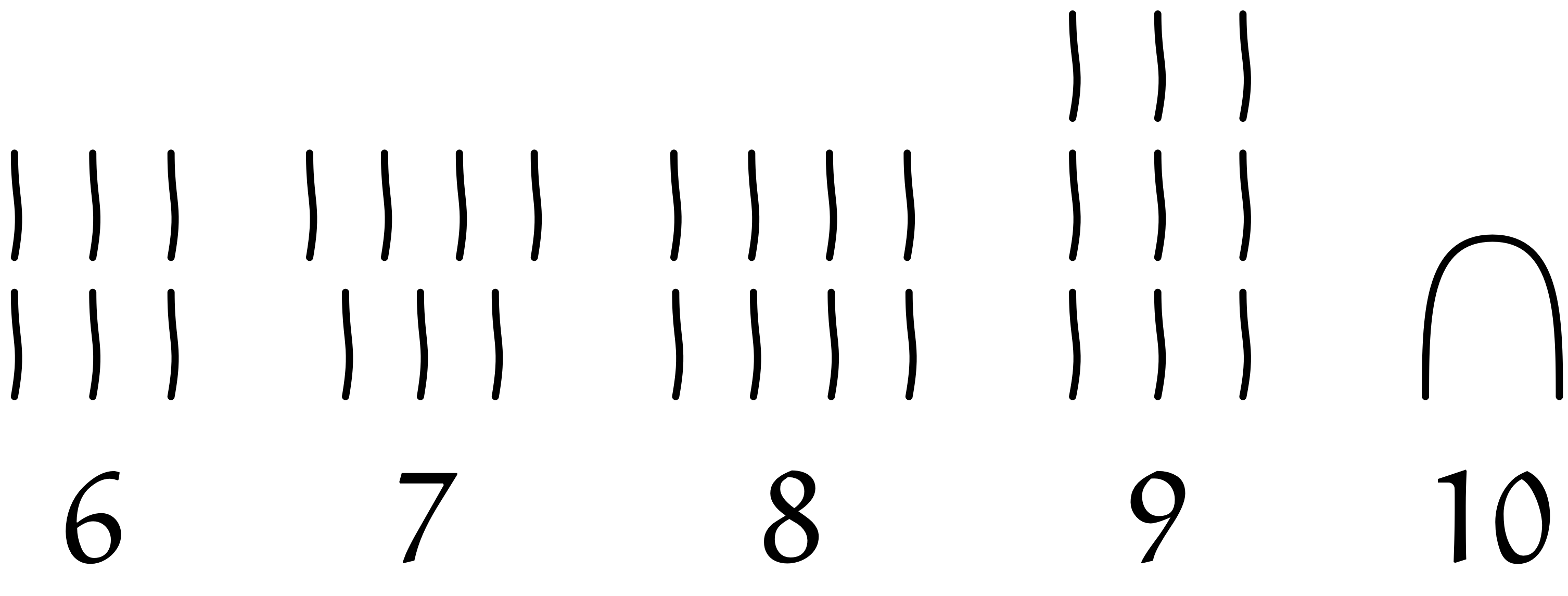
※注:ここで使用している文字はヒエログリフ(聖刻文字、神聖文字)です。
ユーリ「ふーん。じゃ、次のパネル行こっか」
僕「いやいや、『行こっか』じゃないよ。これおもしろいね」
ユーリ「何がおもしろいの? だって、《数のまんま》じゃん。 $1$ は一本の線で、 $2$ は二本の線」
僕「僕たちはふだん、 $1,2,3,4,5,6,7,8,9$ のように別の数に別の数字をあてはめているよね。 たとえば『$3$』という一文字で三という数を表している。 でも、この古代エジプトの……ええと、ヒエログリフでは、違う。 棒の本数を使って数を表しているんだね」
ユーリ「まーね。日本語の漢字だと『三』という三本線で『三』を表してるけどね」
僕「ああ、まあ、そうか……」
ユーリ「とにかく、《線の本数》で数を表しているんだから、やっぱり《数のまんま》じゃないの?」
僕「そうなんだけど、 $10$ になると、線が十本あるんじゃなくて、曲がった線一本になってるよね。 だから $10$ の《まとまり》を一つのものだと思ってるんだ。 ええと……説明によると、卵が $10$ 個入る《かご》があって、《かごの取っ手》で $10$ を表しているんだって。なるほど」
ユーリ「へー……次のパネルに行こうよ!」
古代エジプトの数字($10$ から $20$)


僕「なるほどね。書き並べるだけで、合計した数を表していることになるんだね」
ユーリ「それって、《あたりまえ》ではないでしょーか」
僕「いやいや、それほど《あたりまえ》じゃないよ、ユーリ。だって、僕たちが使っている数は違うよね。 $1$ と $2$ を並べて書いたら、 合計した $3$ を表していることになる?」
ユーリ「そっか。 $1$ と $2$ を並べたら『十二』になっちゃうか……」
僕「こっちのパネルには、もっと大きな数が書いてあるよ」
古代エジプトの数字($100,1000,10000$)

ユーリ「$100$ は渦巻きみたい」
僕「$100$ はぐるぐるとたくさん《巻いたロープ》で、 $1000$ はナイル川のほとりにたくさん咲いている《ハスの花》。 それから、 $10000$ はナイル川のほとりにたくさん生えている《葦またはパピルス草の芽》という説明があるね」
ユーリ「ナイル川の話ばっかりや」
僕「エジプトはナイル川なしには語れないから」
ユーリ「《巻いたロープ》でも《ハスの花》でも、たくさん集まってるものをひとつ描いて、たくさんの数を表すってこと?」
僕「そうみたいだね。 $100000$ はたくさん集まっている《おたまじゃくし》で、 $1000000$ は、たくさんの星空を《仰ぎ見る姿》だって。 そうか! $10$ 倍するごとに《まとまり》になるという点では、十進法だといえるね」
ユーリ「ふんふん。あ、クイズがあるよ」
クイズ(古代エジプトの数)
ヒエログリフを使って、 $$ 12345(一万二千三百四十五) $$ を書き表してみましょう。

僕「できた?」
ユーリ「カンタンカンタン!」
クイズの答え(古代エジプトの数)
ヒエログリフを使って、 $$ 12345(一万二千三百四十五) $$ を書き表すと、たとえば、
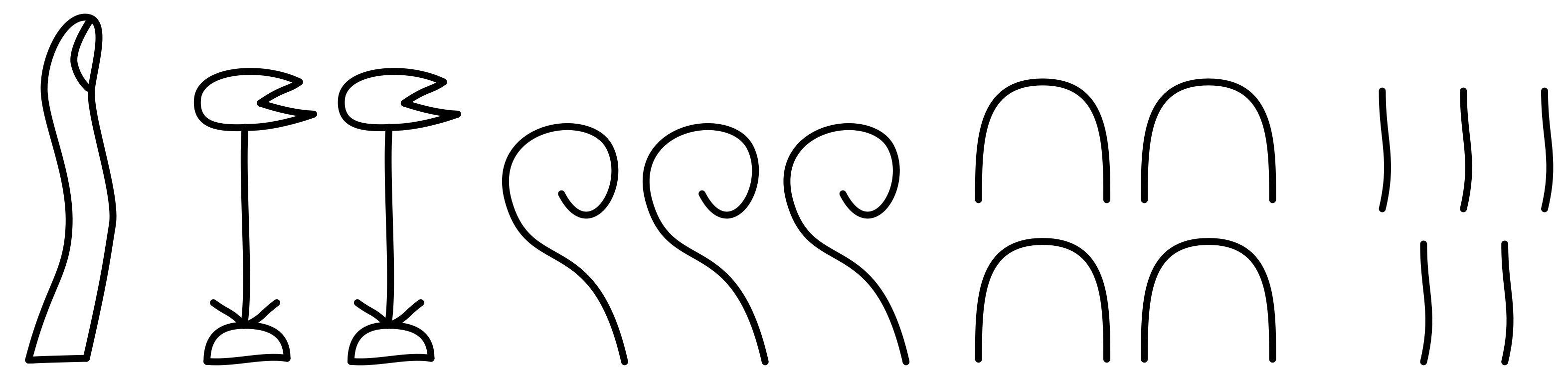
のようになります。
僕「パネルの説明によると、右から左に並べる場合もあるし、 左から右に並べる場合もあるみたいだね。文字そのものが数の大きさを表しているから、 順番が変わっても表す数は変わらないんだ。僕たちの書き方では《位取り記数法》だから、場所が変わったらたいへんだね」
ユーリ「$12$ と $21$ は違う」
僕「そういうこと、そういうこと。そうか。《十進法》であることと《位取り記数法》は独立した話か……」
ユーリ「ねーねー、こっちにもクイズのパネルがあるよ」
クイズ(古代エジプトの数)
以下のヒエログリフは、どんな数を表しているでしょうか。
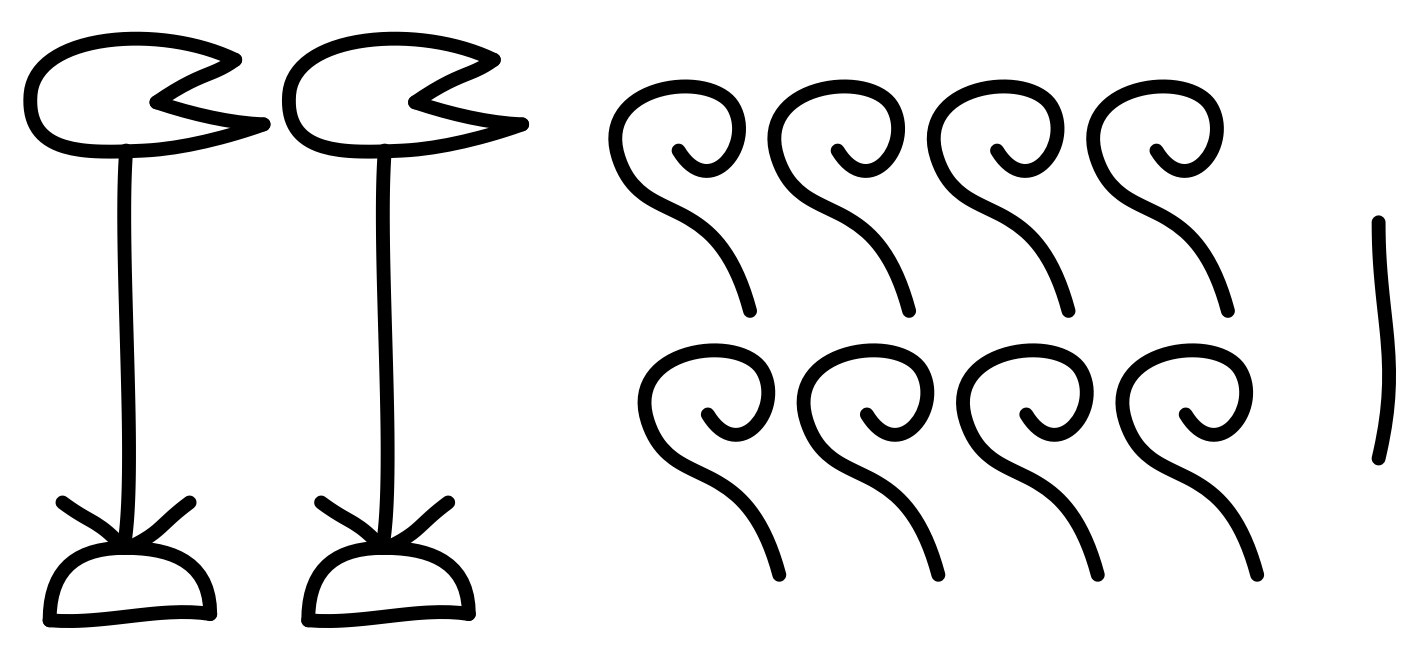

僕「なるほどね……」
ユーリ「なにがなるほどなの? $2801$ でしょ? 《ハスの花》が $1000$ で、《巻いたロープ》が $100$ で、《線》が $1$ だから」
クイズの答え(古代エジプトの数)
以下のヒエログリフは、 $2801$ という数を表しています。
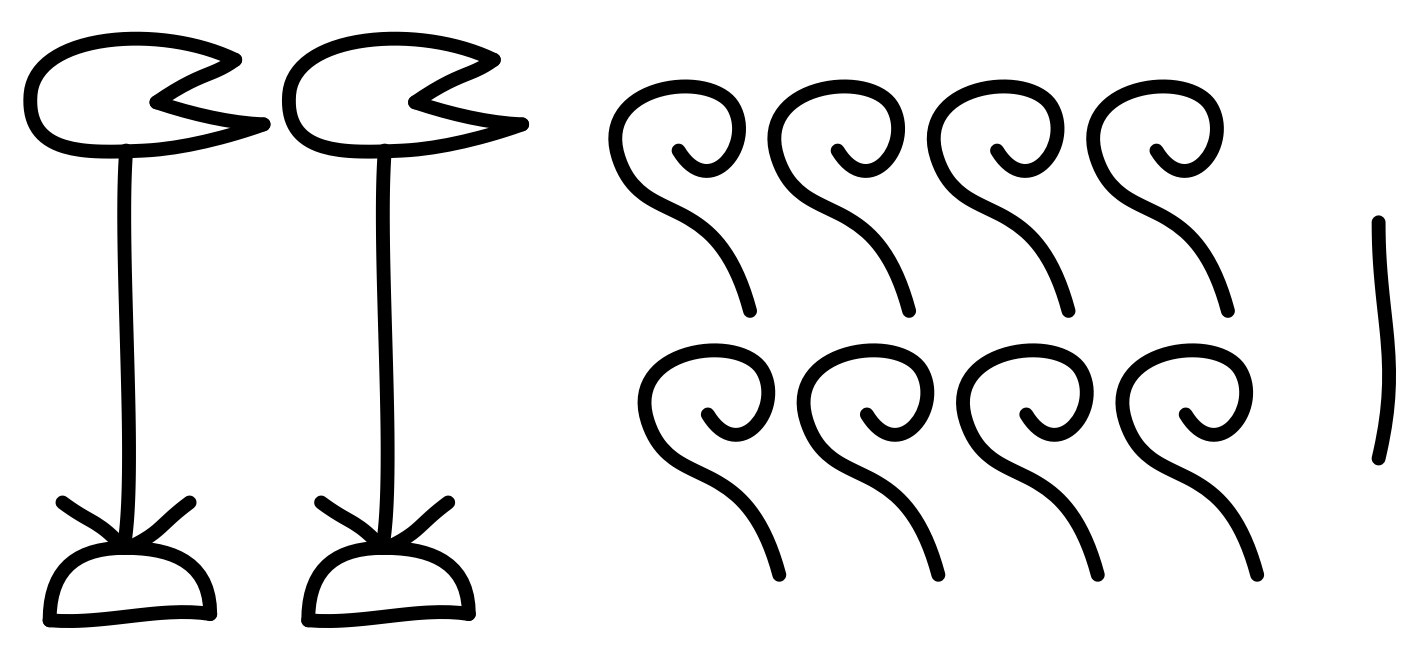
僕「うん、それでいいんだけどね。ほら、 $2801$ には $0$ が出てくる。十の位」
ユーリ「そだね」
僕「でも、さっきのクイズでは、十の位が現れない。《かごの取っ手》は出てこないよね」
ユーリ「だって、 $10$ は《ない》もん。あたりまえでは?」
僕「$2801$ と書いたときには $0$ が《ある》よね。そこがおもしろい」
ユーリ「むー……」
ユーリ「それはさておき、古代エジプトだと《足し算》はすぐできるね、お兄ちゃん。だって、数を並べればいーんでしょ?」
$2 + 3 = 5$
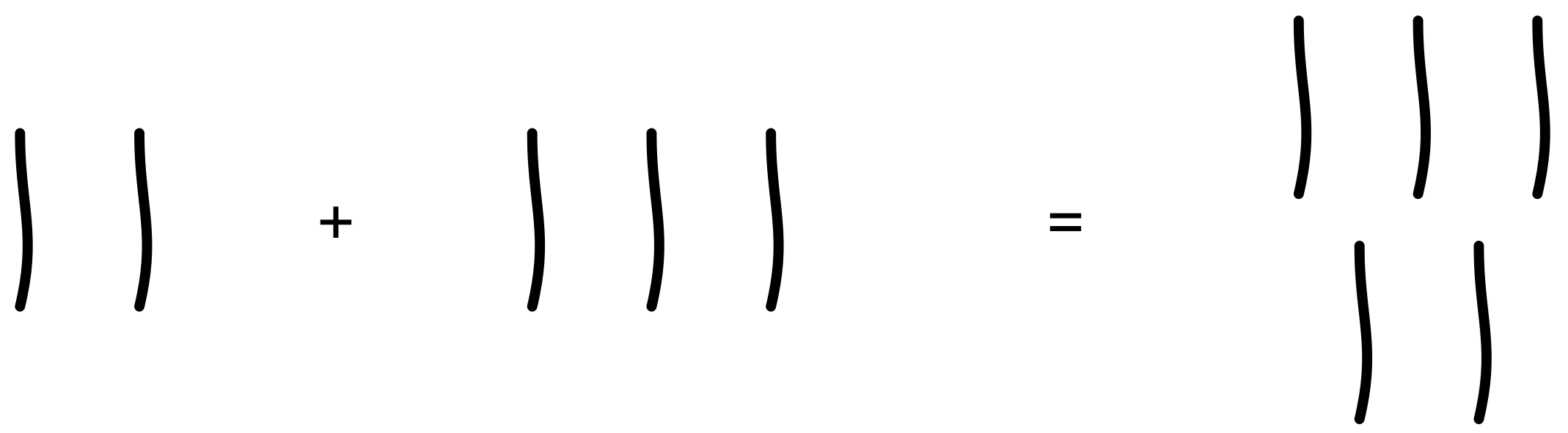
僕「確かにそうなるね……ああ、でも、繰り上がりの代わりに数字を書き換える必要はあるかも。 $5+5 = 10$ になったら《線が $10$ 本》を《かごの取っ手 $1$ 個》にするみたいに」
$5 + 5 = 10$
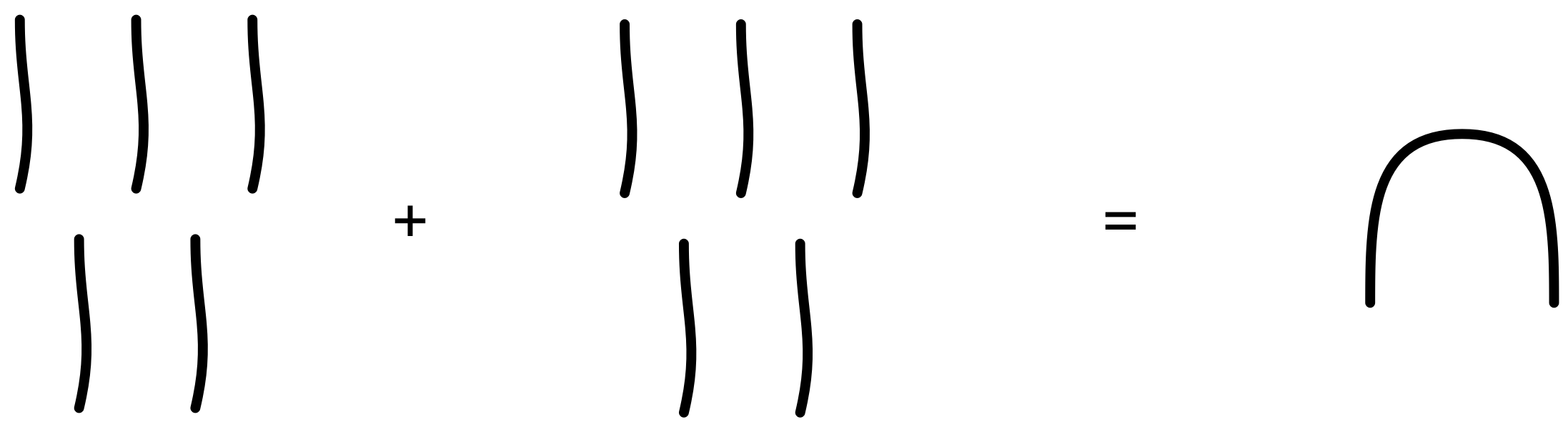
ユーリ「ふんふん……」
僕「足し算はいいとして、古代エジプトの数字を使った《掛け算》はたいへんそうだな……どうやるんだろう」
ユーリ「九九みたいなのがあったりして。《かごの取っ手》掛ける《巻いたロープ》イコール《ハスの花》みたいに」
僕「あっちに掛け算の説明パネルがあるよ。見にいこう」
ユーリ「うん!」
クイズ(古代エジプトの掛け算)
以下の図は、古代エジプトの掛け算($2801 \times 7$)のようすを表しています。 どのようにして答えを求めたのか、考えてみましょう。
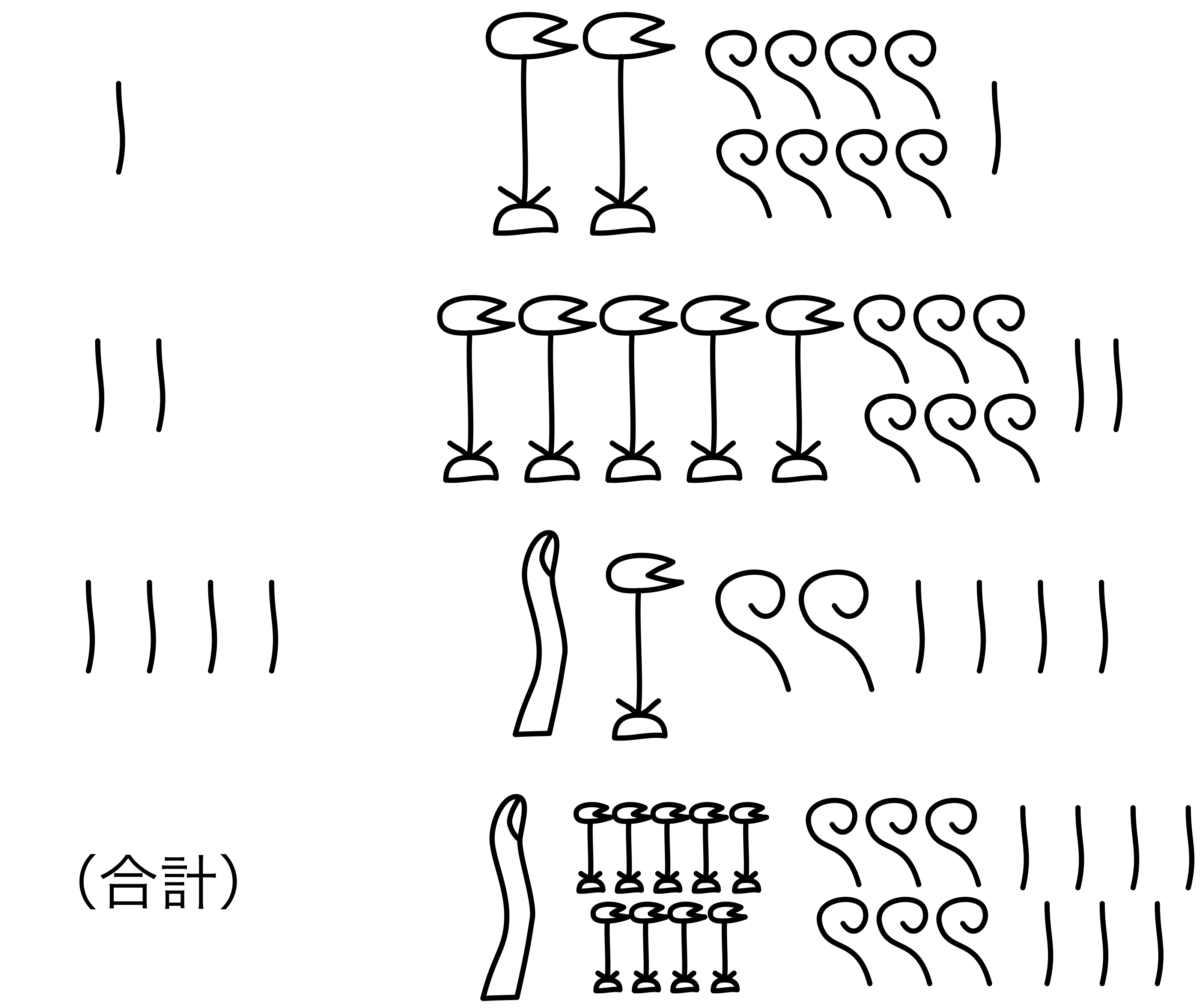
※このクイズは、リンドパピルスに登場する問題79をもとにしています。
ユーリ「説明パネルじゃないよ。これもクイズじゃん!」

(双倉図書館の館内放送)
↑のクイズは、今回の記事でとても大切です。
あわてて先に進まずに、ちょっと立ち止まって考えてくださいね。
ユーリ「(いまの館内放送、なに?)」
僕「(まあいいから。たぶんメタな介入があったんだよ)ともかく、このクイズ、このままだと考えにくいなあ……」
ユーリ「だよねー」
僕「うん、そうだ。いったんアラビア数字と位取り記数法に直してみよう! その方が読みやすいし」
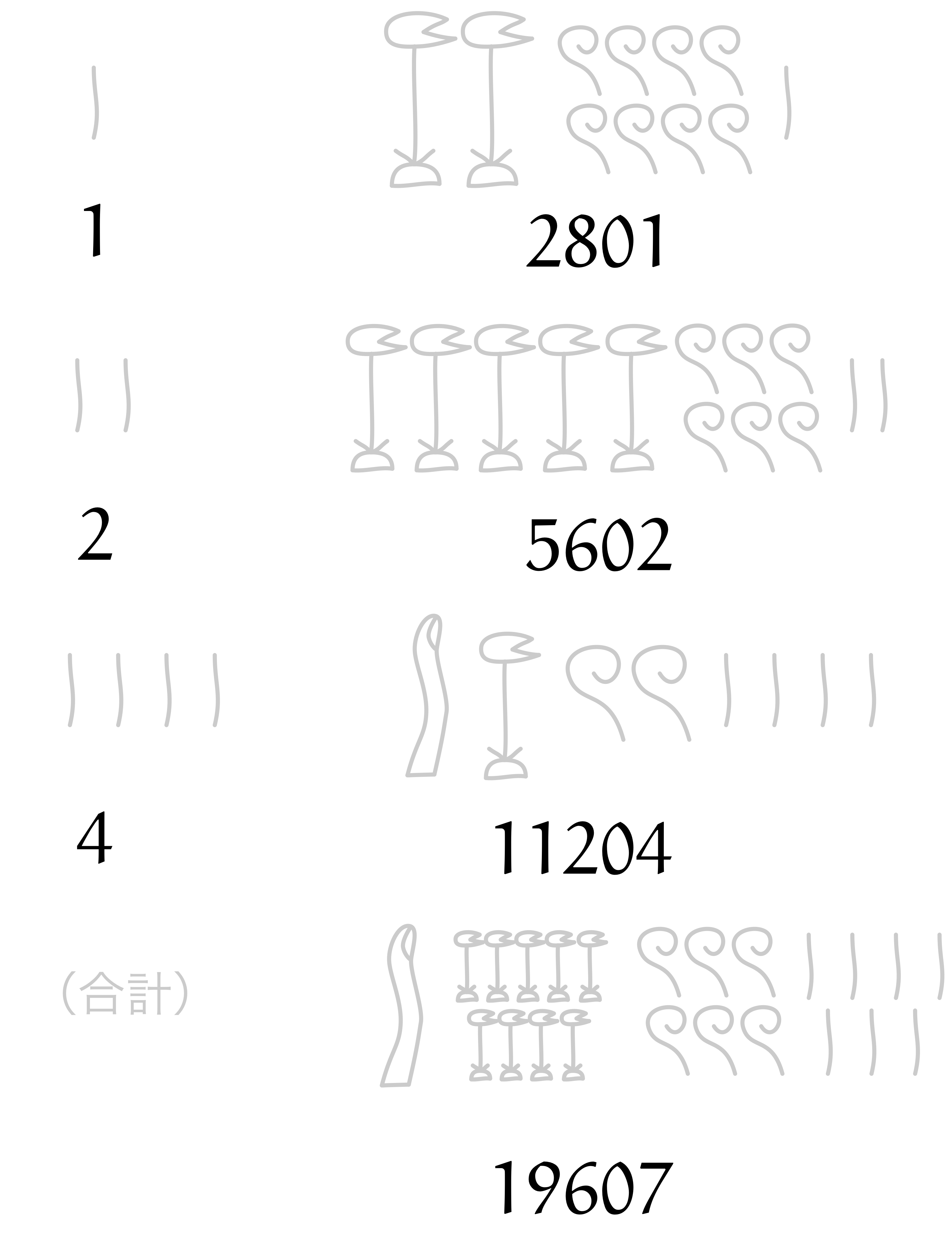
ユーリ「ねーねー、お兄ちゃん。ひえろぐりふ、もう関係なくない?」
僕「そうだね。じゃあ、数字だけまとめてみようか」

ユーリ「あっ、わかった! $2$ 倍してるんだよ!」
僕「そうだね。左の列は $1,2,4$ になっているから、上の数を毎回 $2$ 倍している。 右の列は $2801,5602,11204$ だからこれも、上の数を毎回 $2$ 倍している。 言い換えると、 $2801 \times 1$ と、 $2801 \times 2$ と、 $2801 \times 4$ を計算していることになる」
ユーリ「待ってよ。これって $2801 \times 7$ の掛け算じゃなかったっけ。 $2$ 倍を繰り返すだけで、掛け算できるの?」
僕「最後に、 $2801$ と $5602$ と $11204$ を合計しているよ。それで、確かに $2801 \times 7 = 19607$ が求められてるけど……」
ユーリ「うーん……」
僕「そうか! $7 = 1+2+4$ だから確かに計算が合う。つまり、こういうこと」
$$ \begin{align*} & 2801 \times 7 && \REMTEXT{これを計算したい} \\ &= 2801 \times (1 + 2 + 4) && \REMTEXT{$7 = 1 + 2 + 4$だから} \\ &= (2801 \times 1) + (2801 \times 2) + (2801 \times 4) && \REMTEXT{分配法則を使った} \\ &= 2801 + 5602 + 11204 && \REMTEXT{乗算を行った} \\ &= 19607 && \REMTEXT{すべてを合計した} \\ \end{align*} $$
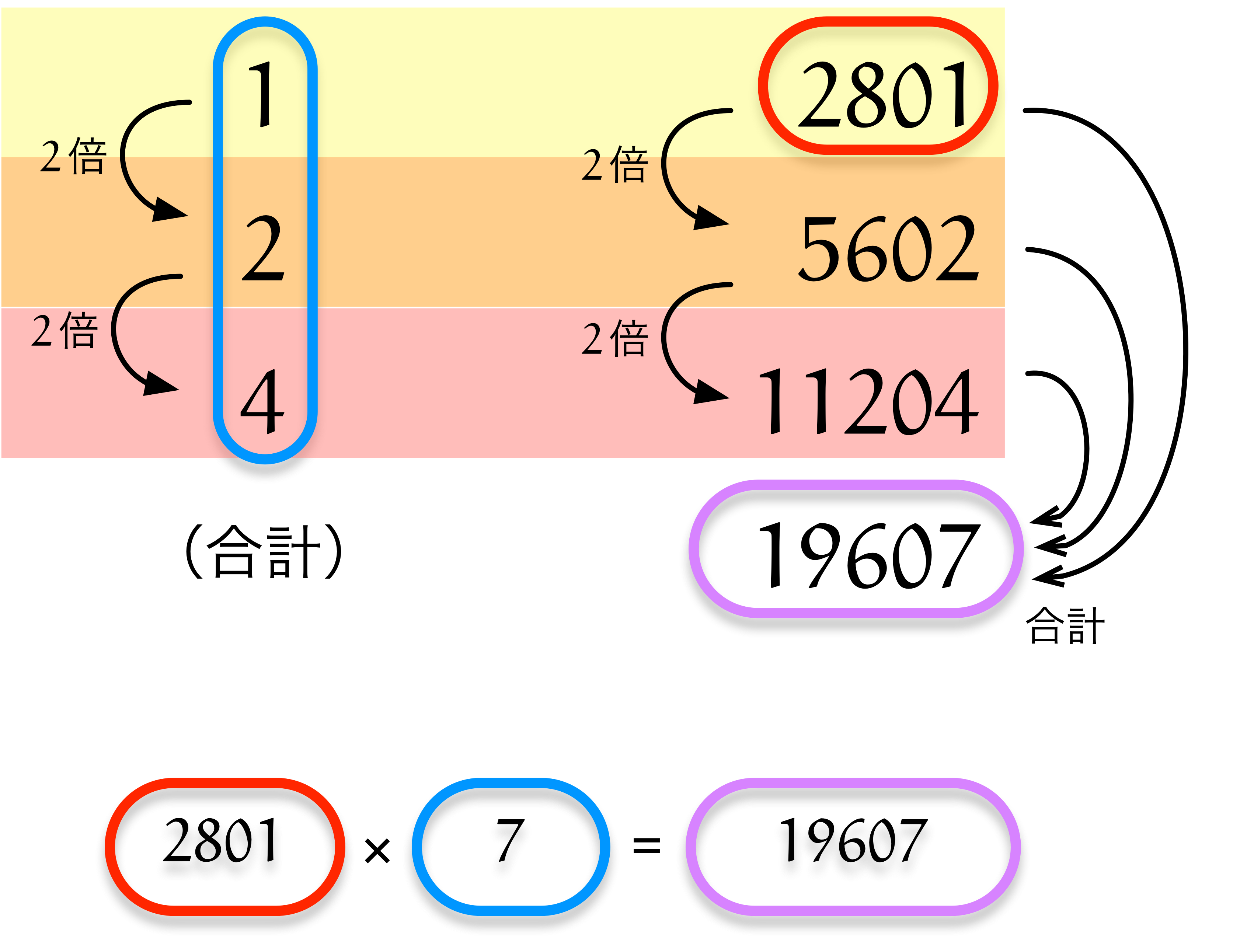
ユーリ「ほほー……にゃるほどね。 $2801$ を、 $1$ 倍したのと $2$ 倍したのと $4$ 倍したのを足すと、 $2801$ を $7$ 倍したものになるってこと?」
僕「そういうことだね」
ユーリ「こっちに別のクイズがあるよ」
クイズ(古代エジプトの掛け算)
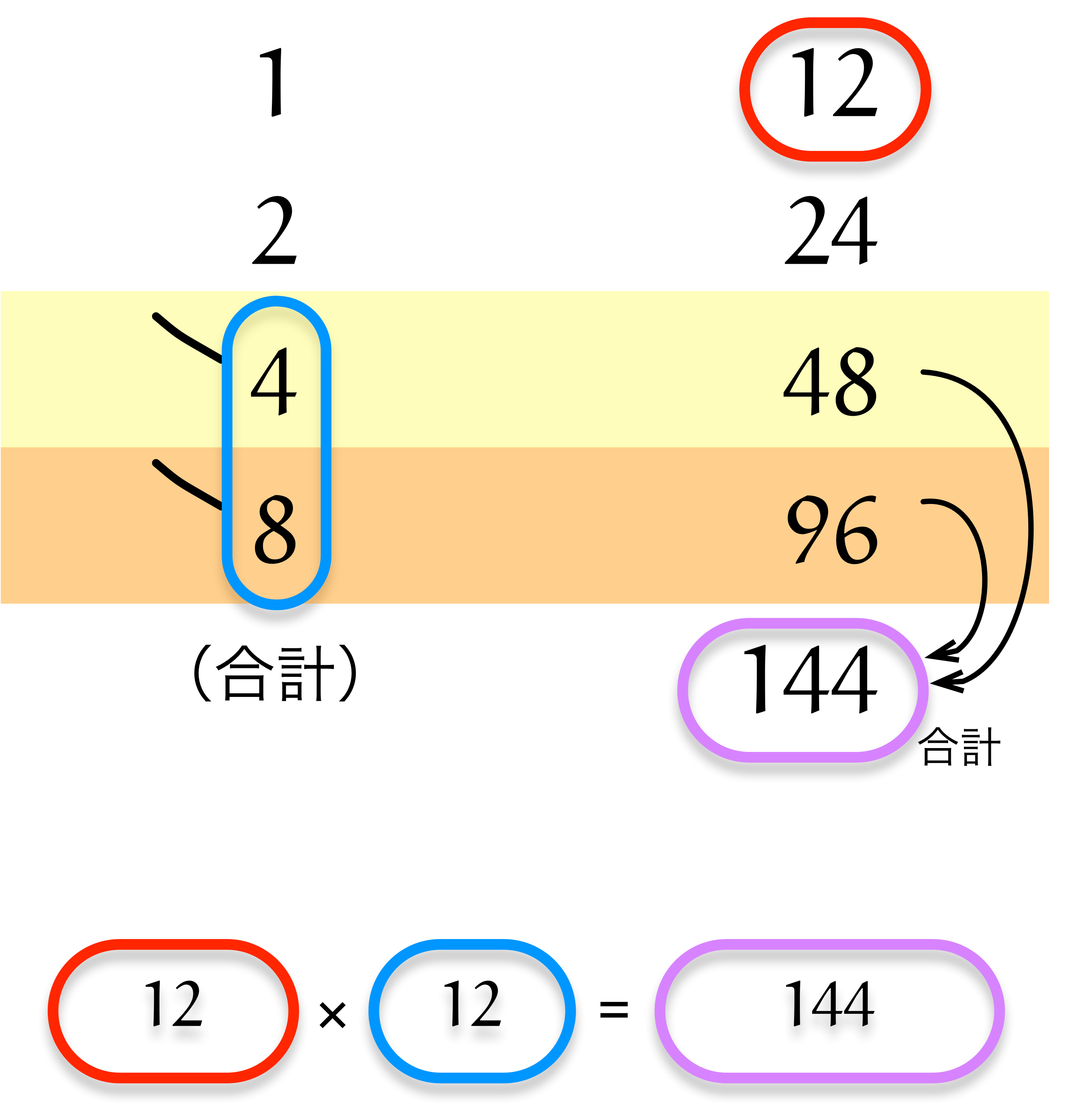
以下の図は、古代エジプトの掛け算($12 \times 12$)のようすを表しています。 どのようにして答えを求めたのか、考えてみましょう。

※このクイズは、リンドパピルスに登場する問題32をもとにしています。

ユーリ「やり方わかったから、すぐできそー!」
僕「……待って。 $4$ と $8$ のところに印がついてる」
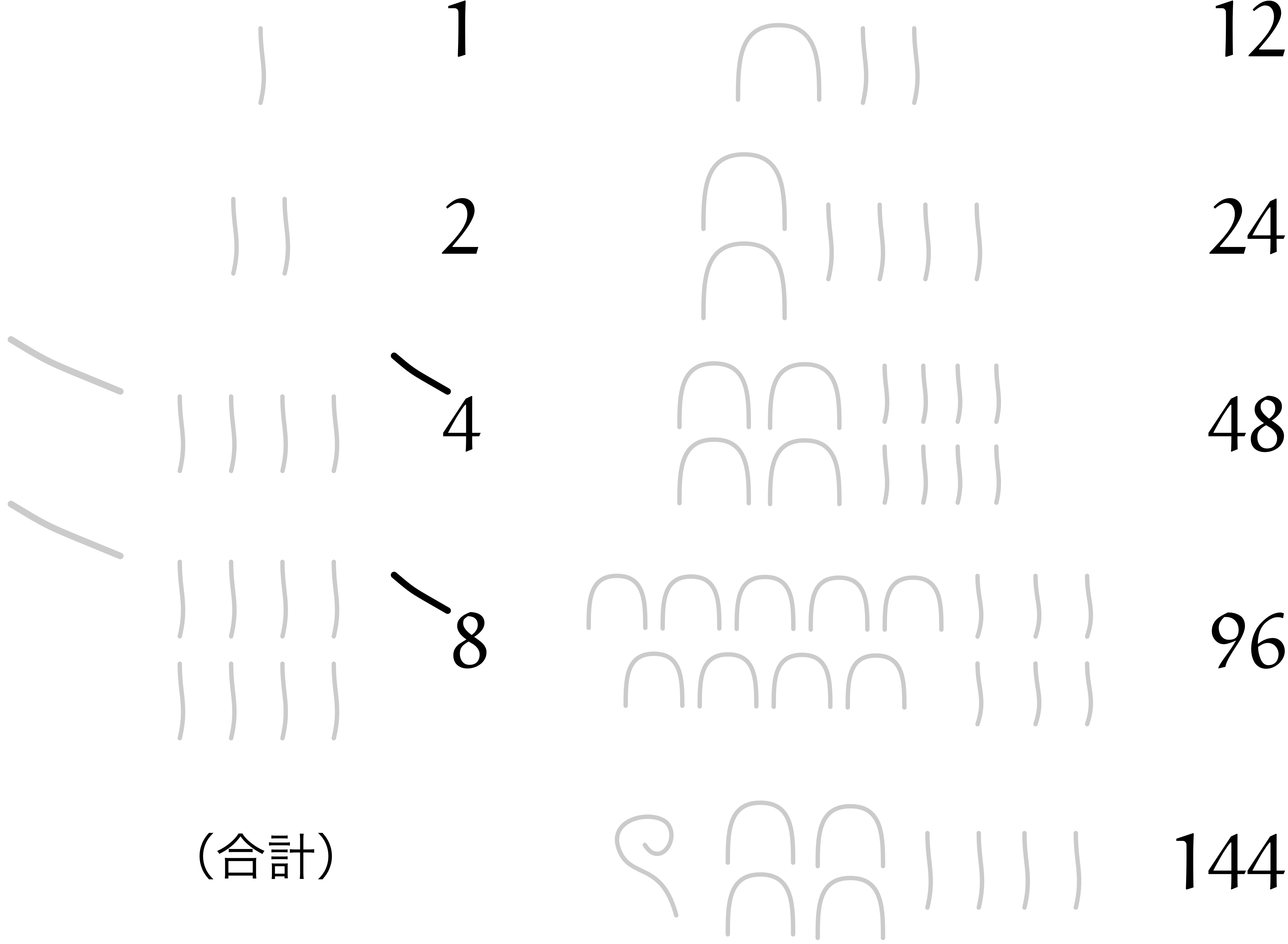
ユーリ「\ $4$ と\ $8$ のこと? これ、マイナス?」
僕「いや、そんなわけはないね。 $12 \times 12$ に必要な印なんだよ、きっと」
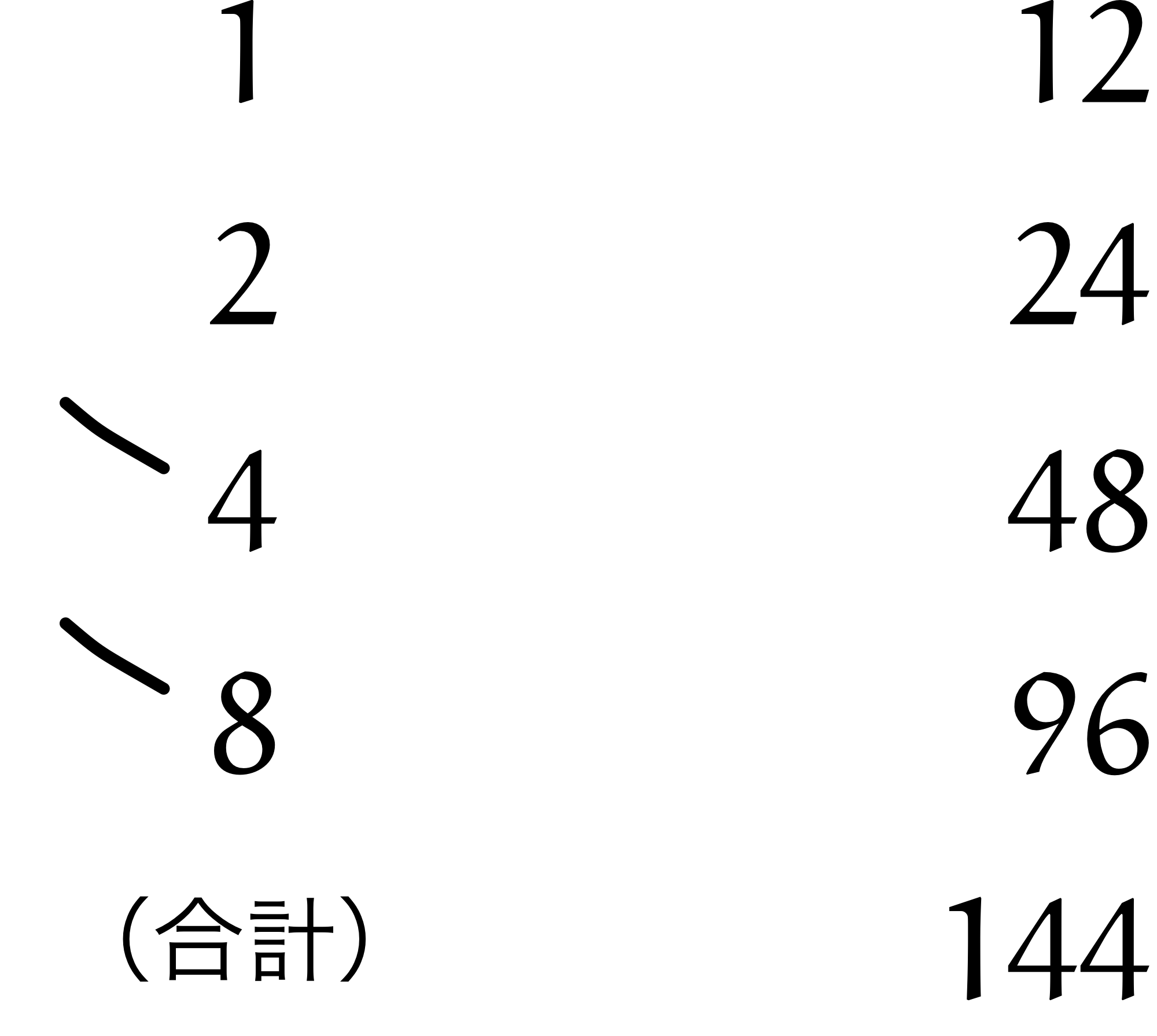
ユーリ「ははーん……さっきは $7$ を $1 + 2 + 4$ にしたじゃん? 今度は $12$ を $12 = 4 + 8$ にするんだよ、きっと! 使う数に印を付けてるの!」
僕「そうだね、それなら話が合うよ。式で書くとこういうことをしている」
$$ \begin{align*} & 12 \times 12 && \REMTEXT{これを計算したい} \\ &= 12 \times (4 + 8) && \REMTEXT{$12 = 4 + 8$だから($4$と$8$に印をつけておく)} \\ &= (12 \times 4) + (12 \times 8) && \REMTEXT{分配法則を使った} \\ &= 48 + 96 && \REMTEXT{乗算を行った} \\ &= 144 && \REMTEXT{印を付けた右側すべてを合計した} \\ \end{align*} $$
ユーリ「ややこしーけど、確かに掛け算になってるみたい。でも、こんなの、毎回うまくいくのかにゃあ?」
僕「……」
ユーリ「お兄ちゃん、どしたの? 次のパネルに行こうよ」
僕「わかったよ。完全にわかった。これは《二進法》になってる!」
ユーリ「は?」
僕「これ《二進法》なんだよ、ユーリ」
ユーリ「さっきは《十進法》って言ってなかった? 古代エジプトの人って《二進法》使ってたの?」
僕「いや、そういう意味じゃなくて、 このクイズに出てきた古代エジプトの掛け算は《二進法》で説明ができるってこと」
ユーリ「はあ」
僕「あのね。さっき僕たちは、 $7 = 1 + 2 + 4$ や $12 = 4 + 8$ という書き方をしたよね。 ここで使った、 $1,2,4,8,\ldots$ という数は、 $2^0,2^1,2^2,2^3,\ldots$ と書けるから、全部《$2$ の冪乗》だ」
ユーリ「にのべきじょう」
僕「たとえば、 $7$ はこうなるし…… $$ \begin{array}{ccccccccc} 7 &=& 1 &+& 2 &+& 4 & & \\ &=& 2^0 &+& 2^1 &+& 2^2 & & \\ \end{array} $$ ……それから、 $12$ はこう。 $$ \begin{array}{ccccccccc} 12 &=& 4 &+& 8 \\ &=& 2^2 &+& 2^3 \\ \end{array} $$ そうなるよね」
ユーリ「ふんふん、そりゃそーだね。そんで?」
僕「整数を《$2$ の冪乗》の和の形で表すっていうことは、《二進法》で表すのと同じことになる。 だから、どんな整数でも、さっきのクイズに出てきた古代エジプトの方法で掛け算ができるといえる」
ユーリ「ははーん……」
僕「$1 + 2 + 4$ じゃなくて、 $4 + 2 + 1$ のような逆順にすると、もっとよくわかる。 《$2$ の冪乗》のうち、どの数を使い、どの数を使わないかが、二進法の $1$ と $0$ にちょうど対応することになるからね」
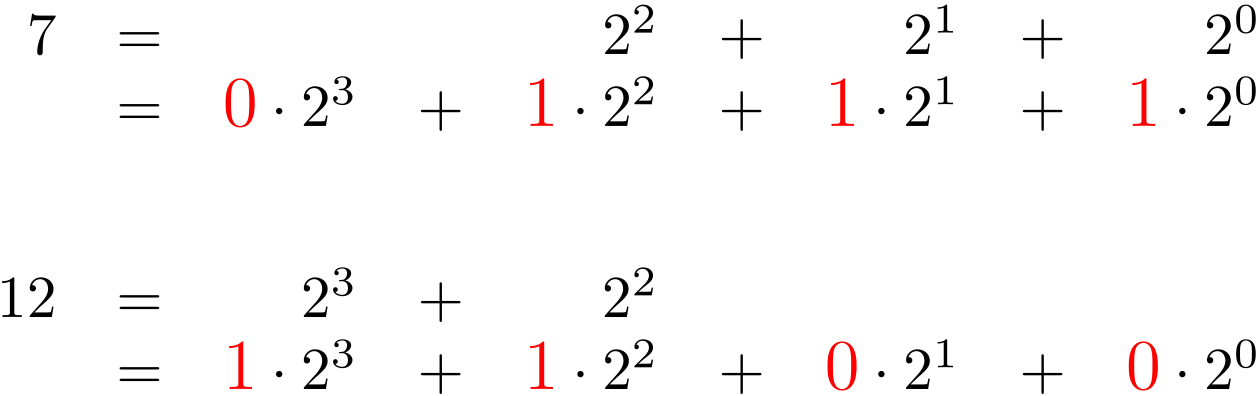
ユーリ「なーるほど! $7$ は $0111$ で、 $12$ は $1100$ ってこと?」
$$ \begin{array}{rcl} 7 &=& (0111)_2 \\ 12 &=& (1100)_2 \\ \end{array} $$僕「その通り! 一般的に書くと、こうだね」
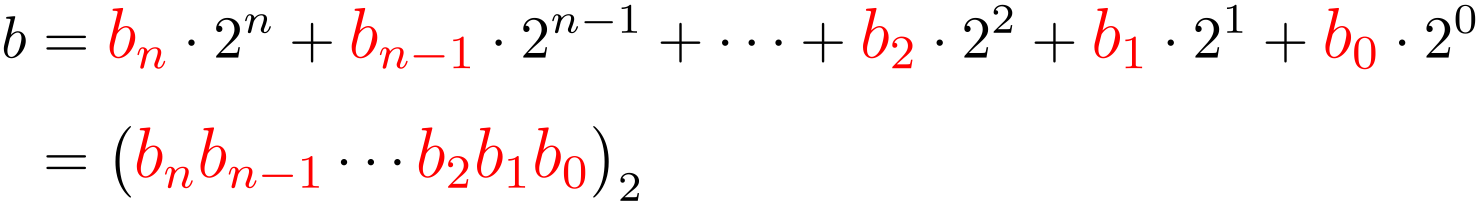
ユーリ「いきなり、ごちゃごちゃした」
僕「$b_n,b_{n-1},\ldots,b_0$ というのは、 $0$ か $1$ かを表しているとする。 《$2$ の冪乗》を足し合わせて $b$ を作るというのは、 $b_n,b_{n-1},\ldots,b_0$ のうち、どれを $0$ にしてどれを $1$ にするかを考えていることになるんだ。 つまり、整数を二進法で表記しているのと同じこと」
ユーリ「……わかった! わかりましたぜ、お兄ちゃん」
僕「つまり、このクイズに出てきた古代エジプトの掛け算では、 《数を $2$ 倍する》という計算と《数を足し合わせる》という計算を使って、掛け算を作り出していたんだね。 二進法が出てくるとは思わなかったなあ!」
ユーリ「ほんとだね! ……あれ?」
僕「何かおかしい?」
ユーリ「古代エジプトの話はいーけど、ユーリたちが掛け算するときは、どーなってんの? 二進法なんて使ってないよね」
僕「うん、僕たちは十進法を使っている。 筆算で掛け算するときを考えると……まず《九九を使って一桁同士の掛け算》はできる。 そして、《桁をずらす》ことで $10$ 倍の計算をしていることになるね」
ユーリ「えっと……」
注記
ヒエログリフ(聖刻文字、神聖文字)は公的な文字です。 縦書きも横書きもあり、左から右、右から左のどちら向きでも書くことができます。 ただし、書く向きに合わせて文字の形も反転します。
ヒエラティック(神官文字)は、ヒエログリフのくずし文字にあたります。
デモティック(民衆文字)は、後ほどヒエラティックに代わって使われました。
リンドパピルスはヒエラティックで書かれていますが、
本記事では参考文献(1)にならって、ヒエラティックをヒエログリフに直して示します。
ただし(1)とは異なり、現代の数の表記に合わせて左から右の向きに反転してあります。
本記事のヒエログリフは参考文献(1)をベースにして筆者(結城)が描きました。
文字の意味は参考文献によって大きく異なりますが、本記事では(2)の解釈に基づいています。
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 420本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第181回終わり)
(2017年1月13日)